Tijd is een modulair concept, een ordening modulo n waarbij n zowel a priori gekozen kan worden, als onbekend kan zijn. Een klok is geen machine maar een proces dat herhaaldelijk (“modulo n”) een spoor produceert dat gelijkaardig is (dezelfde waarde heeft) als voorgaande sporen en dat daardoor kan geteld worden. Dit is duidelijk waarneembaar bij de analoge klokken met wijzerplaat en (minstens) twee wijzers: een van de wijzers maakt een hele omwenteling en de andere wijzer telt het aantal omwentelingen van die eerste wijzer. Op een analoge klok telt de secondepositie de seconden, zestig seconden worden doorgegeven aan de minutenpositie en zestig minuten worden doorgegeven aan de urenpositie.
Rotatie is een modulair concept. Je kan dat zelf ervaren als je rond jouw as draait. Dan kan je het aantal rotaties tellen door hetzelfde (iets met dezelfde waarde als dat wat je gebruikt als referentiepunt) herhaaldelijk waar te nemen (herhaaldelijk betekent dus dat wat je waarneemt gelijkwaardig is met iets dat je al waargenomen hebt).
Tijd wordt dus geteld en dat is discontinu. Een tijdreeks is 1, 2, 3, enz… dus “tussen” de verschillende stappen is er niets geteld, wat er “dan” (tussen twee stappen) zou gebeuren is hypothetisch en we kunnen gerust veronderstellen dat dit continu is of andere eigenschappen heeft want die veronderstelling is irrelevant voor het concept zelf. Dit heeft praktische gevolgen als men zonder kritische houding uitgaat van het a priori van continuïteit. Continuïteit is immers operationeel niet te realiseren (als toestanden die elkaar uitsluiten waartussen een verschil kan gemaakt worden) en dat betekent dat het eigenlijk een constructie is (“indien…, dan...”). Als men op basis van twee metingen ervan uitgaat dat er datapunten kunnen geanticipeerd worden “tussen” deze twee (met een lineair verband of niet, minimaal dus een differentieerbaar verband) dan veronderstelt men een continuïteit die misschien niet waarneembaar is, men veronderstelt punten waartussen een agens een verschil kan maken terwijl dat in werkelijkheid niet zo is, hypothese die misschien zal leiden tot waarnemingsparadoxen. Door discontinu sporen te tellen houden we dus rekening met de waarnemingsgevoeligheden of waarneming resoluties van agentia-in-context. De continuïteit-discontinuïteit verschil is goed te modelleren door een rotatie, door een frequentie van zekerheid.
Tijd wordt ook telbaar bij een digitale klok die geen omwentelingen telt maar de meest primitieve overgang tussen een laagbit en een hoogbit. Na een laagbit volgt een hoogbit en dan terug een laagbit. Als we dit willen tellen dan moeten we een van de bits als referentie kiezen en als de referentie voor de tweede maal waargenomen wordt kunnen dat markeren met een tweede bit (de “carry bit”). Dan hebben we twee bits die kunnen doorlopen worden. Die twee bits geven ons vervolgens “een grotere wijzerplaat” en als we die grotere wijzerplaat doorlopen hebben, hebben we nood aan een derde bit om dat te kunnen markeren. In dit binair systeem telt de eerste bit een een of geen, twee worden doorgegeven aan de tweede bit, vier worden doorgegeven aan de derde bit, acht worden doorgegeven aan de vierde bit, enzovoort. In het proces wordt “de wijzerplaat” op een exponentiële manier steeds groter. Dit is niet anders dan een proces dat gehele getallen geneert en ze in een positiesysteem representeert die gebaseerd is op exponenten van grondtallen. Het enige grondtal dat niet kan gebruikt worden is het getal 1.
Tijd kunnen we dus kwantificeren door een proces herhaaldelijk te doorlopen. Tijd wordt geteld. Herhaling maakt vergelijking mogelijk ten opzichte van een vrij te kiezen referentie. De actie die te herhalen is genereert voor elke betrokkene een eigen klok met een eigen verdubbelingstijd of halveringstijd van “het verschil dat een verschil maakt”. Elk proces dat sporen achterlaat waarvan het aantal alleen maar toeneemt (of alleen maar afneemt) is een klok en als we de sporen tellen meten we tijd. Dit betekent dat er niets absoluuts is aan een klok. “Uitsluitend monotoon toenemen” (monotoon afnemen) betekent ook dat dat proces irreversibel is. Deze eigenschap (één referentieproces van toename of afname) zorgt er juist voor dat we andere processen kunnen ordenen. Ordening is fundamenteel in de structuur van de werkelijkheid. Ordening is iets anders dan willekeurigheid. Tijd is de abstractie die voor ordening zorgt.
De manier van tijd meten vereist dat de referentietoestand die geteld wordt een andere toestand uitsluit, dan pas kan er geteld worden. In een proces zijn er daarenboven ook simultane gebeurtenissen omdat we elk proces kunnen modelleren als een causale koppeling (een netwerk) van buffers (anders zouden we niet van een proces spreken). Cumulaties (dus de intensiteit van buffers) kunnen toenemen (accumuleren) of afnemen (decumuleren), de tijd kan enkel toenemen en dit is een noodzakelijke voorwaarde om het afnemen en toenemen van iets anders (bijvoorbeeld een buffer) te kunnen waarnemen. We kiezen er voor om de tijdsparameter die we moeten construeren met behulp van een proces enkel te laten toenemen en dat we kunnen gebruiken om de toename en afname van de buffers te ordenen. Deze ordening is de ordening van de processtappen. We laten ons daarom leiden door de inzichten van de systeem dynamica om de tijd in een willekeurig proces af te leiden van de processtappen (eigenwaarde, verdubbeling, halvering enz...). De buffers zijn de Maxwell duiveltjes die voor ordening (en dus tijd) zorgen: zij bepalen de mogelijkheid van causale koppeling (de irreversibele acties) in het proces. Een mooi voorbeeld hiervan zijn katalysatoren: door een katalysator toe te voegen aan een reactieomgeving kunnen we de reactie in een specifieke richting sturen (en dus is die reactie dan niet een willekeurig maar een geordend proces).
Het meest eenvoudige model van een netwerk is een model met twee knooppunten, noem ze de atomen (toestanden) p en q en afgeleide (verbinding) p•q (een 1-splitsing). De meest eenvoudige 1-splitsing is dan het meest primitieve meetinstrument voor tijd: het gedrag of proces van trillen, het repetitief schakelen tussen slechts twee elkaar uitsluitende toestanden die een spoor achterlaten. We modelleren dit onder andere als de logische oscillatie tussen een projector en een welgevormde haakuitdrukking.
Het meest universele universum is er een met vier mogelijk toestanden, noem ze de atomen a1, a2, a3 en a4. Elk universum kan zo voorgesteld worden, wat betekent dat er een schaal is waarop dit mogelijk is. Drie verschillen van toestanden met dezelfde (vierde) toestand als referentie (en dus drie eenheden a1-a4, a2-a4, a3-a4) kunnen een evenwicht modelleren. Evenwicht en dus een willekeurig referentiepunt is onvermijdelijk. Dat evenwicht is dus onafhankelijk van de de grootte van het universum (en dus de schaal). De lokale schaal van het universum kunnen we construeren door een som van positieve getallen (som die nooit nul zal zijn).
We kunnen altijd veronderstellen dat een proces, “de sporen producerende klok”, in parallel loopt met een ander proces, in disjunctie dus, beide processen zijn dan invariant voor elkaar maar zijn voor een aantal aspecten niet onafhankelijk van elkaar. Het Lorentz nulpunt dat we modelleerden bij het onderzoek van het “geschaalde” verschil, de verhouding (a1-a4)/(a1+a4), toont dat onafhankelijkheid een geïdealiseerde vooronderstelling is, aan een Lorentz invariant valt niet te ontsnappen.
De voorstelling van een netwerk met buffers met minimale en maximale capaciteit toont eveneens aan dat begrenzing onvermijdelijk is.
We hebben dus niet veel meer nodig dan die fundamentele inzichten om sporen in de tijd te kunnen ordenen.
Veronderstel nu een willekeurig proces. We onderscheiden hierin n toestanden met dezelfde waarde <<>> (allemaal verschillend van de toestand die nu ervaren is met waarde <>), en elk met een intensiteit. We noemen ze daarom n simultane intensiteiten van m buffers, de buffers zijn de m entiteiten die een gedrag kunnen vertonen dat waarneembaar is door de veranderende intensiteit van elk van de buffers. De n toestanden sluiten elkaar twee-aan-twee uit (per definitie van toestand) en sluiten ook de toestand nu uit (die vier mogelijke representaties heeft: a1, a2, a3 en a4). Daarenboven veronderstellen we nu dat die toestanden causaal met elkaar gerelateerd zijn zonder dat er a priori enige notie van tijd aan causaliteit verbonden is. Tijd leiden we af van causaliteit en niet omgekeerd. Dus het gedrag van sommige buffers is niet onafhankelijk van het gedrag van sommige andere buffers (ze zijn gekoppeld en we willen die koppeling logisch representeren en metrisch kwantificeren). Om intensiteiten te kunnen tellen moeten we dan een getal G veronderstellen dat bepaald wordt door de volledige logische configuratie (“indien…, dan...”) en niet alleen door één simultaneïteitsinterval (zoals bij een processnelheid) die de mogelijke intensiteiten kan geven van één buffer. Het getal G modelleert dan de resolutie van het hele proces. Verschillende getallen gm/G (een verhouding die per definitie groter is dan nul en kleiner dan 1) interpreteren we als de eigenwaarde van de m-de buffer in de configuratie. Dit kunnen we als volgt preciezer beschrijven. Neem twee buffers b1 en b2. Op een bepaalde stap in het proces stellen we vast dat de intensiteit van beide bijvoorbeeld gelijk is (dank zij de transformatie (“gelijkheid”) tussen de getallen die de gezamenlijke eenheid weergeeft). Stel dan dat het nog niet voorgekomen is dat de intensiteit van b2 kleiner is dan de intensiteit van b1. Er bestaat tussen beide dus een strikte ordening die op een bepaalde stap van het proces niet meer waarneembaar is (de intensiteiten zijn dan dezelfde, het verschil is gelijk aan nul). We interpreteren dat als de gelijkheid van output van buffer 1 en input van buffer 2 (of omgekeerd). Hoe doen we dat? We vergelijken de m intensiteiten (dus van de buffers b1, b2, … bm) twee-aan-twee bij stap n in het proces met de m intensiteiten twee-aan-twee bij stap n+1 in het proces. Enkel als de intensiteiten gelijk zijn hebben we een mogelijke koppeling en dan gebruiken we dat om te controleren of bij de voorbije stappen de intensiteit van een van beide niet groter was. We moeten dat in twee richtingen doen want het zou kunnen zijn dat beide buffers met elkaar gerelateerd zijn doordat in het proces de intensiteit van de ene toeneemt als de intensiteit van de andere afneemt en omgekeerd. Het zou kunnen zijn dat we een dynamisch evenwicht aan het onderzoeken zijn. Daarenboven moeten we ook rekening houden met de beperkingen van elke buffer: zijn maximale capaciteit (de maximale intensiteit die dus ook een minimale intensiteit veronderstelt). De maximale intensiteit is bereikt als de ordening van intensiteiten niet meer mogelijk is, verschillen van intensiteit wordt in die buffer dan niet meer waargenomen. Dat kan bijvoorbeeld ook betekenen dat de buffer als entiteit uit het proces verdwenen is (en er bijvoorbeeld enkel maar een katalytische functie heeft). Als gevolg daarvan is het onvermijdelijk dat we altijd twee speciale buffers zullen vinden: een bron (een input in het proces die niet vermindert van intensiteit en niet verdwijnt, wat we meten is altijd gelijk) en een put (een output in het proces die niet vermeerdert van intensiteit en niet verdwijnt, wat we meten is altijd gelijk).
Omdat we een twee-aan-twee vergelijking maken kunnen we matrix technieken gebruiken omdat een matrix een structuur is die een twee-aan-twee relatie kan kwantificeren. Een individuele cel mij van een m*m matrix kan de gerichte koppeling representeren van een buffer mi met buffer mj. Om een tijdsparameter te construeren met getallen benutten we nu de lineariteit en idempotentie die mogelijk is bij een geschikte selectie van binaire operaties. Dus moeten we eenheden veronderstellen die projectoren zijn in een vastliggend universum (dus dubbelgetallen van het type (x-x0) die met hun intensiteiten gemodelleerd worden). Voor g1 en g2 reële getallen van het meest universele type 1/(1±k) als eenheid, met intensiteit een exponent, blijkt een geschikte selectie van binaire operaties de volgende twee: max(g1, g2) (of min(g1, g2)) voor de idempotente eenheid, gecombineerd met een som operatie voor de exponent. Is het ene extremum een min(g1, g2), dan is het andere extremum een max(g1, g2). Op die manier modelleren we onze waarnemingsresolutie. Bijvoorbeeld: elke operatie op een intensiteit groter dan het maximum zal hetzelfde resultaat hebben (steady state) en dan gaat de ordening verloren. Dit is de operationele betekenis van “invariantie”, “idempotentie” en “oneindig” in een onvermijdelijk beperkt universum: zeer groot en onwaarneembaar groter, zoals bij een weegschaal met maximum 5 kg waar alle gewichten hoger dan 5 Kg niet meer kunnen geordend worden door de meting ervan met behulp van die weegschaal (voor deze operatie uitgevoerd door een agens-in-context is dus 5 niet anders dan oneindig, genoteerd ∞, in die context) en waarbij er ook een ondergrens is voor een gewicht dat die weegschaal kan beïnvloeden. We zullen verder zien hoe we ±∞ in het model kunnen gebruiken.
Vertaald in de matrix techniek met getallen verschillend van ±1 betekent dit dat het getalproduct van matrixcellen vervangen wordt door een getalsom en een getalsom van de producten vervangen wordt door een max(., .) operatie (of min(., .) operatie). Door deze keuze worden ofwel monotoon grotere getallen bereikt bij elke stap of monotoon kleinere getallen en deze getallen hebben dus alle karakteristieken van “tijd” (de strikt stijgende of dalende parameter die ons de mogelijkheid geeft om veranderingen te ordenen). Dus elk proces, dat op die manier met buffers in dynamisch evenwicht beschreven wordt, gedraagt zich als een klok die gekarakteriseerd wordt door processtappen. De stappen bepalen de toestanden (die elkaar dus uitsluiten) en dus de resolutie. De sporen van de klok worden per processtap gegenereerd, zij sluiten elkaar uit. Het verdubbelen of halveren van de intensiteit van de sporen meet “tijd” voor dit proces.
De vervanging van een product van getallen door een som betekent impliciet dat exponenten gesommeerd worden en dat is dan volledig compatibel met het inzicht dat de intensiteit van de projector van een atoom een macht is van 2 (en dus ook een macht is van gelijk welk grondtal verschillend van 2 en verschillend van 1) en daarenboven dat elk atoom in twee onderscheidingen kan voorgesteld worden.
De veronderstelling van idempotentie en lineariteit bij de modellering impliceert dus dat er een matrix Aij te vinden is die bij elke stap n de transformatie uitvoert van een vector met m componenten (a1(n)(x1-x10), a2(n)(x2-x20), …, am(n)(xm-xm0)) naar een andere vector (a1(n+1)(x1-x10), a2(n+1)(x2-x20), …, am(n+1)(xm-xm0)) met m componenten, voor een specifieke selectie van operaties.
Neem nu de eerste component van de vector, a1(n)(x1-x10). De getallen aindex zijn de intensiteit van de buffers met eenheid (xindex-xindex(indexn)) voor elke processtap (de stappen in een proces sluiten elkaar uit maar de intensiteiten van de buffers veranderen simultaan). De eenheden in de buffers zijn de (minimale of maximale) verschillen met xindex. De processtappen worden gegeven door de opeenvolgende getallen n. Een netwerk van gekoppelde buffers (met knooppunten waar mogelijk meerdere bogen samenkomen) wordt dan voorgesteld door de matrix Aij. Die matrix moeten we begrijpen als patroon. Inderdaad: in de lineaire algebra is bekend dat matrices Aij en Bij, alhoewel verschillend, toch gelijkvormig kunnen zijn, namelijk hetzelfde spectrum van eigenwaarden kunnen hebben. Dat patroon kan een logische structuur coderen in een vastliggend onderscheidingen universum (de klassieke hypothese). Het aantal rijen (kolommen) van de matrix kunnen we zo groot nemen als het aantal buffers die we modelleren (in het voorbeeld is dit m). De getallen aii kunnen dan geïnterpreteerd worden als een bijkomende intensiteit eigen aan de buffer ai los van enige verbinding met andere buffers. Dit is dus de eigenwaarde van de eigenvector die de buffer representeert. De eigenwaarde wordt door het aspect processtap gekwantificeerd door een “verdubbelingstijd” of “halveringstijd”. Dit is ondubbelzinnig waarneembaar voor een buffer waarvan het gedrag is dat het iets telbaar als spoor van activiteit produceert, de buffer doet dat repetitief en gedraagt zich dus als een klok.
De telbaarheid is onvermijdelijk gerelateerd met discontinue veranderingen (“indien..., dan..., zoniet...”): pas als een bepaalde grens overschreden is zal een exponentieel toenemende of afnemende verandering een waarneembaar spoor achterlaten. De telbaarheid is onvermijdelijk gerelateerd met de mogelijkheden van waarnemen door een agens-in-context. Elk getal als spoor kwantificeert de laatst toegevoegde onderscheiding, de laatst toegevoegde onderscheiding moet niet als “iets” begrepen worden maar als een (niet te kiezen) aspect van gedrag dat een spoor achterlaat in de buffer gekwantificeerd op stap n voor m buffers als (a1(n)(x1-x10), a2(n)(x2-x20), …, am(n)(xm-xm0)). Voor die getallen kunnen verschillende keuzen gemaakt worden die daardoor onvermijdelijk gerelateerd zijn aan een schaal. Een schaal kunnen we vaststellen als we “hetzelfde” op een andere manier kunnen meten (schalen delen dezelfde waarde). We tonen aan dat deze getallen onvermijdelijk exponenten zijn van een onbekende eenheid, getallen die ook nog eens genormaliseerd worden bij elke stap in het proces. Dus Aii is eigenlijk een m×m matrix die inwerkt op een vector (exp(y10), exp(y20), … exp(ym0))T. De exponenten zijn het resultaat van de processtappen en we vinden in de exponenten ook de “ladingen” die nodig zijn om de processen te laten interageren in dezelfde buffer. Inderdaad: normalisatie is nodig als we interacties van positieve (1+k) en negatieve feedback (1-k) willen modelleren die elkaar in dezelfde buffer kunnen opheffen en de normalisatie kunnen we altijd uitvoeren met twee positieve getallen (die we in deze context kunnen interpreteren als de minimum intensiteit (verschil) en de maximum intensiteit (som) van een buffer). Positieve getallen kunnen we altijd voorstellen als kwadraten. Bijvoorbeeld bij de keuze (p+q) versus (p-q) wordt de normaliserende relatie: (p+q)n(p-q)n(p2-q2)-n = 1. Hierbij kan p niet gelijk zijn aan q, we veronderstellen daarom p groter dan q. Delen door p geeft het patroon (1+q/p)n(1-q/p)n(12-(q/p)2)-n = 1. Stel q/p=k. Stel 1+k=r en 1-k=s dan zijn de twee genormaliseerde intensiteiten voor te stellen als de verhoudingen rn(rs)-tn en sn(rs)-(1-t)n. Hierin is t de lading van de normalisatie en de waarde van t bepaalt of een positieve feedback, negatieve feedback of stabiele toestand gemodelleerd wordt. Uiteraard geldt rn(rs)-tnsn(rs)-(1-t)n=1. Deze laatste relatie maakt duidelijk dat alle variabelen (stap n en lading t) zich in de exponenten bevinden als r en s constanten zijn (een vaste eigenwaarde k) voor een bepaalde buffer. Uit 1+k=r en 1-k=s leiden we af dat k=(r-s)/2, en dit is niet anders dan k=(r-s)/(r+s). Dit interpreteren we als volgt: de eenheid van de buffer is de reciproque som 1/(r+s) en dit is de lokale schaalfactor. De intensiteit van de eenheid is het verschil (r-s), dus: k als het product (intensiteit)×(eenheid) is genoteerd als (r-s)×(1/(r+s)). De eigenwaarde is minimaal voor r=s (er is dan geen interval, k=0) en maximaal voor s=0 (er is dan evenmin een interval, k=1). De eigenwaarde k wordt dus niet rechtstreeks gemeten maar wordt berekend uit de verdubbelingstijd of halveringstijd in het proces ten opzichte van een andere klok. Dit maakt ook duidelijk dat er niets absoluuts is aan een klok, twee systemen van interagerende buffers kunnen als klok voor elkaar gebruikt worden en klokken kunnen we rondom ons ontdekken (typisch als een mogelijk spontaan proces) maar ook zelf ontwerpen (typisch als een stuurbaar proces). Elke klok is een proces dat sporen achterlaat.
Dat patroon zal dus gelden voor elke buffer afzonderlijk en is dus een functie van twee getallen, een r (=1+k) en een s (=1-k). Een operatie die enkel sommen maakt en genormaliseerd wordt door de keuze van ofwel min(som) ofwel max(som) zal een éénduidige ordening vertonen in de factor (1/(r+s)). Deze operator heeft een invariante eenheid (idempotentie). Dankzij die duidelijke strikte ordening van enkel toenemende processtappen kunnen alle verschillen van getallen (we meten Δ) modelleren hoe de intensiteiten van individuele buffers veranderen. Een stabiel netwerk van gekoppelde buffers (knooppunten) wordt dan minimaal voorgesteld door een matrix Aij en zijn spectrum van eigenwaarden. Verschillen zijn altijd onafhankelijk van een referentie en dit verklaart waarom matrices Aij en Bij gelijkvormig kunnen zijn. De maximum intensiteit van een buffer kan de rol spelen van onveranderlijke referentie (de buffer kan maar zo intens zijn als zijn maximale capaciteit) en zo wordt de “maximaal gevulde” buffer een stabiele toestand (steady state) in het netwerk (en alhoewel aanwezig en essentieel, is de buffer in zijn “steady state” toch “onzichtbaar” voor verandering, zoals het getal 1 onzichtbaar is voor het getalproduct). De getallen aij die voorgesteld worden in de matrixcellen worden dan geïnterpreteerd als de intensiteit van de causale koppeling tussen buffer ai en buffer aj. Het getal aij kan verschillen van het getal aji omdat de causaliteit uiteraard ofwel een noodzakelijke voorwaarde, ofwel een voldoende voorwaarde kan zijn. Dit is niet anders dan de notering voor de zin in een interval en we kunnen ons dat voorstellen als de zin van de koppeling in de graaf die de koppelingen in een netwerk kan voorstellen.
Wat nog niet gemodelleerd werd is de productie zelf van sporen (want voor een betrouwbare klok mag de productie van sporen de interne dynamiek niet beïnvloeden). Dit model volgt en we zullen begrijpen hoe we hiermee een bron en een put kunnen modelleren als essentiële buffers in elk causaal netwerk in werkelijkheid. Want wat ook nog niet gemodelleerd werd is dat buffers die noch bron noch put zijn begrensd zijn in hun minimale en maximale intensiteit. Blijkbaar hebben we die praktische modellering niet nodig om de abstractie “tijd” in het haakformallisme te representeren.
Wat we tot nu toe theoretisch begrepen hebben kunnen we met het meest eenvoudige voorbeeld illustreren: een netwerk met maar twee buffers.
We veronderstellen een 2×2 matrix A, soms genoteerd als [aij]. We zullen A noteren als (a11, a12; a21, a22). A opereert op een vector x, genoteerd als kolomvector (x10, x20)T bij de start. Het resultaat van de inwerking is (x11, x21)T enz…. De vector die bereikt werd wanneer de n-de operatie uitgevoerd zal worden is (x1n, x2n)T. (x1n, x2n)T is de transpose van de rijvector (x1n, x2n). De zes getallen zijn de exponenten van een eenheid per vectorcomponent die niet gekend is maar onvermijdelijk verschillend is van 1, dus met het patroon (1±k). Dit modelleert het onbekende kwantum “iets” dat verdeeld is over de buffers en op een bepaalde stap in de evolutie een intensiteit in een buffer bereikt. Dus A is eigenlijk de 2×2 matrix (exp(a11), exp(a12); exp(a21), exp(a22)) die inwerkt op een vector (exp(x10), exp(x20))T. We hebben de exponentiële functie gebruikt in deze voorstelling, maar in het algemeen kunnen we gelijk welke voorstelling gebruiken met het patroon (1±k)m (met 0<k<1) waarbij het grondgetal 0 en het grondtal 2 dan limietvormen zijn. Het voordeel van het gebruik van verschillende grondtallen is dat de exponent voor alle componenten van de kolomvector dezelfde kan zijn: een aantal processtappen. Het voordeel van het gebruiken van het grondtal e is dat het modelleert dat er een gemeenschappelijk “iets” kan zijn dat verdeeld is over de buffers en dus daar een andere exponent krijgt als intensiteit.
Het gevolg hiervan is dat de operatie die de inwerking modelleert van de matrix A op de vector x (een product) als een som kan genoteerd worden van de exponenten en dat zijn de vier getallen in (a11, a12; a21, a22) en de twee getallen in (x10, x20)T. De evolutie na n-1 stappen noteren we dan als (x1n, x2n)T. Dus (x1n, x2n)T is een andere notering voor (a1(n)(x1-x10), a2(n)(x2-x20)) die de intensiteit en de eenheid expliciteert, die op zijn beurt een andere notering is van (log(1±k1)(1±k1)x1n), log(1±k2)(1±k2)x2n)) waarbij de eenheden (1±km) verschillend zijn van 1.
De getalsom “neemt dus de plaats in” van het klassiek getalproduct van een matrix term en een vector term (deel van het matrixproduct). Deze uitspraak klinkt exotischer dan nodig want dit is een techniek die in het wiskundig onderzoek beschikbaar is. Dit is het rechtstreeks gevolg van het feit dat het enige dat we kunnen waarnemen is: na n stappen nemen we een tweede spoor van gedrag waar, er is een verdubbeling van het spoor. Het spoor is de soort die discontinu geteld wordt en is dus een invariant voor het proces. Stel dat we één spoor waarnemen, dan kunnen we wel stappen tellen met behulp van die klok, maar we kunnen geen sporen tellen tussen de waarneming van een eerste spoor en de waarneming van een tweede spoor. De operatie die we willen modelleren is de toevoeging van “de laatst toegevoegde onderscheiding” die dezelfde waarde heeft als alle andere onderscheidingen (die dezelfde rol speelt in de operatie) en als exponent hebben we daarvoor een vrije keuze. Elke keuze zal een ander grondgetal genereren. Omdat we nu enkel spontaan gedrag willen modelleren (dat wat blijkt te gebeuren als we iets kiezen) nemen we daarvoor altijd hetzelfde: het maximum van de gemaakte sommen. Hiermee kunnen we immers uitdrukken dat al die sommen in deze toestand simultaan en dus evenwaardig zijn (een maximaal getal impliceert een getal dat kleiner is zowel voor som als product) en de machtsverheffing met zijn twee soorten inversen modelleert het creatief product in het getallen domein en het gedrag is de verandering in het (momenteel) grootste onderscheidingen universum dat enkel nu blijkt te gebeuren en dat we alleen maar kunnen laten gebeuren. We kiezen voor een maximum omdat de buffers een maximale capaciteit hebben van de in principe onbekende eenheid (aspect of “deel” van de onbekende eenheid die het geheel van buffers modelleert).
Dus het resultaat van de operatie van de matrix (a11, a12; a21, a22) op de vector (x10, x20)T is de vector: (max(a11+x10, a12+x20), max(a21+x10, a22+x20))T. De klassieke getalsom van de producten (die gebruikt wordt bij een klassiek matrix product) vervangen we dus door de selectie van het maximum van de sommen (die de plaats innemen van het klassieke getalproduct). Door deze selectie wordt dus een onbekende eenheid van het type (1±km) gemodelleerd die de intensiteit na één stap geeft met eigenwaarde ±km van een vector component (xm-xm0) die verschilt van nul. Dit getal is een lineaire functie van alle getallen (de componenten van de matrix en de componenten van de vector).
Dit wordt nog duidelijker met behulp van een concreet voorbeeld met getallen: we veronderstellen een 2×2 matrix A als (1, 8; 2, 3) die inwerkt op een vector x, genoteerd als kolomvector waarbij we de evolutie starten bij x(0)=(1, 0)T. De parameter die we volgen is de stap en dus na n stappen bereiken we x(n). De eerste stap na de start is te berekenen als x(1)=(max(1+1, 8+0), max(2+1, 3+0))T=(8, 3)T. De stap daarna is x(2)=(max(1+8, 8+3), max(2+8, 3+3))T=(11, 10)T . De stap daarna is x(3)=(max(1+11, 8+10), max(2+11, 3+10))T=(18, 13)T enzovoort.
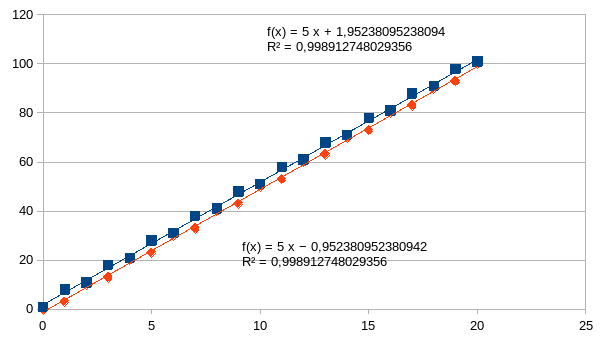
De volgende grafiek geeft de intensiteit van de twee componenten van de vector in de loop van de evolutie van 20 stappen.

De stappen zijn uiteraard discontinu. De intensiteiten liggen niet op één lijn, maar om de twee stappen is een patroon te herkennen. De toename van de intensiteit van beide vectorcomponenten vertoont immers een patroon dat door de richtingscoëfficiënt van de berekende en benaderende rechte kan gekwantificeerd worden (de twee relaties f(x) in de grafiek) en die in dit geval gelijk is aan +5 en dat voor de intensiteit van beide vectorcomponenten.
We zien de intensiteiten van twee gekoppelde buffers bij elke processtap n, en dat voor 20 stappen. De intensiteiten nemen enkel toe zoals we verwachten bij een betrouwbare klok. We zien de abstractie van de klok hier geïllustreerd als het onbeperkt kunnen toenemen van deze intensiteiten. Het verschil tussen de intensiteiten van beide buffers wisselt tussen 1 en 5. Die intensiteiten zijn verdubbelingstijden waaruit de eigenwaarde kan berekend worden van het proces dat doorgaat in een van de buffers en dat proces is de productie van een spoor dat een noodzakelijke voorwaarde is voor een proces dat doorgaat in de andere buffer (en dus is het proces dat doorgaat in die andere buffer een voldoende voorwaarde voor de aanwezigheid van dat spoor). De richtingscoëfficiënt is de berekende intensiteit van de opeenvolging van de intensiteiten, namelijk de parameter “stap” in x(stap)=(max(a+b, c+d), max(e+f, g+h))T. Voor de parameter “stap” gebruiken we een andere klok, wat betekent dat we altijd twee klokken met elkaar relateren. We zijn er nu in geslaagd, niet alleen om twee processen te veronderstellen, maar twee betrouwbare klokken die beide monotoon gedrag (toename of afname van sporen) vertonen. Zij kunnen dus elkaar vervangen ondanks het feit dat ze een andere eigenwaarde hebben. Dit betekent dat beide processen sporen produceren die betrouwbaar te anticiperen zijn, we moeten geen van beide processen effectief doorlopen. In het meest algemene geval zal er immers ook altijd iets anders gebeuren en dat is niet te anticiperen. Dus minstens twee klokken geven ons de mogelijkheid om te modelleren wat er wel te anticiperen is als niet alles kan geanticipeerd worden. Dit is het gevolg van een invariante relatie tussen alle interne knooppunten van een proces, knooppunten die door causale relaties verbonden zijn. We hebben dus twee processen gesynchroniseerd zonder ruimtelijke intuïties nodig te hebben (zoals dat wel nodig is in de klassieke relativiteitstheorie).
Een herhaald uitgevoerde operatie geeft een intensiteit aan de eenheid die herhaald wordt. We berekenen daarom A2 op dezelfde manier, dat betekent: met dezelfde selectie van operaties. A2 is (1, 8; 2, 3)(1, 8; 2, 3)=(max(1+1, 8+2), max(1+8, 8+3); max(2+1, 3+2), max (2+8, 3+3))=(10, 11; 5, 10) wat duidelijk maakt dat x(2)=A2(1,0)T. Door inductie is het duidelijk dat het niet anders kan dat x(n)=An(1,0)T. De intensiteit van de eenheid A zien we dus ook hier in de exponent. We kunnen het resultaat dus noteren als (x11, x21)T=A(x10, x20)T en meer algemeen (x1(n+1), x2(n+1))T=A(x1n, x2n)T en er geldt ook dat (x1(n+1), x2(n+1))T=An+1(x10, x20)T.
Dit betekent dat alle sporen van het proces voor gelijk welke stap te anticiperen zijn op voorwaarde dat A een invariante matrix is, die dus een invariante relatie tussen buffers modelleert. Met een invariante matrix A (waarmee we de causale koppeling tussen intensiteiten van entiteiten (buffers) modelleerden) hebben we dus ook een betrouwbare klok gemodelleerd die enkel maar toenemende intensiteiten vertoont voor de parameter “stap”. De reciproque zal dan enkel maar afnemende intensiteiten modelleren.
Maar enkel afnemende intensiteiten worden ook gemodelleerd door de duale invulling van matrix A in combinatie met de operatie “minimum”. Ook dit wordt duidelijker met behulp van getallen: we veronderstellen de 2×2 matrix -A als (-1, -8; -2, -3) die inwerkt op een vector x, genoteerd als kolomvector waarbij we de evolutie starten bij x(0)=(1, 0)T. De volgende stap is x(1)=(min(-1+1, -8+0), min(-2+1, -3+0))T=(-8, -3)T. De stap daarna is x(2)=(min(-1-8, -8-3), min(-2-8, -3-3))T=(-11, -10)T . De stap daarna is x(3)=(min(-1-11, -8-10), min(-2-11, -3-10))T=(-18, -13)T enzovoort. Het is duidelijk dat de grafiek de richtingscoëfficiënt -5 zal hebben. We tonen de grafiek met een startsituatie x(0)=(20, 19)T wat onmiddellijk duidelijk maakt wat door het snijpunt met de ordinaat gemodelleerd wordt.
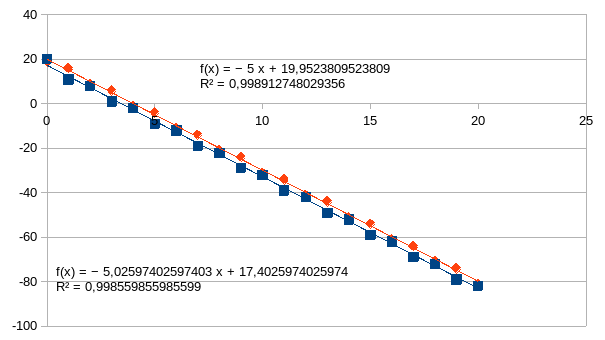
We berekenen nu (-A)2 op dezelfde manier, dat betekent: met dezelfde selectie van operaties. (-A)2 is (-1, -8; -2, -3)(-1, -8; -2, -3)=(min(-1-1, -8-2), min(-1-8, -8-3); min(-2-1, -3-2), min(-2-8, -3-3))=(-10, -11; -5, -10) wat duidelijk maakt dat x(2)=(-A)2(1,0)T. Het is duidelijk dat het niet anders kan dat x(n)=(-A)n(1,0)T.
Elk proces gedraagt zich als een klok die gekarakteriseerd wordt door processtappen die discontinu een spoor produceren. De stappen bepalen de toestanden (die elkaar dus uitsluiten) en dus de resolutie. De sporen van de klok worden per processtap gegenereerd, zij sluiten elkaar uit. Het verdubbelen of halveren van de intensiteit van de sporen meet “tijd” voor dit proces. De relevante tijdstap (globaal, k=1 en lokaal, k=k) wordt dus afgeleid vanuit het waarnemen van (elkaar uitsluitende) toestanden (van en door entiteiten die agentia zijn) in het proces en wordt niet a priori geponeerd. We tellen de toestanden discontinu.
Bij ons algemeen onderzoek naar processen met één eenheid hebben we de waarden op de abscis geïnterpreteerd als tijdstappen. Dat is een eenvoudige conventie, maar slechts een conventie. Er is geen enkele reden om daar een diepere betekenis aan te geven. We kunnen evenzeer de waarden op de ordinaat als stappen gebruiken zodanig dat ze als de waarneembare stappen in intensiteit kunnen geïnterpreteerd worden (en dus als verschillen die een verschil maken voor het agens-in-context), we zouden exact dezelfde curve bekomen met datapunten die de relatie geven tussen abscis en ordinaat. Maar helemaal verhelderend is het om daarenboven ook de eenheid op de assen te transformeren zodanig dat de intensiteiten lineair kunnen gerepresenteerd worden, de eenheid van de intensiteiten verandert dan niet. Dus: in plaats van de waarden te interpreteren als bijvoorbeeld m×1=(1±k)n×1 met n lineair op de abscis, en 1 de eenheid op de as, kunnen we, na de één-op-één transformatie, ook schrijven logm+log1=nlog(1±k)+log1 en dus n=logm/log(1±k). Dat kunnen we voorstellen met m (de intensiteit op stap n) lineair op de abscis. Lineaire toenames zijn gemakkelijker te interpreteren en we hopen dan dat dit het inzicht illustreert dat er niets “speciaal” is aan tijd. Tijd is een mogelijke vrijheidsgraad zoals de intensiteit van een proces een mogelijke vrijheidsgraad is. De abscis geeft dan de (lineaire) intensiteit en de ordinaat geeft dan de overeenkomstige processtap n (het “tijdstip”) waarbij die intensiteit geanticipeerd wordt (in de toekomst) of gereconstrueerd wordt (in het verleden). Omdat we kiezen om causaliteit als fundamenteler te beschouwen dan tijd, is het verleden hier te interpreteren als de aspecten die noodzakelijk zijn voor het “nu” en de toekomst is te interpreteren als de aspecten waarvoor het “nu” noodzakelijk is (de dualiteit met aspecten die voldoende zijn moet ondertussen al duidelijk zijn). De transformatie met de logaritme maakt van een exponent een lineaire parameter (met coëfficiënt evenredig met 1±k), volledig in overeenstemming met de manier waarop we een ongekende eenheid (processtap) willen meten die enkel toeneemt of enkel afneemt. Noteer dat de logaritme enkel gedefinieerd is voor positieve getallen.
Hieronder de basispatronen die ontstaan voor k=0,2 met vierkant symbool en k=0,3 met ruitsymbool en dertig stappen in intensiteit. In beide gevallen hebben de laagste intensiteiten de grootste verandering nodig van aantal processtappen. Noch de waarden voor de logm/log(1+k) als de waarden voor logm/log(1-k) zijn asymptotisch en we herkennen een positieve feedback in de twee gevallen. De curve kan voor grote intensiteiten goed benaderd worden als een lineaire benadering tussen twee parameters, wat goed overeenkomt met onze intuïtieve notie van de parameter “tijd”.
logm/log(1+k) |
Wordt groter vanaf 0 naar verdere + |
Positieve feedback in de positieve zin. Grotere intensiteit komt overeen met een tijdstip verder in de toekomst |
|
logm/log(1-k) |
Wordt kleiner vanaf 0 naar verder - |
Positieve feedback in de negatieve zin. Grotere intensiteit komt overeen met een tijdstip verder in het verleden |
|
We merken nu op dat, wanneer ook de intensiteiten tussen 0 en 1 geplot worden, de nul asymptotisch benaderd wordt en er dan een exponentieel veel groter verschil in processtappen overeenkomt met een kleine intensiteitswijziging. Welke klok we ook zouden gebruiken, in een ver verleden “liep ze trager”, wat betekent dat de resolutie toen niet gepast was om kleine intensiteitswijzigingen waar te nemen. Bijvoorbeeld: de verdubbeling van de intensiteit van een buffer had niet waargenomen kunnen worden omdat de klok dat niet kon genereren, ze genereerde bijvoorbeeld al onmiddellijk een ver-n-voudiging (met n een ongekend groot getal). Dit doet onmiddellijk denken aan wat er kon waargenomen worden “vlak na” het hypothetisch moment van de big bang.
Hieronder de patronen die ontstaan voor k=0,2 met vierkant symbool en k=0,3 met ruitsymbool en zeventig stappen in intensiteit met een intensiteitsverschil van 0,033. Voor de verschillende groottes van k treedt een inversie op bij het nulpunt van de waarden (de eenheid van de intensiteit).
logm/log(1+k) |
De waarden gaan van de tijd in een ver verleden (constructie van een mogelijk verleden) over een nulpunt in de tijd in de richting van toenemende tijd (constructie van een mogelijke toekomst). |
Positieve feedback in de positieve zin |
|
logm/log(1-k) |
De waarden gaan van de tijd in een verre toekomst (constructie van een mogelijke toekomst met een kleine intensiteit) over een nulpunt in de tijd in de richting van afnemende tijd (constructie van een mogelijk verleden met een grote intensiteit). |
Positieve feedback in de negatieve zin |
|
De lijn met ordinaat gelijk aan nul is het “nu” van het agens, de werkelijk die voor het agens dringend en belangrijk is. Het “nu” is het “ja” van de waarneming, en tevens het “neen” van een andere waarneming. Het is de 100% zekerheid: “dat spoor klasseer ik als het aspect dat aanwezig is (of het “anders aspect” dat afwezig is)”. Het “nu” heeft een resolutie, een bereik in het verleden en in de toekomst wat we kunnen modelleren als de breedte van een band rond de abscis as tussen ordinaat +ε en -ε met ε een willekeurig klein getal. Het verschil tussen de eenheid (1+k) en (1-k) is te merken in de intensiteiten die buiten de waarneming vallen in die band: het verleden voor (1+k) en de toekomst voor (1-k).
We kunnen nu de agentia met k=0,2 (vierkant) en k=0,3 (ruit) met elkaar vergelijken. Een bepaald intensiteitsverschil komt voor de kleinere k en dus kleinere onzekerheid overeen met een groter tijdsverschil. Het agens met een kleinere eigenwaarde zal daarbij een bepaalde intensiteit met een verder verleden verbinden maar ook met een verdere toekomst (voor de twee soorten feedback) vergeleken met een agens met een grotere eigenwaarde. Maar ook: een agens die een kleiner verschil in intensiteiten kan waarnemen (los van de eigenwaarde) zal een kleiner “nu” hebben. Als de waarneming een groter verschil nodig heeft dan zal het “nu” groter zijn vergeleken met het andere agens. Dit maakt de volgende interpretatie mogelijk: een kleiner verschil in intensiteit waarnemen kan doordat het agens de werkelijkheid met meer onderscheidingen kan opspannen. Maar dat betekent ook dat er minder zekerheid is over de waarneming. Wanneer we dat combineren met de eigenwaarde (een grotere k betekent dat er een grotere onzekerheid is in welke toestand het proces zich bevindt) kunnen we besluiten dat, voor dezelfde werkelijkheid, met evenveel onderscheidingen dus, het agens met de grotere eigenwaarde meer onzeker is zowel over verleden als toekomst dan het agens met kleinere eigenwaarde en daarenboven die toestand sneller bereikt. Het agens dat dan een kleinere onzekerheid heeft (kleinere k) zal voor een zelfde intensiteitsverschil pas later “gedwongen worden” om te reageren op het verder toenemen van de onzekerheid en zal pas later actie ondernemen (een waarneming uitvoeren en zo een collaps uitvoeren in de opgespannen werkelijkheid) dan het agens met een grotere eigenwaarde en dus grotere onzekerheid.
Door de inverse van de waarden te nemen is de singulariteit goed zichtbaar.
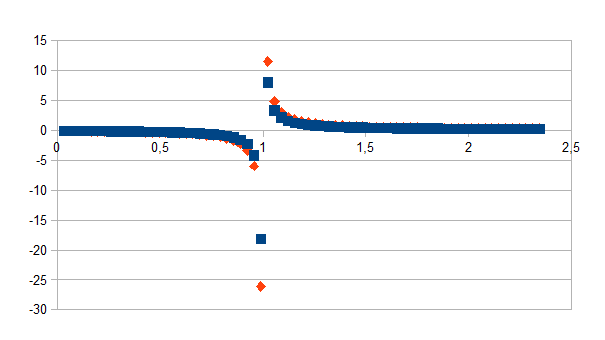
De
betekenis van de discontinuïteit op een onbegrensd grote
toekomst/verleden kan als volgt geïnterpreteerd worden. De
anticipatie naar positieve waarden van de tijd is een constructie. Er
zal in de toekomst ook altijd iets anders gebeuren dan datgene dat
kan geanticipeerd worden. De anticipatie naar negatieve waarden van
de tijd is eveneens een constructie, die gewoonlijk reconstructie
genoemd wordt omdat hier ook geldt dat niet alle aspecten van een
waarneming in het verleden kunnen ge(re)construeerd worden. Er zal in
het verleden ook altijd iets anders gebeurd zijn dan datgene dat kan
ge(re)construeerd worden. De anticipaties die verbonden zijn aan een
bepaalde waarnemingsresolutie (verschil dat een verschil maakt)
strekken zich zowel naar het verleden als naar de toekomst onbeperkt
uit. De enige singulariteit is het ervaren nu, de beslissing “ja”
te zeggen, de singulariteit van elke meting. Een potentiële
werkelijkheid heeft geen singulariteit, elke tralie kan immers
voorgesteld worden als een
hyperbol.