Interactie van twee soorten is te modelleren met bestaande soorten. De evolutie van bestaande soorten is te modelleren door het aantal (elkaar uitsluitende) individuen te tellen terwijl we het proces volgen met behulp van een monotoon toenemend spoor dat daar onafhankelijk van is (gewoonlijk het spoor van een klassieke klok). Tot nu toe hebben we enkel maar de interactie van twee soorten onderzocht, dit is een eerste maar wel belangrijke benadering omdat we enkel op die manier competitie kunnen modelleren. Een competitie is immers enkel helder te modelleren met maar twee soorten die zich gedragen als entiteiten die ofwel een symmetrische relatie hebben met elkaar, ofwel een asymmetrische. Er zijn dus twee buffers (entiteiten) waarvan de intensiteit gemodelleerd wordt, en de intensiteit is een aantal maal een eenheid, eenheid die voor elke buffer anders gemeten zou kunnen worden. Bij competitie tussen twee buffers is de toename of afname van intensiteit ofwel in de ene buffer, ofwel in de andere buffer gemeten: neemt de intensiteit in de ene toe, dan neemt de intensiteit in de andere af.

Daarenboven zijn we er in geslaagd om met maar twee buffers een monotone toename van intensiteiten te modelleren en dus iets dat zich als tijd gedraagt en dus ook als tijdmeting kan gebruikt worden. Dit zeer primitief model is niet anders dan de modellering van de synchronisatie tussen twee klokken. Dit is een begrip dat we kennen uit de relativiteitstheorie, maar in het model uit het haakformalisme moeten we niets veronderstellen over ruimte, de veronderstelling van toestanden is voldoende. De impliciete veronderstelling hierbij is dat we een onuitputtelijke bron hebben ofwel een niet te vullen put en we zullen die veronderstelling nu modelleren.

In wat volgt zullen we op het eerste model verder bouwen door het uit te breiden tot we m buffers kunnen modelleren die een gesloten netwerk vormen. We doen dat stap voor stap omdat er vanaf drie buffers meerdere relaties tussen die buffers mogelijk zijn. Dit betekent dat we minimaal dus drie buffers veronderstellen: minimaal dus twee bestaande en één die nieuw kan zijn wanneer die een causale relatie weergeeft met de twee andere en hierdoor een coördinatie tussen knooppunten veronderstelt: aspecten van het proces worden simultaan gerealiseerd. Competitie is dan niet meer relevant. Om dat te modelleren veronderstellen we dat één van de (minimaal) drie slechts als entiteit kan waargenomen worden als gevolg van de noodzakelijke aanwezigheid van twee andere in de juiste intensiteit. Dat is een gecoördineerd en een causaal verband: is de causaliteit in de ene richting noodzakelijk (p en q zijn noodzakelijk voor r) dan is de causaliteit in de andere richting onvermijdelijk (r is voldoende voor zowel p als q). Hierbij gaan we er ook van uit dat het aantal buffers en de causale koppeling ertussen niet verandert, enkel de intensiteit van de buffers. Om dat vast te stellen zouden we (1) dat kunnen verwachten, en dan zouden we “lang genoeg moeten wachten”, en misschien zullen we tevergeefs wachten, maar (2) we zouden het ook gewoon plots, op het onverwachts, kunnen vaststellen als we ervoor open genoeg zijn. Dat ook de koppeling niet verandert betekent impliciet dat we een (causale) ordening in minimaal drie buffers moeten vastleggen en dat kan dus niet anders dan dat we daar ook de intensiteiten bij betrekken. De zin van de ordening wordt gegeven door (minstens één relevante) bron en (minstens één relevante) put. We laten ons hierbij inspireren door de ervaringen met de modellering van chemische reactiesystemen en hun stelsel reactievergelijkingen met behulp van incidentie matrices die inwerken op vectoren van concentraties van reactiekernen. Hiermee kunnen we buffers modelleren die we kunnen verwachten en die slechts op een bepaalde processtap een intensiteit krijgen die verschilt van nul, terwijl ook de intensiteit van die buffers terug gelijk kan worden aan nul. De buffers modelleren we dus als een vectorruimte die opgespannen wordt door een aantal basisvectoren, de verwachte entiteiten in een causaal verband die enkel van intensiteit onbekend zijn. De precieze ordening herkennen we in de ordening van de vector en matrix elementen zoals we dat al gebruikt hebben in het geval van slechts twee knooppunten.

We veronderstellen dus minimaal drie processen van toename of afname van intensiteiten en dus minimaal drie buffers met intensiteiten op een bepaalde stap die met elkaar verbonden zijn door relaties van positieve of negatieve feedback. We noemen de drie buffers b₁, b₂, b₃. De intensiteiten zijn er, en zijn nu gemeten. We veronderstellen dat het proces dat de intensiteit van b₃ gegenereerd heeft (in het verleden bijvoorbeeld) enkel kan starten (en dan ooit eens een intensiteit groter dan nul bereikt heeft) als de processen die de intensiteit van b₁ en de intensiteit van b₂ gegeneerd hebben een intensiteit bereikt hebben die daarvoor noodzakelijk is. Hiermee modelleren we een causale koppeling (indien b₁ en b₂, dan b₃, deze “en” is een conjunctie). Dit betekent dat de laatst toegevoegde eenheid aan de intensiteit zal bepalen wanneer een soort van buffer b₃ gegenereerd wordt en b₃ dus een intensiteit krijgt verschillend van nul. Als reactievergelijking zouden we dan noteren dat b₁+b₂→b₃, maar dit is niet voldoende: de koppeling wordt ook beschreven door de getallen a₁, a₂, a₃. We kunnen ons dat voorstellen als: “het aantal a₁ bijkomende (Δ) entiteiten van soort b₁ vormen met het aantal a₂ bijkomende (Δ) entiteiten van soort b₂ het aantal a₃ bijkomende (Δ) entiteiten van soort b₃”. Dit modelleert de causale koppeling (de “indien…, dan…” constructie) tussen de processen en dus ook de ordening: de conjunctie van een bepaalde bijkomende intensiteit van het eerste proces met een bepaalde bijkomende intensiteit van het tweede proces is een noodzakelijke voorwaarde om het derde proces te starten. Als reactievergelijking zouden we dan noteren dat a₁b₁+a₂b₂=a₃b₃. Hier kunnen we het gelijkheidsteken gebruiken omdat we hiermee de stoichiometrie getrouw weergeven, bijvoorbeeld (n+m)O₂+pH₂+qH₂O=mO₂+(2n+p+q)H₂O, een reactievergelijking die aangeeft dat er in een omgeving met overvloedige aanwezigheid van H₂O niet genoeg H₂ aanwezig is om alle O₂ om te zetten tot H₂O. Het gelijkheidsteken is een korte notering voor een dynamisch evenwicht (er wordt zowel een → als een ← verondersteld).

De bijkomende entiteiten kunnen we meten door het verschil te nemen van de intensiteit van de buffers in twee opeenvolgende toestanden waarbij we een strikt geordende parameter n gebruiken. Bijvoorbeeld voor de intensiteit van de soort buffer₁: het getal a_1n - a_1n+1. Het verschil zorgt ervoor dat gelijk welk referentiepunt kan gekozen worden, we kunnen dus altijd meten zelfs al is er niets bekend over datgene “dat ervoor zou gekomen zijn” (we meten een Δ).

De meest eenvoudige situatie is dan dat er zich op een bepaalde processtap één entiteit bevindt in b₃ en dat het volgende moment dat iets waargenomen wordt in die buffer er zich twee entiteiten bevinden. Dat is een verdubbeling en dat is te tellen. De verandering is discontinu, de twee entiteiten sluiten elkaar uit, wat in het voorbeeld met stoichiometrie duidelijk werd. De verandering is causaal geordend: als we twee entiteiten b₃ waarnemen dan nemen we simultaan één entiteit b₃ waar. De noodzakelijke voorwaarden voor het proces zijn gekend, en ook de voldoende voorwaarden. Het zou natuurlijk kunnen dat we veel noodzakelijke voorwaarden over het hoofd zien. Maar wat we wel weten is dat, als de bijkomende intensiteit a₁ niet bereikt is, het proces niet doorgaat, en dit is gelijkaardig als voor de bijkomende intensiteit a₂ want al onze experimenten met kleinere intensiteiten hebben dat uitgewezen. Toch zou het best kunnen zijn dat er nog andere noodzakelijke voorwaarden zijn. We kunnen altijd meten zelfs al is er niets bekend over datgene “dat ervoor zou gekomen zijn”. Volledig gelijkaardig kunnen we dan afleiden dat als we een intensiteit a₃ meten van de buffer b₃ dat we dan minimaal zeker zijn van de intensiteiten a₁ en a₂.

Deze modellering is goed onderbouwd in het haakformalisme. Buffers zijn onvermijdelijk telbare entiteiten en dus atoomburen en om het gedrag van buffers te modelleren zijn dus de technieken van de lineaire operatoren geschikt. Lineaire operatoren met willekeurige reële waarden kunnen immers gebruikt worden om een kandidaat tralie te construeren tot op het niveau van de atoomburen. Die tralie kan de intensiteiten verklaren die waargenomen werden aan elkaar uitsluitende toestanden. We geraken hiermee juist op de diepte van de atoomburen als gemodelleerde entiteiten en de intensiteiten staan voor de “laatst toegevoegde onderscheiding” die impliciet in de matrix structuur verborgen zit. Willen we diepere relaties construeren dan kunnen we dat met tensoren (geneste splitsingen), maar dat is nu niet de focus. Een ander type matrix operatoren (die projectoren zijn) kan zelfs een niet op voorhand gekende structuur modelleren waarbij de metrische afstand tussen niveaus een rol speelt (de kwantum hypothese), die kan verwacht worden maar die enkel achteraf kan gekend worden (na “de meting”, na “de collaps”).

Een praktische klok

Een matrix A_ij modelleert als eenheid dus de causale koppeling van intensiteiten van de “interne knooppunten” van een netwerk, dat zijn de knooppunten die zowel voldoende als noodzakelijke voorwaarden zijn voor andere knooppunten uit het netwerk en daardoor een gesloten geheel vormen. De kwantiteiten in een m×m matrix A_ij modelleren de verdubbelingstijd van de m gekoppelde buffers (bijvoorbeeld metabolieten van een spontaan proces). Zelfs als we geen toegang hebben tot die buffers (en dus die klok geen praktische klok kan zijn), toch kunnen we met deze klok interageren door een mogelijke koppeling te zoeken met externe buffers. Wat we dan kunnen modelleren is de productie zelf van sporen en voor een betrouwbare klok mag de productie van sporen de interne dynamiek niet beïnvloeden.

Dat kan op twee manieren die de causale koppeling met de omgeving waarneembaar maken.

• Ten eerste kunnen we onderzoeken of we door intensiteiten van buffers te veranderen het proces kunnen stoppen. Die buffers moeten dus toegankelijk zijn voor ons en dat maakt ze “extern”, we noemen ze input knooppunten van het proces. Als die buffers niet een bepaalde intensiteit hebben gaat het proces niet door. Dit is een noodzakelijke voorwaarde (“indien niet…, dan niet...”).

• Ten tweede kunnen we onderzoeken of er toegankelijke buffers zijn waar we intensiteit kunnen van aftappen zonder dat het proces stopt. Dat maakt dat ook deze buffers “extern” zijn, we noemen ze output knooppunten van het proces. Het doorgaan van het proces is een voldoende voorwaarde voor het veranderen van de intensiteit van die buffers (“indien wel…, dan wel...”).

Meer dan dat hebben we niet nodig, hoe ingewikkeld ook de m gekoppelde buffers zouden kunnen zijn, of we ze nu gemodelleerd hebben of niet. Immers, een matrix A_ij zullen we altijd kunnen schrijven als een som van matrices met op sommige plaatsen -∞ voor de operatie “maximum” (en gelijkaardig +∞ voor de operatie “minimum”) en elke matrix uit de som kan een buffer modelleren.

Veronderstel nu zo’n m×m matrix waarvan alle cellen gelijk zijn aan ±∞ die inwerkt op een vector x met m componenten. Dan stopt het proces want de operatie van de m×m matrix op x is dan niet anders dan een x waarbij de m componenten gelijk zijn aan ±∞ en die dus buiten de waarnemingsresolutie vallen.

Veronderstel nu zo’n m×m matrix waarvan enkel (sommige) kwantiteiten op de hoofddiagonaal verschillend zijn van ±∞ (het teken is afhankelijk van de beslissing of we maximum of minimum modelleren, intensiteit van -∞ voor de operatie “maximum” en +∞ voor de operatie “minimum”) en die inwerkt op een vector x met m componenten. De resulterende vector zal enkel intensiteiten hebben die verschillen van ±∞ voor de componenten die overeenkomen met de beperkte intensiteiten op de hoofddiagonaal van de m×m matrix. Dit betekent dat zo’n matrix kan modelleren welke buffers noodzakelijke voorwaarden zijn voor het proces want enkel die knooppunten zullen een evolutie kunnen ondergaan bij de volgende stap. Noem deze m×m matrix B. B kan een som zijn van matrices. De maximale B heeft dan enkel op de hoofddiagonaal “verdubbelingstijden” die verschillen van ±∞. Dus de vector Bx is de vector die door de (“onbekende”) matrix A zal veranderd worden in de vector van de volgende stap. We noemen deze “toegankelijke” vector op stap n y_n, dus y_n=Bx_n.

Maar dat betekent ook dat een gelijkaardige m×m matrix (gelijkaardig omdat sommige componenten niet anders zijn dan ±∞) kan modelleren dat de evolutie te volgen is enkel door bepaalde buffers te volgen. De transformerende matrix beschouwen we dan als een som van twee matrices waarvan een van die matrices vectoren transformeert met een intensiteit die het proces niet beïnvloedt. We weten dat omdat we er in slagen om van die buffers sporen af te tappen zonder het proces te beïnvloeden, ze zijn dan geen noodzakelijke intensiteiten voor het proces. Die sporen “verlaten” dan het netwerk zonder impact te hebben op het verloop van het proces. Dat betekent dat we in staat zouden zijn om de evolutie voor te stellen als het maximum (dit is voor de verdubbelingstijden een som operatie) van een a priori onbekende vector x_n met een bekende vector z_n die ons de sporen levert (bekend omdat het die buffers zijn en geen andere). Noem deze m×m matrix C, de maximale C heeft dan enkel op de hoofddiagonaal verdubbelingstijden die verschillen van ±∞. Dus wordt de volgende stap in het proces gegeven door de som van de (“onbekende, interne”) Ax_n met Cz_n. Dit is dus niet anders dan x_n+1 en dus geldt het systeem van twee simultane vergelijkingen:

y_n = Bx_n

x_n+1 = Ax_n + Cz_n

Dit systeem drukt dus de twee manieren uit om te interageren met het netwerk: we kunnen de noodzakelijke voorwaarden voor het proces wegnemen om het proces te stoppen en als we dat niet doen, dan kunnen we sporen van het proces uit het proces “verwijderen” zonder dat dit impact heeft op het proces zelf dat spontaan doorgaat: het onderscheidingen universum is groter dan strikt noodzakelijk. Er zijn dus buffers die we als extern aan het proces kunnen beschouwen, de eerste (y_n) zijn de bronnen van het proces (“indien niet…, dan niet...”), de tweede (z_n) zijn de putten van het proces (“indien wel…, dan wel...”). Dualiteit herkennen we in gelijkwaardige interpretaties: “De knooppunten die enkel voldoende voorwaarden zijn voor knooppunten in het netwerk, modelleren putten in het netwerk. De knooppunten die enkel voldoende voorwaarden hebben in het netwerk, modelleren bronnen in het netwerk”. De resulterende vergelijkingen zijn exact dezelfde.

We kunnen hiervan een voorbeeld geven met slechts twee buffers, waarvan we er één gebruiken als bron en de andere als put. De totale relatie van simultaneïteit (voor drie 2×2 matrices A, B en C) wordt dus het systeem van twee vergelijkingen:

(y_1n, y_2n)^T=B(x_1n, x_2n)^T want enkel die componenten van de x vector zijn actief bij een volgende stap, in dit geval dus een van de twee.

(x_1(n+1), x_2(n+1))^T=A(x_1n, x_2n)^T + C(z_1n, z_2n)^T want sommige componenten van de z vector hebben geen invloed op het proces, in dit geval dus ook een van de twee.

We geven hiervan een voorbeeld met getallen: we veronderstellen terug dezelfde 2×2 matrix A als (1, 8; 2, 3) die inwerkt op een vector x, genoteerd als kolomvector waarbij we de evolutie starten bij x(0)=(1, 0)^T. We construeren nu de matrices B en C met enkel relevante waarden op de hoofddiagonaal: B met een hoofddiagonaal als (-∞, -∞, -∞, 20) en C met een hoofddiagonaal als (100, -∞, -∞, -∞). We kiezen de getallen zodanig dat we beide intensiteiten in de grafiek heel duidelijk kunnen onderscheiden.

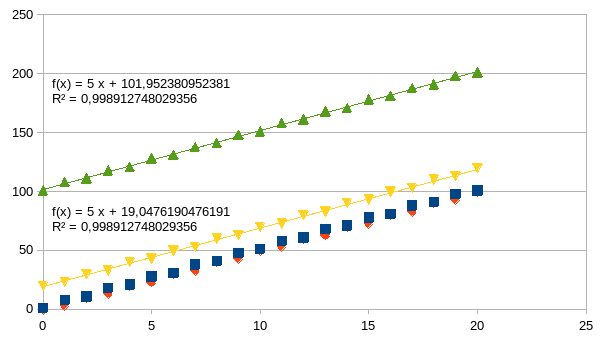
De intensiteiten van de bron buffer B (driehoek op de kop) en de put buffer C (driehoek op de basis) hebben exact hetzelfde verloop als de intensiteiten van de (ontoegankelijke) interne knooppunten (vierkant en ruit), het enige verschil is de waarde van de intensiteit (het startpunt, het snijpunt met de ordinaat).

Dit illustreert duidelijk wat we nu bereikt hebben in het model: een verschaling van de waarden die we veronderstelden in de oorspronkelijke klok. Het is een verschaling want we moeten beseffen dat deze intensiteiten exponenten zijn.

We veronderstelden een 2×2 matrix A gelijk aan (1, 8; 2, 3), die inwerkt op een vector x, genoteerd als kolomvector waarbij we de evolutie starten bij x(0)=(1, 0)^T. Dus bij het begin (stap 0) is het verschil van beide intensiteiten van de buffers gelijk aan 1. We hebben berekend dat bij de volgende stap het verschil 5 is en bij de stap daarna is het weer 1. In de tabel vergelijken we

Het is duidelijk dat het verschil (namelijk 80) waarmee gestart werd in het geval van input en output in de loop van de stappen behouden wordt. Dit is verantwoordelijk voor het behoud van de richtingscoëfficiënt. Het verschil dat aanleiding geeft tot de getallen in de laatste kolom kan willekeurig gekozen worden zolang het groter is dan het verschil in de voorlaatste kolom. Dit is dus niet anders dan een tijdrek (tijd dilatatie γ) want het enige verschil tussen beide netwerken is de intensiteit van de buffers op stap t. Inderdaad men stelt t=γt’ voor de veronderstelling dat x’=0. We zien dat t verschaald wordt met factor (1-v_rel²)^-1/2 dus t is altijd groter dan t’. Dat is de essentie van relativiteit want v_rel kunnen we interpreteren als gelijk welke v_ij. Aangezien de intensiteiten in de exponent voorkomen van onbekende eenheden verschillend van 1, zijn deze verschillen “verschillen van schaal”.

De “eigenwaarde posities” (de cellen van matrix A) die de relatie karakteriseren zijn dezelfde. Per stap meten we gewoon een groter getal, de veelvuldigheid per stap (de densiteit) is groter maar het verschil per stap is hetzelfde.

Dit geeft de mogelijkheid om de variatie in de sporen te beschrijven omdat we nu meer sporen hebben die het proces niet beïnvloeden, het heeft zin om te spreken over de toename of afname van sporen in de loop van het proces zonder dat het proces veranderd wordt. Het zijn deze aantallen die ons in staat stellen om van een snelheid van toename of afname te spreken per stap in de vorm van (n_i-n_i+1)/(n_i+n_i+1). Voor elke stap wordt de noemer groter (dat hebben we op de grafiek geïllustreerd), maar de teller varieert. We krijgen dus “meer ruimte” die we enkel kunnen beschrijven met meer onderscheidingen. Maar om dat te doen hebben we dus een nieuwe klok nodig want de klok die door matrix A beschreven wordt kan die stappen niet onderscheiden. We hebben een klok nodig die meer (elkaar uitsluitende) toestanden kan onderscheiden.

Gevolgen: de relativiteit van de steeds toenemende parameter

Een onmiddellijk gevolg van het herkennen van buffers waarvan de intensiteit het proces niet beïnvloedt is dus dat er gerust variatie kan zitten in de intensiteit van bron en put die niet gemodelleerd kan worden met de gekozen klok. Ondanks die (externe) variatie zal het spontaan (intern) proces niet stoppen. Dit kan modelleren dat een klok altijd met minder onderscheidingen kan gemodelleerd worden dan de onderscheidingen die nodig zijn om die variatie te beschrijven. De variatie maakt de werking van de interne klok niet onmogelijk en dit merken we zolang we voldoende input hebben en niet teveel output wegnemen. Binnen de waarnemingsresolutie (die ons de mogelijkheid gaf om bron en put te onderscheiden) zijn bron en put onafhankelijk van de interne buffers die de klok vormen. We kunnen ons dat voorstellen door te interpreteren dat de onderscheidingen die noodzakelijk zijn om de variatie te verklaren in bron en put niet noodzakelijk zijn voor de interne klok maar zouden kunnen gemodelleerd worden door een tweede klok. Die tweede klok zal, om ook weer een praktische klok te zijn die niet alle variatie moet kunnen beschrijven, slechts de repetitiviteit van een beperkt aantal onderscheidingen modelleren.

Elk proces dat een interne dynamiek volgt die causaal verklaard kan worden als een gesloten netwerk, kan als klok gebruikt worden die gevoed wordt door een bron die een noodzakelijke voorwaarde blijkt te zijn voor de klok, en die een put voedt waarvoor de klok een noodzakelijke voorwaarde blijkt te zijn. En duaal kunnen we zeggen dat elke klok een voldoende voorwaarde is voor het onderscheiden van een bron en het onderscheiden van een put.

De input en output die de interne klok niet beïnvloeden kunnen gebruikt worden om een interactie aan te gaan met andere klokken en juist die intensiteit van sporen hebben we gemodelleerd met de grootte van de populatie van bestaande soorten. De interne klok van de soort emitteert repetitief een nieuw individu en hoe meer individuen hoe meer er coördinatie kan ontstaan van hun gedrag en niet alle aspecten van individueel gedrag moeten beschreven kunnen worden om coördinatie te beschrijven.

Om variatie te verklaren moeten we minstens één causale ordening aannemen en dus een klok. De variatie die deze klok toelaat is “onzichtbaar” voor de klok (zoals een bepaalde idempotente eenheid “onzichtbaar” is voor een bepaalde operatie) en is enkel te modelleren ten opzichte van de strikte ordening van een andere klok. We ontsnappen niet aan de relativiteit van processtappen en dus van tijd. Maar dat betekent ook dat we enkel kunnen modelleren wat we met een klok kunnen anticiperen, want er zullen altijd processen zijn die niet gemodelleerd kunnen worden omdat er ook altijd iets anders gebeurt dan wat we doen gebeuren. Dat is het enige axioma en betekent dat er altijd iets zal gebeuren dat niet te anticiperen is en dat dus niet gerelateerd is aan de beperkte modellering van een praktische klok.

Klokken zijn gesloten netwerken die een spoor (“iets”) kunnen achterlaten zonder hun dynamiek te verliezen. Het zijn die sporen die we gebruiken om evoluties te modelleren. Niet alle sporen zijn relevant voor interactie en sommige buffers genereren dus sporen die verwijderd kunnen worden zonder de dynamiek in het gedrang te brengen. Een voorbeeld hiervan is de lucht die we uitademen, of andere excreties. Een tegenvoorbeeld is de emissie van nakomelingen, zonder deze emissie sterft de populatie uit. Interactie van entiteiten en de evolutie van hun populaties hebben we gemodelleerd als een proces waarbij “dat iets”, aangeleverd door een bron, getransformeerd wordt en geleverd wordt aan een put. De enige eis die we stelden is dat een kwantum van dat iets zich niet simultaan in meerdere buffers kan bevinden. Het “iets” moet dus een entiteit zijn die andere entiteiten uitsluit. Dat is typisch voor materie en niet voor informatie. Materie is “het Maxwell duiveltje” dat voor orde zorgt, materie is een informatiedrager.

In elke buffer kan dit “iets” op een andere manier gemeten worden en we kunnen de toename en afname van dit “iets” voor elke buffer volgen doordat we een ordening kunnen vinden die eigen is aan het proces en een monotone transformatie weergeeft van dit “iets” tussen bron en put, gemeten dank zij een proces verschillend van het gemodelleerde proces (de “externe klok”). Om het monotoon pad te beschrijven gebruiken we het begrip “evenwicht” en we zeggen dat elk proces de evolutie beschrijft van iets “ver van evenwicht” naar naar iets “in evenwicht”. Er is geen verandering waarneembaar zowel in de toestand “ver van evenwicht” (de toestand van de bron) als in de toestand “in evenwicht” (de toestand van de put), beide begrippen zijn enkel ten opzichte van elkaar gedefinieerd. Dit herkennen we als karakteristiek voor elk onderscheid: “iets” ten opzichte van “iets anders”.

Dit zijn zeer universele veronderstellingen en we herkennen dat we hiermee alle processen kunnen modelleren die karakteristieken hebben die ook wij hebben als agens-in-context. De communicatie die nodig is voor coördinatie van processen gebeurt met sporen die kunnen afgescheiden worden zonder het proces van de individuele klok te beïnvloeden, we beïnvloeden wel de klok van het gecoördineerde proces, maar dat is gewoonlijk de bedoeling: we willen beïnvloeden wat er simultaan kan gebeuren. We herkennen dit als het patroon van de co-evolutie van entiteiten die sporen achterlaten. Het “iets” interpreteren we in de huidige stand van wetenschap als “energie”, energie is iets materieels, iets dat getransformeerd kan worden in andere vormen, in andere buffers. We stellen dan vast dat we meer en meer in staat zijn energie materieel te bufferen in nieuwe entiteiten (soorten of eenheden die een intensiteit kunnen hebben) met een zekere permanentie zodanig dat we die energie niet verliezen. Dat zijn de soorten die kunnen blijven interageren met elkaar om bijvoorbeeld meer synergie te vertonen.

De klokken kunnen gesynchroniseerd worden, wat betekent dat er een relatie gevonden wordt tussen de processtappen van de ene en de processtappen van de andere klok. Tijdrek levert ons de sporen waarmee we nieuwe processen kunnen maken die doorgaan in buffers die causaal gekoppeld zijn en die dus nieuwe klokken zijn. We kunnen een hiërarchie onderscheiden in praktische klokken.

Een holon als klok

We hebben het dynamisch aspect gemodelleerd van de aanwezigheid van twee populaties die elkaar beïnvloeden. We onderscheiden een symmetrische en asymmetrische beïnvloeding. Het fundamenteel verschillend resultaat is te zien in de evolutie van beide soorten processen: slechts bij een symmetrische beïnvloeding kan een soort volledig verdwijnen zonder impact op het geheel, een asymmetrische beïnvloeding heeft altijd impact. We hebben nu ook de interactie onderzocht met nieuwe soorten die alleen maar kunnen ontstaan als de intensiteit van noodzakelijke soorten een nieuwe coördinatie mogelijk maakt en dus een nieuwe entiteit. Dit is fundamenteel om de activiteiten van ontwerpers te kunnen begrijpen en waarderen, want het is dat wat ze doen als ze nieuwe processen ontwerpen: andere en meer gewenste resultaten simultaan laten gebeuren.

Dit inzicht vinden we terug bij de concepten van symbiotische soorten en de hypothese dat ze een nieuwe entiteit (een nieuwe soort, “de symbiose”) vormen, gekarakteriseerd door een blijvende dynamiek en een nieuwe klok. Deze entiteit noemen we sinds de publicaties van Arthur Koestler een holon. Met verschillende holonen kunnen we een holarchie onderscheiden. Een holon is een entiteit waarin een onderlinge beïnvloeding van deelentiteiten waarneembaar is, zodanig dat ze van elkaar afhankelijk zijn. Een wereld waarin “iedereen van iedereen profiteert” blijkt voor iedereen de meest geschikte te zijn. Hierbij kan geen enkele deelentiteit uit de interactie verdwijnen, hoe groot of hoe klein de intensiteit van hun soort wel zou zijn. Intensiteiten van soorten worden dan op een dynamische manier binnen grenzen gehouden en de meerdimensionale attractor kan de holon karakteriseren. Elke holon kunnen we dan beschouwen als een eigen klok. We hebben dit onderzoek gevoerd met de hypothese dat we alle interagerende soorten en hun interacties en eigenwaarden kennen en dat nieuwe soorten ontstaan als gevolg van nieuwe interacties. Nieuwe soorten zouden bestaande soorten kunnen vervangen terwijl de “soort dynamiek” (de holon) niet verandert. Dit zouden we kunnen reconstrueren vanuit onderzoek, met behulp van fossielen, hoe soorten soorten in het verleden konden vervangen worden zonder de holon zelf te vernietigen. De nieuwe modellering kan misschien zorgen voor nieuwe inzichten hierin die door ontwerpers kunnen toegepast worden bij creëren van nieuwe producten, processen en systemen die andere producten, processen en systemen kunnen vervangen en die de holon “levende aardbol” niet vernietigen.