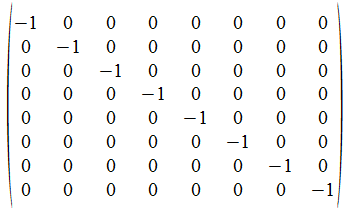Bij de ontwikkeling van verschillende morfisme voor het haakformalisme hebben we regelmatig matrix-operatoren kunnen vinden die inwerken op een geordende lijst structuren. Deze structuren kunnen de getallen +1, -1, 0 zijn die modulo 3 kunnen geïnterpreteerd worden, kunnen complexe of perplexe getallen (+1+i, -1-j enz...) zijn die eveneens modulo 3 kunnen geïnterpreteerd worden, maar kunnen dus ook algemene complexe structuren zijn die, juist dank zij de operator met elkaar kunnen gecombineerd worden op een lineaire manier.

De meest eenvoudige operatoren hebben we atomaire projectoren genoemd. Hiermee is er een één-op-één afbeelding mogelijk van een diagonaalmatrix met een som van ervaren atomen, atomen die dus niet simultaan kunnen ervaren worden, en die bij elk ervaren met een bepaalde intensiteit kunnen gewaardeerd worden als het waargenomen (gemeten) getal van een entiteit in een bepaalde momentane context. Die entiteit is dan de (stabiele, niet veranderende) entiteit die als een ervaren haakuitdrukking op atoom-buur niveau kan voorgesteld worden als <x_i><<x>_i> en die operationeel opgebouwd wordt uit een aantal m onderscheidingen die allemaal dezelfde ervaringswaarde hebben. Van moment tot moment verandert dan het relevante onderscheidingen universum. Dit kan gemodelleerd worden doordat de intensiteit m als coëfficiënt (momentane disjunctie, momentane invariant) bij de hele tralie (en dus ook de atomen) kan functioneren. Die intensiteit is een getal dat voldoet aan het axioma van het getal in het haakformalisme. Dit betekent dat er op de diagonaal dan ook andere reële getallen (niet enkel +1 ofwel -1) genoteerd worden en die modelleren dat op verschillende momenten verschillende onderscheidingen universa waargenomen worden waarbij iets telbaar stabiel blijft.

Met een voorbeeld: de diagonaalmatrix 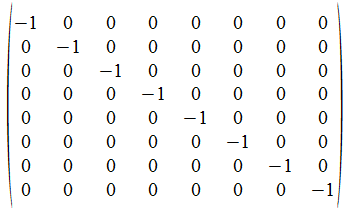vervangen we door een algemene diagonaalmatrix A, of [a_ij], waarin de a_ij dus reële getallen zijn.

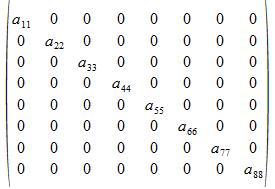
We herkennen deze matrix als een eigenwaarden matrix en kunnen we dus eveneens voorstellen als een som van n matrices van de soort n*n.

De vraag die zich nu stelt is of er een combinatie van coëfficiënten mogelijk is voor basisvectoren van één tralie die de coëfficiënten van de gemeten atoomvectoren oplevert en omgekeerd. Op die manier zouden we een zicht kunnen krijgen op de onderliggende basisvectoren die voor de entiteit allemaal dezelfde ervaringswaarde hebben. Een gerelateerde vraag is dan ook: stel dat men een operator heeft met enkel reële coëfficiënten (die inwerkt op een vector met enkel reële coëfficiënten) zijn op basis daarvan basisvectoren met coëfficiënten en ervaren atomen met intensiteiten af te leiden, met andere woorden zijn basisvectoren en atomen van een universum te construeren met behulp van alleen maar de informatie die in de operator gecodeerd is?

Deze vragen worden door de lineaire algebra bestudeerd en de disjunctie van intensiteiten met structuren maakt het mogelijk om een relatie te leggen van de taal die ontwikkeld werd in de lineaire algebra met de inzichten van het haakformalisme. We krijgen daarmee arrays (vectoren) van getallen als studieobject.

We beschouwen een willekeurige operator A met n kolommen en m rijen met n≥m, inwerkend op een willekeurige vector x voorsteld door de array (x₁, x₂, ...x_n)^T. Het resultaat is een kolomvector b.

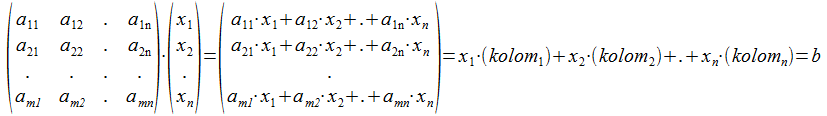
We schrijven Ax=b.

De kolomvector b met m componenten is een lineaire combinatie van de kolommen van de operator A, kolommen die vastliggen en gekoppeld aan de ordening van n. Dat betekent dat, ondanks de vrije keuze van de componenten van de kolomvector x, niet elke denkbare b met m componenten kan gemaakt worden. We noemen de verzameling vectoren b die kunnen gemaakt worden de kolomruimte van A. De kolomruimte van A is de verzameling vectoren met m componenten die gevormd kan worden door de kolomvectoren van A met elkaar te combineren. De dimensie van deze kolomruimte (het maximum aantal onafhankelijke vectoren) is r.

Sommige van die vectoren zullen niet te onderscheiden zijn van de nulvector met m-r componenten.

Volledig analoog kunnen we spreken van de rijruimte van A als de verzameling vectoren die gevormd kan worden door de rijvectoren van A met elkaar te combineren. Dit is ook in kolomformaat te schrijven door A te vervangen door zijn transpose A^T, waarbij (rij_i) gelijk is aan (kolom_i)^T voor i = 1 tot m.

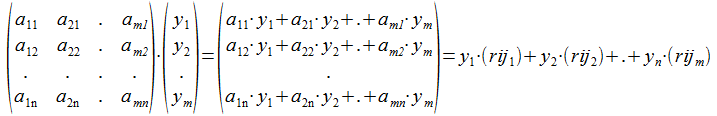
Sommige van die vectoren zullen niet te onderscheiden zijn van de nulvector met n-r componenten, wanneer de dimensie van de rijruimte en dus ook kolomruimte ((het maximum aantal onafhankelijke vectoren) r is.

Lineaire operatoren met willekeurige reële waarden kunnen dus gebruikt worden om een kandidaat tralie te construeren die de intensiteiten kan verklaren die waargenomen werden aan elkaar uitsluitende toestanden. Hiertoe hebben we niet meer nodig dan de vooronderstellingen van het gebruik van matrices en een inzicht in het 1-splitsing universum. We geraken hiermee echter niet dieper dan de atoomburen als gemodelleerde entiteiten.