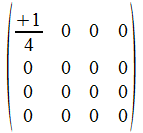In het algemeen zal het uitwendig product van gecollapste haakvectoren resulteren in symmetrische operatoren met een 0 op volledige lijnen en volledige kolommen. Atomaire basisvectoren nemen hierin een speciale plaats. Ervaren of gebeurde atomen resulteren in een operator met cellen die de getalwaarde 0 hebben, behalve één cel op de diagonaal.

Bijvoorbeeld: (x x x -) wordt vertaald naar (-1-i, 0, 0, 0)^T, die resulteert in de operator 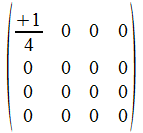waarin we onmiddellijk de normalisatie factor voor het twee-onderscheidingen universum verwerkten.

De inbedding van deze atomaire basisvector resulteert duidelijk eveneens in dezelfde operator, zodanig dat dit ook een afbeelding is voor (x x x .). Dus het gebruik van operatoren maakt de keuze voor een van de atomaire basisvector sets overbodig maar daarenboven is hier geen verschil meer tussen een “ervaren en gebeurde operator” voor een vector en zijn inbedding: wat in het potentiële geval geldt voor alle vectoren, geldt in het geval van vectoren met een waarde enkel voor de atomaire vectoren.

Deze atomaire operatoren zullen één component van een vector selecteren, bijvoorbeeld in de grondvorm:

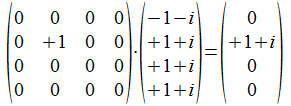
We kunnen dus het volgende noteren voor elke welgevormde haakuitdrukking in zijn afbeelding in het 1-splitsing universum: |x> =Σ|e_i><e_i|x> met de som over al de atomaire basisvectoren |e_i> (voor een n onderscheidingen universum zijn dat er 2ⁿ).

Noteer: een matrix heeft twee diagonalen. Een +1 op de andere diagonaal kan enkel bekomen worden als men in de bitstring van de elkaar toegevoegde vectoren een van deze vectoren verandert door zijn contraduale vector (en dus de volgorde van de bits omkeert).

Dit maakt ook duidelijk dat niet elke matrix met +1 en 0 een modellering is van een punt in het haakformalisme.