Als gevolg van stelling4 hebben we de volgende definitie gegeven van (ir)relevantie: wanneer de waarde van een punt niet moet gekend zijn om een waarde aan een ander punt toe te kennen zullen we zeggen dat (de waarde van) het eerste punt irrelevant is voor (de waarde van) het tweede punt. Irrelevantie is “een verschil dat geen verschil maakt”. Relevantie is “een verschil dat een verschil maakt”.

De modulo3 voorstelling maakt het mogelijk een collaps uniek te coderen. Bijvoorbeeld: de keuze om de waarde <> aan a te geven (en dus de waarde <<>> aan <a>) wordt in een twee onderscheidingen universum gecodeerd door (x-x-). De resulterende relevante tralie heeft dan nog maar vier punten: (x+x+), (x-x+), (x+x-), (x-x-).

We merken nu op dat er geen verschil is tussen een punt met codering (xxxxxx+--) en een met codering (x+--), behalve het universum waarin ze uitgedrukt zijn. De irrelevante bits zijn met een x aangeduid en de relevante bits met ofwel + ofwel -. De relatie die hiermee geïntroduceerd wordt noemen we de relatie van (ir)relevantie en kunnen we nu in zijn algemeenheid onderzoeken.

We onderscheiden twee waarden: “.” en “x”. Het typografisch punt staat voor een betekende waarde die verder niet gekend moet zijn, “x” staat voor een don't care. Dit zijn de enige waarden die een modulo3 bitpositie kan innemen: ofwel is de bitpositie don't care, ofwel heeft de bitpositie een betekende waarde (die ofwel – ofwel + is, in binair formaat is dit 0 ofwel 1).

De nieuwe waarden “.” en “x” zullen we elkaars orthogonale involutie noemen: de orthogonale involutie van “.” is “x”, de orthogonale involutie van “x” is “.”. Een orthogonale involutie zullen we ook als orthogonalisering benoemen. Bijvoorbeeld: de orthogonalisering van (xx..xxx.) is (..xx...x).

De relatie van (ir)relevantie heeft twee fundamenteel verschillende richtingen die we aangeven met de operaties + versus ×. Merk op dat + hier een operatie voorstelt en niet een waarde. Merk op dat × ook een operatie voorstelt en niet een waarde. Aangezien de waarden die gehanteerd worden met de relatie van (ir)relevantie “.“ en “x” zijn kan hierbij geen verwarring optreden.

De relatie wordt in de volgende tabel vastgelegd.

Merk op dat we de twee richtingen aangeven voor de éne relatie. Is er minstens één bit relevant dan is a+b relevant, is er minstens één bit niet relevant dan is a×b niet relevant en: a+b is niet relevant slechts als beide bits niet relevant zijn, a×b is relevant slechts als beide bits relevant zijn.

De tabel is het gemakkelijkst te memoriseren door de klassieke som- en product-regels te volgen voor “x” als getalnul en “.” als een willekeurig, niet nader gespecificeerd positief getal (dit is bijvoorbeeld te bereiken door voor elke bit zijn kwadraat te nemen).

We kunnen nu de volgende tabel construeren die volledig analoog is met de tabel van de 16 mogelijke binaire waarden van twee onderscheidingen. De haken zijn nu vervangen door rechte haken, waarmee we orthogonaliteit coderen ([] is de orthogonalisering van [[]], dus bijvoorbeeld: a is orthogonaal met [a]), de nevenschikking is vervangen door ×, het samenspel van × en [] genereert +. We geven in de tabel in de eerste en laatste kolom de vertaling van de bitstrings in functie van zowel × als +.

De dualiteit voor onderscheidingen is in deze tabel gecodeerd zoals bij gewone haken, bijvoorbeeld [a]×b is het duaal van [a+[b]]. Het is hierdoor ook mogelijk om vormen te maken waarin de beide operaties, + en ×, voorkomen. We zullen dit echter vermijden en bij voorkeur enkel met × werken.

Deze tabel kan als volgt bestudeerd worden: wat in a×b relevant is, is ook in a relevant. Wat in a relevant is, is ook in [[a]×[b]] relevant. Omgekeerd: wat in [[a]×[b]] irrelevant is, is ook in a irrelevant, is ook in a×b irrelevant. Dit maakt duidelijk dat de relatie van relevantie een partiële orderelatie is met p+q (of [[p]×[q]]) en p×q (of [[p]+[q]]) als extrema van de relatie.

Naar analogie met wat we introduceerden bij de relatie van simultaneïteit kunnen we nu ook een symbool introduceren voor de relatie van relevantie. We gebruiken hiervoor ≥ versus ≤ met de index r voor relevantie. De keuze van het “groter dan of gelijk aan” symbool en het “kleiner dan of gelijk aan” symbool is gemotiveerd doordat de relatie van relevantie een partiële orderelatie is. Inderdaad, we kunnen ook hier de verschillende ordeningen in een tralie weergeven die ofwel monotoon minder relevant, ofwel monotoon meer relevant zijn. Elk monotoon pad van punten die doorlopen worden heeft maar één punt op elk niveau van de tralie (we kiezen om het supremum van p en q als p+q te nemen, het infimum als p×q):

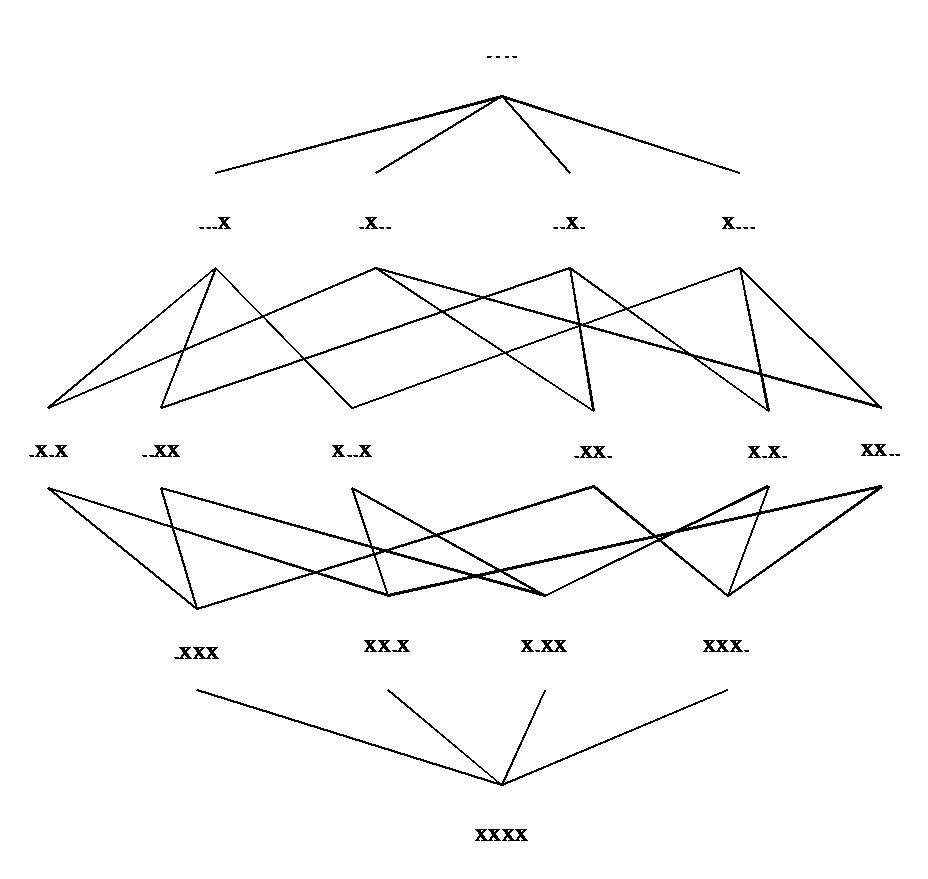
Het patroon van de tralie is ondertussen goed gekend en geeft nu de relatie van relevantie weer tussen gecollapste punten, waarbij het supremum van de hele tralie in de relatie van relevantie een willekeurig potentieel punt is, en het infimum in de relatie van relevantie de al-nul vector.

Elk van de punten die in de tralie gecodeerd worden heeft een complexe relatie met verschillende punten van een potentiële tralie. Het is niet omdat we hier de symbolen a en b gebruiken, dat a en b onderscheidingen zijn, a en b zijn immers gecollapste tralies, elk codeert voor meerdere gecollapste punten, die echter dezelfde collaps delen.

Bijvoorbeeld: neem voor a de codering (.x.x). Dit is een patroon van de volgende mogelijk vier gecollapste punten: (+x+x);(+x-x);(-x+x);(-x-x). Voor de relatie van simultaneïteit is (+x+x) het supremum van deze vier en (-x-x) het infimum van deze vier. Dat betekent dus ook, als we voor b de codering (..xx) nemen, dat a×b staat voor de twee gecollapste punten (+xxx) als supremum van simultaneïteit en (-xxx) als infimum van simultaneïteit.

We zeggen p is relevanter dan q, met symbool p≥_rq, wanneer [p]×q niet kan onderscheiden worden van de al-nul vector.

We zeggen p is minder relevant dan q, met symbool p≤_rq, wanneer p×[q] niet kan onderscheiden worden van de al-nul vector.