Interactie van entiteiten kunnen we ook interpreteren als een interactie van soorten. Een soort is een onderscheiding waarop individuen zich niet onderscheiden en is dus even abstract als het begrip “entiteit”. Soorten kunnen dus ook in competitie staan ten opzichte van elkaar, of kunnen ook elkaar aanvullen. Historisch gezien zijn “soorten” op de eerste plaats onderscheiden en bestudeerd in de biologie of in de ecologie (en pas veel later als fermionen en bosonen in de kwantummechanica). De intensiteit van een soort wordt dan een populatie genoemd. We zullen de interactie van soorten daarom gemakkelijk kunnen illustreren met voorbeelden uit die domeinen, maar voor het inzicht is dit geen beperking. Het onderzoek is trouwens gemotiveerd door cybernetische bezorgdheden: hoe kunnen we autonome entiteiten ontwerpen die in een constructieve interactie staan met bestaande autonome entiteiten (die eventueel niet ontworpen werden), die ze respecteren en zo kunnen co-evolueren.

Enkele voorbeelden van soorten die niet ontworpen werden: cellen in een lichaam worden door eenzelfde bron gevoed of moeten dezelfde route gebruiken om afval weg te krijgen en staan dus hiervoor in competitie. Maar cellen kunnen elkaar ook perfect ondersteunen. Twee individuele bomen staan in competitie met elkaar om allerhande voeding (licht, lucht, water enz…) maar staan ook in competitie met bijvoorbeeld gras. We merken dat in sommige milieus bomen die elkaar ondersteunen het beter doen dan gras, zodanig dat er in sommige milieus zelfs geen gras meer voorkomt. Er is dus ook competitie tussen soorten, vergelijkbaar met de competitie tussen individuen binnen één en dezelfde soort, maar zoals het voorbeeld van de verschillende soorten cellen in een lichaam (of verschillende soorten in een bos) illustreert, is de interactie tussen soorten veel complexer dan enkel competitie (zoals ook de interactie tussen individuen veel complexer is dan enkel competitie).

De competitie tussen individuen is merkbaar wanneer we de intensiteit van een aspect van de individuen kunnen tellen. De interactie tussen soorten is merkbaar wanneer we het aantal individuen binnen een soort kunnen tellen, niet de intensiteit van “iets” op individueel niveau (zoals bijvoorbeeld de biomassa van een individu). Biotische soorten zijn in staat minstens één individu van dezelfde soort te genereren (dat is een van hun emissies). “Nul” en “één” zijn dus goed gedefinieerd en ook het ander extremum is meetbaar: dit wordt in de biologie een “draagkracht” genoemd (en in de techniek de maximale capaciteit van een buffer). Een bepaald milieu heeft een maximale draagkracht voor een bepaalde soort, en dat geldt zelfs als er geen andere soorten aanwezig zijn. Daarmee bedoelt men de maximale populatie (meervoudigheid van individuen) die voor langere tijd in een bepaalde leefomgeving habitat vindt, voedsel, enz ... en aan meerdere andere levensbehoeften kan voldoen. In die levensbehoeften onderscheidt men abiotische factoren en biotische factoren. Biologische soorten zijn ook biotische factoren in een bepaald milieu; ze kunnen zich spontaan reproduceren en verdwijnen soms ook. Zo is het zinvol om te spreken van een groeisnelheid van de soort (groei kan positief of negatief zijn) als de toename of afname van het aantal individuen. Dit is afhankelijk van het milieu: er is een minimale populatie nodig en er kan slechts een maximale populatie in stand gehouden worden. Een biotische factor heeft dus een specifieke groeisnelheid (een eigenwaarde die leidt tot verdubbeling of halvering van de intensiteit) en de groeisnelheid zal van milieu tot milieu verschillen en de entiteit die de intensiteit kan hebben heeft noodzakelijkerwijze méér dan één individu. De competitie, rivaliteit, samenwerking, tegenwerking, in het algemeen interactie tussen soorten in één en hetzelfde milieu kan dus minimaal gemodelleerd worden door de intensiteit van twee biotische factoren en hun groeisnelheid met elkaar te koppelen, twee biologische aspecten die elk a priori een andere intrinsieke groeisnelheid en minimale en maximale capaciteit hebben. Hierbij zullen we expliciet ons onderzoek voeren in de richting van de relaties met soorten die we wel kunnen ontwerpen.

Het modelleren van dit gedrag werd voor het eerst geprobeerd door Lotka en Volterra in het begin van de 20ste eeuw met behulp van het logistisch differentie model dat voor populatie onderzoek een eeuw vroeger reeds gesuggereerd werd door Pierre-François Verhulst. We zullen dit model inzetten in dat wat volgt, maar onze interpretatie is nieuw dank zij het fundamenteel begrijpen van de causale relaties.

We zullen twee soorten interactie onderscheiden: een symmetrische en een asymmetrisch. Bij de symmetrische relatie spelen twee entiteiten of twee soorten dezelfde rol, bij de asymmetrische relatie is dat niet het geval. Dit is een belangrijk onderscheid omdat het de entiteit (“biotische factor”, “soort”, ...) bepaalt.

Bij de symmetrische relatie behoren twee entiteiten (of soorten) tot dezelfde (meer abstracte) soort. De soort wordt bepaald door de aspecten waarop de entiteiten (of soorten) zich niet onderscheiden van elkaar. Dit zijn evidente aspecten aangezien we altijd soorten kunnen vinden die eenzelfde milieu delen en zich op dit punt niet onderscheiden van elkaar. Ze “delen” dan misschien ook een onderscheidingen universum, een medium waarin ze communiceren door gematerialiseerde sporen achter te laten die functioneren als symbolen. Hun universum wordt dan door dezelfde onderscheidingen opgebouwd, dit zijn onderscheidingen die in het universum van de ene soort dezelfde waarde hebben als in het universum van de andere soort.

Bij de asymmetrische relatie behoren twee entiteiten tot een verschillende soort hoewel ze hetzelfde universum kunnen delen. De soort wordt bepaald door minstens één aspect waarmee ze zich onderscheiden. Dat is niet een aspect op individueel niveau, maar een aspect op het niveau van de soort. Asymmetrie komt daarom maximaal tot zijn recht voor aspecten waarvoor geldt dat de ene soort afhankelijk is van de beschikbaarheid van de andere soort, maar niet omgekeerd. Dit modelleert simultaneïteit en dit modelleert dan ook de asymmetrie van de causale relatie: sommige soorten zijn noodzakelijk voor andere soorten (“indien niet…, dan niet”), sommige soorten zijn voldoende voor andere soorten (“indien wel…, dan wel”). In zekere zin is asymmetrie fundamenteler dan symmetrie want we kunnen symmetrie ook modelleren als een wederzijds geldende asymmetrische relatie.

In het symmetrisch geval zijn beide soorten afhankelijk van dezelfde soort (en dat is dus een gelijkaardige asymmetrisch relatie met die soort waarvan ze noodzakelijk afhankelijk zijn): ze onderscheiden zich niet van elkaar op dat aspect en ze treden hiervoor in competitie. Alle biotische factoren zijn afhankelijk van immissie (input of voeding uit een milieu, eventueel abiotisch: de (hulp)bron van hun processen) en emissie (output of excretie in een milieu: de (afval)put van hun processen). Ze zijn dus afhankelijk van het milieu (wat betreft immissie en emissie) maar ze bepalen ook de aard van het milieu (wat betreft immissie en emissie), dus het milieu (en dus ook het medium van communicatie) is afhankelijk van de biologische organismen die er aanwezig zijn. Dat is dus een wederzijds asymmetrische relatie. Bij biotische factoren noemen we de asymmetrie bijvoorbeeld de trofische cascade: sommige soorten zijn noodzakelijke voeding voor andere soorten en wederkerigheid wat betreft het aspect voeding is slechts sporadisch waar te nemen (bijvoorbeeld bij kannibalisme), maar ook mutualisme kan asymmetrisch zijn zoals duidelijk wordt met een voorbeeld: planten worden soms uitsluitend bestoven door diersoorten die zich voeden met nectar of door insecten die stuifmeel verzamelen. Dit maakt de plant afhankelijk van het dier, maar niet omgekeerd omdat het dier zich soms ook kan voeden als die specifieke plant niet aanwezig is. Maar er zijn meer voorbeelden dan enkel de trofische cascade. In een cel bijvoorbeeld zijn verschillende soorten proteïnen aanwezig die noodzakelijk zijn om de structuren te vormen die de cel nodig heeft om zich te (onder)scheiden van zijn milieu en die anders kunnen zijn in telkens weer andere toestanden. Ze worden daartoe gesynthetiseerd of afgebroken afhankelijk van het milieu in en buiten de cel waarin ze zich bevinden. Dit is gemakkelijk vast te stellen doordat de cel zijn eigen celwand produceert waarmee “binnen” en “buiten” van elkaar onderscheiden worden. Wanneer de celwand verbroken wordt, dan komen een aantal proteïnen in een ander milieu terecht en vertonen ze ander gedrag, een nieuw proces start, een gedrag van een andere soort wordt gerealiseerd: een celwand wordt dan misschien terug opgebouwd en zolang het oorspronkelijk milieu niet hersteld is gedragen sommige proteïnen zich anders dan hoe ze zich zouden indien de celwand intact gebleven was, ze zijn in staat van soort te veranderen. Dit is duidelijk een feedback proces in een netwerk van causale (seriële en parallelle) relaties.

De interacties bij de processtappen n kunnen we modelleren door te starten met de vergelijking voor de eenvoudigste cumulatie (het aantal individuen in een groeiende populatie van een bepaalde soort): N_n+1=N_n+ΔN_n+1=N_n+rN_n. We nemen de eigenwaarde r als positief zodanig dat een afnemende populatie van die bepaalde soort gemodelleerd wordt door de vergelijking N_n+1=N_n-ΔN_n+1=N_n-rN_n. De eigenwaarde r noemen we dan ook de verdubbelingstijd en de tijd wordt gemeten in het aantal stappen (elkaar uitsluitende toestanden) die te onderscheiden zijn in het proces (niet noodzakelijkerwijze met eenheid seconde). De eenheid die met die intensiteit gemodelleerd wordt is niet a priori het getal 1 zoals we al begrepen hebben en hebben we als minimaal verschil in het algemeen gemodelleerd als (x-x₀).

We veronderstellen i aantal soorten. Elke soort wordt gekarakteriseerd door zijn eigen procesvergelijking die we van elkaar onderscheiden door de eigenwaarde ±r_i (in praktijk dus de verdubbelings”tijd” of halverings”tijd”), de processtappen zijn dezelfde omdat het de stappen zijn in het proces van interactie in eenzelfde milieu. Er zijn positieve feedback processen en negatieve feedback processen en alle processen zijn begrensd. Zoals er een minimale entiteit kan onderscheiden worden die niet meer in kleinere stappen kan verdeeld worden (bijvoorbeeld gehalveerd worden), zo kan er ook een maximale entiteit onderscheiden worden die niet meer kan toenemen (bijvoorbeeld verdubbelen). Het verschil tussen de populaties noteren we dus als een index i. Hiermee vermijden we ook a priori interpretaties van de soorten. A priori leiden er dikwijls toe dat soorten louter als input, (hulp)bron of als output, (afval)put gezien worden. Immissie en emissie, (hulp)bron en (afval)put zijn relatieve begrippen die afhankelijk zijn van het beschouwde proces, wat we bestuderen en modelleren is een relativiteit van gekozen processen. Bijvoorbeeld: sommige soorten gebruiken afval van andere soorten als hulpbron voor hun eigen metabolisme en ze emitteren een ander soort hulpbron die ze zelf als afval beschouwen, terwijl ze wellicht ook nakomelingen emitteren. Daarenboven willen we ook hiermee bespreekbaar maken dat zowel input als output gewenst kan zijn of niet, er is daar niets absoluuts aan.

We geven een voorbeeld met slechts 2 soorten. Dit is uiteraard uit te breiden naar meerdere soorten.

N_1,n+1=N_1,n+ΔN_1,n+1=N_1,n+r₁N_1,n

N_2,n+1=N_2,n+ΔN_2,n+1=N_2,n+r₂N_2,n

We onderscheiden een asymmetrische en symmetrische beïnvloeding. Bij een asymmetrische relatie spelen de beide soorten een tegengestelde rol. Bij een symmetrische relatie spelen de beide soorten een zelfde rol. Zoals bij de negatieve en positieve feedback zouden we dat grafisch kunnen voorstellen door verbindende lijnen tussen de twee gekwantificeerde buffers, we gebruiken dan stippellijnen wanneer de aantallen in de buffers in tegengestelde richting veranderen, we gebruiken dan volle lijnen wanneer de aantallen in de knooppunten in dezelfde richting veranderen. Dus als formule zien we dan in het asymmetrisch geval N_1,n+1=N_1,n+r₁N_1,n en N_2,n+1=N_2,n-r₂N_2,n of N_1,n+1=N_1,n-r₁N_1,n en N_2,n+1=N_2,n+r₂N_2,n. In het symmetrisch geval zien we N_1,n+1=N_1,n+r₁N_1,n en N_2,n+1=N_2,n+r₂N_2,n of N_1,n+1=N_1,n-r₁N_1,n en N_2,n+1=N_2,n-r₂N_2,n. Zoals we ook begrepen hebben voor negatieve en positieve feedback, moeten niet nog meer mogelijkheden onderscheiden worden, de effecten zullen enkel van het aantal lijnen van een van de twee mogelijke soorten lijnen afhangen.

Beïnvloeding door de intensiteit aan individuen in twee buffers kunnen we modelleren door aantallen van de andere soort in de vergelijking van elke soort binnen te brengen. De aantallen ondersteunen of begrenzen dan elkaar, eventueel slechts in een beperkt gebied. Dan zal de Δn_i,n term niet alleen afhankelijk zijn van de eigen eigenwaarde en de eigen intensiteit, maar ook van (het product van) de twee aantallen, dus Δn_i,n∝ΔN_1,nN_2,n en dat voor de twee soorten. Het product modelleert simultaneïteit, wat we op zijn coherentie onderzocht hebben met de evaluatie van een relatie (x-x₀)Π_ν(1+κ) op het punt n en k, waarbij zowel ν als κ variabelen zijn. De parameter ν kan enkel toenemen, de parameter κ kan toenemen en afnemen in het interval tussen -1 en +1, en dus negatieve of positieve feedback modelleren. Het aantal soorten (parameter κ) is altijd kleiner dan ν.

Als we meerdere vergelijkingen gebruiken in een model hoeft dit uiteraard niet te betekenen dat alle mogelijke producten van Δn_i,n termen zinvol zijn.

Simultaneïteit is een heel belangrijk inzicht dat zelden expliciet vermeld wordt: we modelleren wel evolutie in een aantal stapen maar de interacties zijn “simultaan aanwezig” (dit is wat door het product gemodelleerd wordt en door een gesloten lus in de grafische voorstelling van een netwerk van buffers) en de interacties zijn hierdoor causaal verbonden met de aantallen. De interacties die door een product gemodelleerd worden zijn “onafhankelijk van de geschiedenis” (dit is wat men “de Markov eigenschap” noemt).

Asymmetrische beïnvloeding

Eerst bespreken we de asymmetrische relatie van twee soorten. Het is dus de product term Δn_1,nN_2,n die voor asymmetrie moet zorgen. Die asymmetrie is dat er bij interactie tussen beide soorten, de individuen in de ene soort afnemen als de individuen in de tweede soort toenemen, maar als een soort “mogelijkheid voor simultane aanwezigheid” overschreden wordt (de “draagkracht van het milieu voor twee soorten”) zullen de individuen in de tweede soort afnemen zodanig dat de individuen in de eerste soort terug toenemen. Deze interpretatie van “draagkracht” zal verder nog duidelijk worden en een grote rol spelen. We modelleren de interactie als volgt met een k₁₂ en een k₂₁:

N_1,n+1=N_1,n+ΔN_1,n+1=N_1,n+r₁(N_1,n-k₁₂N_1,nN_2,n)

N_2,n+1=N_2,n+ΔN_2,n+1=N_2,n-r₂(N_2,n-k₂₁N_1,nN_2,n)

De Δ die in beide vergelijkingen gemodelleerd wordt heeft een term die geen product is van aantallen (namelijk r_i(N_i,n)) en een term die een product is (namelijk r_ik_ijN_i,nN_j,n in het ene geval en r_ik_jiN_i,nN_j,n in het andere geval). De interpretatie van deze relatie als “mogelijkheid voor simultane aanwezigheid” zullen we nu verduidelijken en we zullen begrijpen waarom we een verschil moeten maken tussen een eenheid en zijn intensiteit.

We herschrijven de eerste vergelijking: N_1,n+1=N_1,n+r₁(N_1,n-k₁₂N_1,nN_2,n) als N_1,n+1=N_1,n+r₁N_1,n(1-k₁₂N_2,n) en we veronderstellen dat N_1,n=N_2,n. De vergelijking heeft dan het formaat N_1,n+1=N_1,n+r₁N_1,n(1-N_1,n/K₁₂) waarin we de Verhulst vergelijking herkennen met k₁₂=1/K₁₂, hierin speelt K₁₂ de rol van “de draagkracht van het milieu voor soort₁”. Dit wordt als volgt duidelijk: de Verhulst vergelijking met r₁<1 hebben we als logistische differentievergelijking onderzocht en dan hebben we begrepen dat de extrema in dit proces (N_1,n=0 en (1-N_1,n/K₁₂)=0) nooit bereikt kunnen worden als gevolg van een processtap want N_1,0 is niet anders dan de eenheid van soort₁. Die eenheid is voor een soort gewoonlijk meer zijn dan 1 want voor veel soorten zijn individuen niet in staat zich te reproduceren en is een minimale populatie noodzakelijk van verschillende ondersoort in soort. We kunnen nu veronderstellen dat er geldt dat N_1,n=K₁₂ want dan modelleren we dat er geen toename meer is en dus dat evenwicht bereikt is (ΔN_1,n+1=0 want N_1,n+1=N_1,n). Evenwicht voor twee vergelijkingen zullen we verder heel precies modelleren en dat is nu even niet de focus. Wat het model N_1,n+1=N_1,n toont is dat de grens van de waarnemingsresolutie bereikt is, namelijk de ordening van toename of afname is verdwenen. Zuiver wiskundig krijgen we bij elke stap wel een ander getal (en er geldt niet dat N_1,n+1=N_1,n) maar dat getal is zodanig klein dat het niet kan modelleren dat er een eenheid bijgekomen of afgegaan zou zijn. Veronderstel dan dat het mogelijk is dat N_1,n>K₁₂ met minstens één eenheid. Het model laat dan zien dat er “abrupt” een nieuw proces gestart wordt met een negatieve eigenwaarde (want de term (1-N_1,n/K₁₂) is dan negatief) en een nieuwe eenheid, de maximale populatie, N_1,n=K₁₂ die in de volgende stappen enkel verder kan afnemen. Dat is natuurlijk gelijkaardig voor een proces van negatieve feedback die dan plots verandert naar een positieve feedback. Dat is de betekenis van “draagkracht”: boven (onder) een bepaalde grenswaarde verandert het proces van positieve (negatieve) in een negatieve (positieve) feedback en er ontstaat eventueel periodiciteit. De causale relatie die dan werkt kunnen we als volgt beschrijven: de toename van de populatie met één eenheid neemt de noodzakelijke aanwezigheid van een (hulp)bron weg of zorgt voor voldoende afval die niet meer in een put kan verdwijnen. Deze mogelijkheden zijn een disjunctie, geen exclusieve disjunctie. Maar dit maakt ook duidelijk wat de betekenis is van de twee aantallen K₁₂ en K₂₁: zij hoeven geen constanten te zijn en ze zijn evenzeer aan verandering onderhevig. We hebben ze “draagkracht” genoemd en dit is voldoende abstract om K₁₂ en K₂₁ als kwantitatieve output van sommige “buffers” van een zeer uitgebreid netwerk van knooppunten te beschouwen (knooppunten waartussen relaties gelden die de knooppunten maken tot relatieve (hulp)bronnen en (afval)putten). In de volgende vorm zijn de vergelijkingen dus iets meer sprekend:

N_1,n+1=N_1,n+ΔN_1,n+1=N_1,n+r₁(N_1,n-(1/K₁₂)N_1,nN_2,n)

N_2,n+1=N_2,n+ΔN_2,n+1=N_2,n-r₂(N_2,n-(1/K₂₁)N_1,nN_2,n)

Stel N_2,n=K₁₂, dan is ΔN_1,n+1=0

Stel N_1,n=K₂₁, dan is ΔN_2,n+1=0

Als abstract patroon voor Δn_i,n+1 kunnen we dus de vormen onderscheiden:

Δn_i,n+1 kan niet gelijk zijn aan nul voor:

Δn_i,n+1=±r_i(N_i,n)

Δn_i,n+1=±r_i((1/K_ij)N_i,nN_j,n)

Δn_i,n+1 kan wel gelijk zijn aan nul voor:

Δn_i,n+1=±r_i(N_i,n-(1/K_ij)N_i,nN_j,n)

Eens we het abstracte asymmetrisch model voldoende begrepen hebben kunnen we veel voorbeelden geven van processen met asymmetrische relatie door de eigenwaarden r_i en bijkomende parameter k_ij met verschillende en uiteenlopende historisch ontstane concepten te interpreteren.

1. We nemen “prooien” (of biotische factor, flora, fauna) als soort₁ en “natuurlijke vijanden van de prooien” (of biotische factor, grazer, parasiet, predator, ...) als soort₂. Prooien zijn ook predatoren van een soort, ze halen hun voeding (immissie) uit hun omgeving (binnen de grenzen van de draagkracht die voor de voeding zorgt) en dan groeit hun populatie (emissie), dus +r₁ kan dat modelleren. Als er geen prooien zijn, dan hebben de natuurlijke vijanden geen voedsel en neemt hun populatie af, dus -r₂ kan dat modelleren. Natuurlijke vijanden (of parasieten) vallen prooien aan en dan neemt het aantal prooien af (of een individueel aspect van een prooi kan minder groeien), dus -r₁k₁₂ kan dat modelleren. Het is niet voldoende dat natuurlijke vijanden prooien als voeding (immissie) gebruiken, ze moeten ook in staat zijn met dat voedsel voor nageslacht te zorgen (emissie) en enkel zo kan hun aantal toenemen (en voor parasieten is dat trouwens evident), dus +r₂k₂₁ kan dat modelleren.

2. We modelleren met een asymmetrische relatie ook infecties. We noemen een niet geïnfecteerde soort soort₁ en we noemen soort₂ de geïnfecteerde populatie van soort₁. Zolang er zowel een normale populatie is als een geïnfecteerde populatie, neemt de geïnfecteerde populatie toe, dus +r₂k₂₁ kan dat modelleren. De normale populatie neemt dan af en dat wordt gemodelleerd door -r₁k₁₂. De geïnfecteerde populatie kan zich herstellen tot een nieuwe normale populatie (en dan bijvoorbeeld immuun worden voor de infectie zodanig dat soort₂ volledig verdwijnt), dus +r₁ kan dat modelleren. De geïnfecteerde populatie neemt dan af, dus -r₂ kan dat modelleren. Dit is een dynamisch proces wanneer de eigenwaarden r_i, k_ij en k_ji samen evolueren.

3. We hebben immissie al als voeding geïnterpreteerd en emissie als de productie van nageslacht. Emissie van persistente factoren, dikwijls abiotische factoren die dan immissie zijn voor sommige soorten kunnen we ook pollutie noemen. Pollutie kan dan als infectie gemodelleerd worden en persistente pollutie is pollutie waarvan de populatie zich niet kan herstellen omdat het daarvoor de processen (nog) niet heeft ontwikkeld.

4. Besmettelijke informatiepatronen worden bestudeerd in de memetica.

5. Infectie en pollutie hebben de connotatie van iets dat vermeden moet worden, maar we kunnen ook voorbeelden geven die meer neutraal of zelfs gewenst zijn. Noem bijvoorbeeld de soort₁ mensen die (nog) niet gemotiveerd zijn door een bepaald verhaal en de soort₂ zijn dan mensen die dit wel zijn. In een productiecontext kunnen we dat concreet maken door de soort₁ te beschouwen als de normale productieomgeving en soort₂ te beschouwen als de groep die aan kwaliteitszorg werkt (het dagelijks gewenste gevecht om in de veranderende omgeving op verschillende niveaus van complexiteit causale patronen te distilleren uit metingen aan producten zodanig dat de bedoelde specificaties kunnen behouden worden en aanpassing naar andere specificaties kunnen uitgevoerd worden wanneer de omgeving verandert door andere producten, andere eisen, andere markten enz...). Er worden dan verschillende soorten taken uitgevoerd door beide soorten. Zoals we in praktijk dikwijls kunnen vaststellen kan de toename van soorten taken contraproductief worden en degenereren in een steeds toenemende controle van controle op controle die geen waarde meer toevoegt. Typisch in dit verband is administratie die (“helaas”) de complexiteit van taken verhoogt, of de doorgedreven automatisatie van taken die verder niet meer in vraag gesteld worden. Hetzelfde zien we ook gebeuren in een causaal gesloten economie: de relaties zijn deze van leveranciers en afnemers die wederzijds van elkaar afhankelijk zijn. Het resultaat is een periodiciteit die goed kan gedocumenteerd worden.

6. In een cel gaan er voortdurend processen door die specifieke proteïnen genereren. Sommige van die proteïnen die in de nabijheid van de celwand komen worden vervormd door de spanning in de celwand en dank zij die vervorming kunnen ze door de celwand geïntegreerd worden. De proteïnen in de celwand noemen we nu soort₁ en de proteïnen in de cel soort₂. De celwand haalt zijn individuele cellen uit de cel en dat kan alleen maar als de cel intact is en dus een celwand heeft. Soort₁ heeft soort₂ nodig en soort₂ heeft soort₁ nodig. Dit is dus een voorbeeld van twee asymmetrische relaties die samen een symmetrie vormen. Als de cel groeit moet de celwand volgen, dat kan omdat de spanning in de celwand dan toeneemt en dus meer proteïnen vervormd worden, dus +r₁ kan dat modelleren (de celwand maakt meer cellen). Als het aantal cellen in de cel om de een of andere reden afneemt dan krimpt de cel, dus -r₂ kan dat modelleren (en de celwand moet volgen). De cel kan ook proteïnen uit de celwand recycleren als ze niet meer onder spanning (vervorming) staan en dan wordt de celwand kleiner, dus -r₁k₁₂ kan dat modelleren. Als de juiste proteïnen aanwezig zijn dan kan de cel groeien en het totaal aantal proteïnen neemt toe, dus +r₂k₂₁ kan dat modelleren.

Het is duidelijk dat elke concrete situatie met meerdere soorten met eigenwaarde r_i meerdere soorten producten van de betrokken intensiteiten zal moeten kunnen onderscheiden en dat er meerdere parameters k_i...j...k zullen nodig zijn die causale interactie van specifieke soorten (producten met meer dan twee termen) met elkaar verbindt.

Evenwicht voor twee soorten

De vergelijkingen geven ons de voorwaarden waarbij evenwicht bereikt wordt, dat is wanneer ΔN_i,n+1 gelijk is aan nul, zowel voor soort₁ als voor soort₂.

Voor soort₁:

ΔN_1,n+1=r₁(N_1,n-k₁₂N_1,nN_2,n)=0

N_1,n=k₁₂N_1,nN_2,n

1/k₁₂=N_2,n

K₁₂=N_2,n

Evenwicht voor soort₁ hangt enkel af van het aantal van soort₂.

Voor soort₂:

-r₂(N_2,n-k₂₁N_1,nN_2,n)=0

N_2,n=k₂₁N_1,nN_2,n

1/k₂₁=N_1,n

K₂₁=N_1,n

Evenwicht voor soort₂ hangt enkel af van het aantal van soort₁.

Bij evenwicht zijn verhoudingen aan elkaar gelijk, namelijk k₁₂N_2,n=k₂₁N_1,n (of N_1,n/K₂₁=N_2,n/K₁₂), dus de aantallen zijn elkaars draagkracht.

Merk op dat evenwicht niet mogelijk is als de intensiteit van een soort gelijk is aan nul, wat inderdaad een goede modellering is van de werkelijkheid van een soort die afhankelijk is van een andere. Als er geen prooien zijn, dan sterven ook de parasieten uit en als er geen parasieten zijn nemen de prooien exponentieel toe of af tot de draagkracht van het milieu, eventueel verdwijnt de overblijvende populatie ook als de draagkracht toch overschreden wordt. Meerdere soorten zijn dus noodzakelijk om een evenwicht te bereiken dat de draagkracht van het milieu voor twee soorten vormgeeft. Dat evenwicht zal altijd dynamisch zijn. Daarenboven hebben we nu bewezen dat een evenwicht in principe altijd mogelijk is omdat de parameters k₁₂ en k₂₁ a priori niet afhankelijk zijn van eigenwaarden r₁ of r₂. In de praktijk betekent dit dus dat een parasitaire soort zijn effectiviteit in principe kan aanpassen aan de groeisnelheid van de soort waarop het parasiteert, en dat de soort waarop geparasiteerd wordt zijn groeisnelheid kan aanpassen aan de effectiviteit van de parasiet. Dit is ook duidelijk met het voorbeeld van de infectie en dit is ook duidelijk in het voorbeeld van de cel en de celwand. Dit is dan een mutualistische symbiose. Beide kunnen met elkaar leven en ze kunnen zelfs gedurende veel processtappen een stabiele intensiteit van individuen bereiken. Die intensiteit ligt niet in principe vast maar wordt wel beperkt door de intensiteit van de andere soort.

Simulatie

We kunnen nu enorm veel patronen maken in een kwantitatieve simulatie. We moeten wel opletten dat de simulaties respect hebben voor het verschil tussen intensiteiten en entiteiten. Bijvoorbeeld: wanneer de intensiteit van een soort beneden de levensvatbare intensiteit gaat, dan hebben we eigenlijk met een aantal te maken dat de entiteit zelf karakteriseert (dus de soort), en niet alleen zijn intensiteit. Een soort wordt bepaald door een levensvatbaar minimum (bijvoorbeeld minimaal een vertegenwoordiger van elk geslacht), dat is wel “een aantal” maar het heeft de karakteristiek van “een entiteit”, iets dus dat niet kan gehalveerd worden (het minimum) of iets dat niet kan verdubbeld worden (het maximum). Dit “minimum (maximum) aantal individuen” van een soort ligt niet a priori vast, maar is ook afhankelijk van het milieu (de aanwezigheid van voedsel, belagers, risicogedrag enz…). Dit is overduidelijk in het voorbeeld van de cel: een minimale cel heeft een complex aan proteïnen en enzymen en heeft een minimale celwand en de organisatie van de cel moet zodanig zijn dat dit complex en de celwand bestendigd worden. Een ander voorbeeld is de minimale complexiteit van een autonome economie. De simulatie zal dus minstens een logische redenering moeten bevatten van het type “indien een aantal kleiner is dan x, dan is er geen verschil met een aantal gelijk aan nul”. Dit is de grens van de resolutie. Dit geldt voor de bovengrens en de ondergrens. De parasiterende soort zal dan geen voeding meer kunnen vinden of de cel zal dan niet meer kunnen overleven. Beide soorten, samen met de gedeelde context en de niet gedeelde context kunnen een nieuwe entiteit gaan vormen waarbij geldt dat sommige intensiteiten “niet meer kunnen gehalveerd worden of niet meer kunnen verdubbeld worden” in een negatieve of positieve feedback.

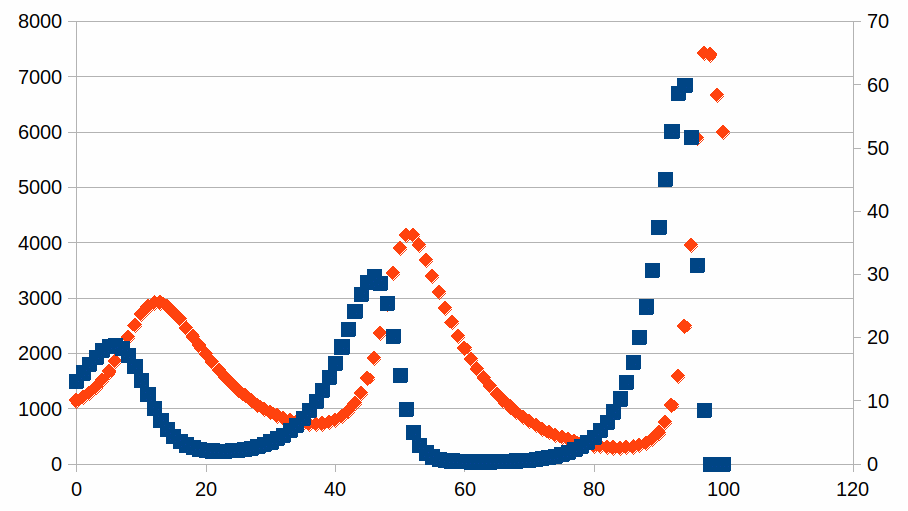
Hieronder een voorbeeld met de evolutie van twee populaties gedurende 100 stappen in de abscis: de ordinaat voor vierkante datapunten gebruikt de schaal aan de linkerkant van de grafiek, de ordinaat voor de ruit datapunten gebruikt de schaal aan de rechterkant van de grafiek. Het startpunt is dus een populatie van 1500 voor de soort₁ en een populatie van 10 voor de soort₂. De startpunten zijn willekeurig gekozen. De tweede soort kunnen we interpreteren als een parasiet van de eerste soort. Het schaalverschil is zeer typisch. We plotten de volgende vergelijkingen:

N_1,n+1=N_1,n+ΔN_1,n+1=N_1,n+0,3(N_1,n-(1/15)N_1,nN_2,n)

N_2,n+1=N_2,n+ΔN_2,n+1=N_2,n-0,1(N_2,n-(1/1000)N_1,nN_2,n)

De parameters k_i,j en k_j,i geven we weer in het “draagkracht”-patroon. Zo wordt het verschil van aantallen in de evenwichtssituatie onmiddellijk duidelijk: stel dat we met de beginaantallen N_1,0=1000 en N_2,0=15 zouden starten dan zouden we geen evolutie van aantallen zien.

De evolutie van beide aantallen is gekoppeld en vertoont het patroon van een golf en dus periodiciteit van intensiteiten. Zoals bekend bij golfverschijnselen induceert dit de mogelijkheid tot resonantie van golven en daardoor met grote waarschijnlijkheid grote schommelingen in een milieu met een overvloed aan periodische processen en dus nog meer gekoppelde evoluties.

De evolutie van beide aantallen kunnen we ook visualiseren als een plot met koppels (soort₁; soort₂): het startpunt is het punt (1500; 10), het volgende punt is (1650; 10,5) en zo verder, en zo wordt de curve in tegenwijzerzin doorlopen bij het toenemen van het aantal processtappen.

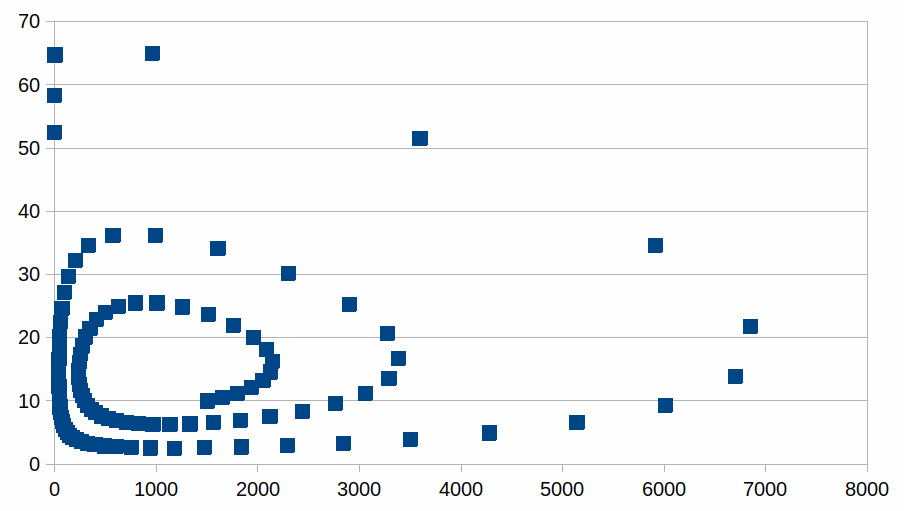
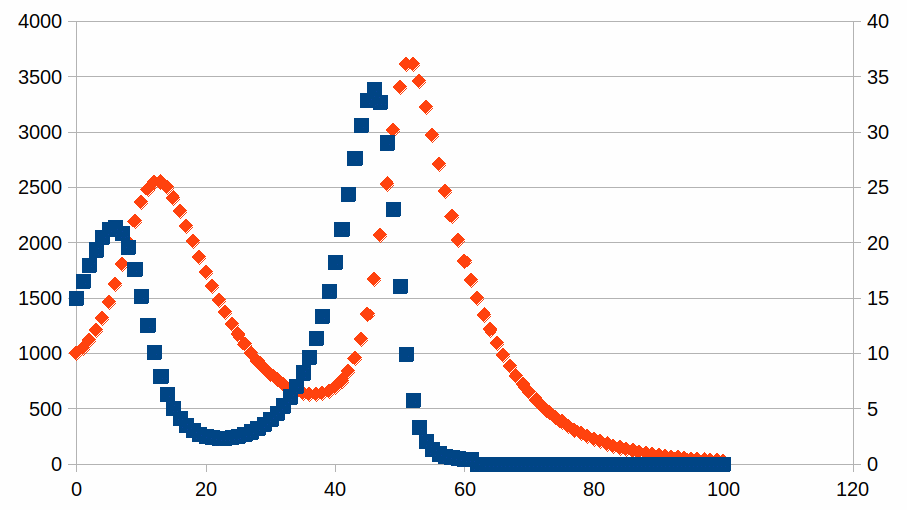
De curve is een voorbeeld van een attractor in een dynamiek. Wat ook het aantal individuen is in de koppels, er is een relatie tussen beide, met periodes van relatieve stabiliteit voor een van de soorten, afgewisseld met periodes van grote veranderingen zonder dat er ooit evenwicht bereikt wordt. We kunnen zien op de grafiek dat de intensiteiten zich steeds verder verwijderen van het evenwichtspunt (1000, 15). Het is dus mogelijk dat een van de soorten volledig verdwijnt van zodra er een situatie bereikt wordt waarin het aantal individuen zo laag is dat het aantal niet meer kan afnemen noch toenemen. Maar we weten amper welke processen en welke entiteiten nodig zijn in een hele ecologie om zichzelf te kunnen onderhouden en we hebben een zeer slecht zicht op “wat” de eenheid is van een soort waarvan we een intensiteit (populatie) waarnemen. Hieronder een grafiek voor de evolutie waarin de leefbare populatie van soort₁ niet nul is maar 40, eens de populatie kleiner is dan 40 individuen wordt ze helemaal opgeslokt door soort₂, die dan natuurlijk ook verdwijnt.

Zoals de beide grafieken tonen voor de evolutie van soort₁, is het niet ongewoon dat het verdwijnen van een populatie veel sneller gaat dan de opbouw ervan (dit wordt het Seneca effect genoemd en werd gepopulariseerd door Ugo Bardi). Voor de evolutie van soort₂ zien we ook een asymmetrie in de twee grafieken, maar het tegenovergestelde: de opbouw is veel sneller dan de afbraak.

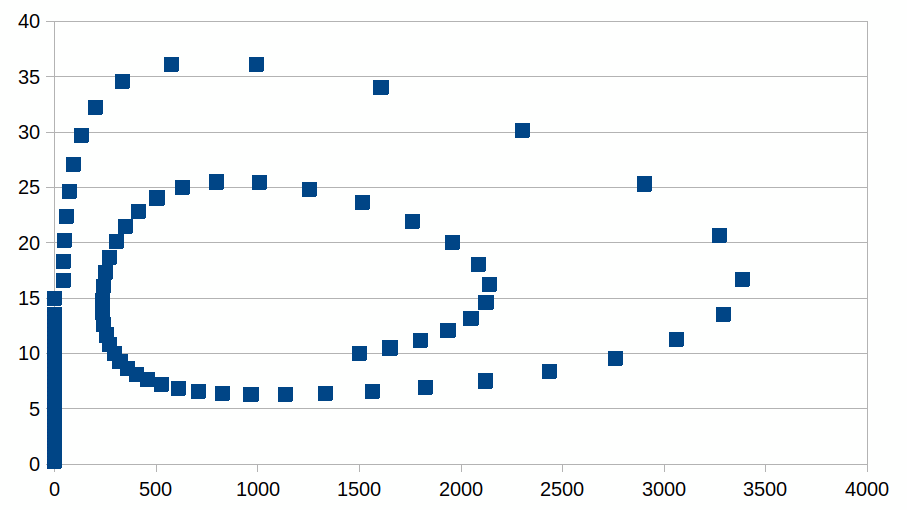
De attractor geeft aan de dynamiek een identiteit, het maakt ervan “een soort”, “een entiteit” omdat sommige koppels in deze abstracte ruimte nooit zullen kunnen bereikt worden, ze sluiten elkaar uit (de conjunctie van beide aantallen heeft waarde “neen”). We kunnen dus spreken van een soort dynamiek en verschillende dynamieken zouden dan ook in competitie of resonantie kunnen staan.

Symmetrische beïnvloeding

Het product van twee aantallen, dus ΔN_n∝ΔN_n,1N_n,2, kunnen we ook construeren met maar één soort. Dat doen we wanneer we de interacties bij de processtappen n modelleren door als basis de Verhulst vergelijking te nemen voor het aantal individuen in de populatie: N_n+1=N_n+ΔN_n+1=N_n+rN_n(1-N_n/K). Hierin vinden we expliciet de draagkracht terug “die voor immissie en emissie zorgt”. Het product van de aantallen zien we in de term rN_nN_n/K.

Elke soort heeft zijn eigen vergelijking aangezien zowel de eigenwaarde als de draagkracht zullen verschillen, we noteren dat met een index.

N_1,n+1=N_1,n+r₁N_1,n(1-N_1,n/K₁₂)

N_2,n+1=N_2,n+r₂N_2,n(1-N_2,n/K₂₁)

Nu kunnen we de invloed van soort₂ op soort₁ modelleren door in te zien dat de groei van soort₁ intrinsiek beperkt wordt door de toename zelf van het aantal individuen van soort₁ (dit verklaart de term -N_1,n/K₁₂). In aanwezigheid van een concurrerende soort wordt de groei van soort₁ dus ook beperkt door een aantal individuen van soort₂ en dit kunnen we nu modelleren door een term -α₁₂N_2,n/K₁₂. Hierin staat α₁₂/K₁₂ voor de invloed van soort₂ in de context van soort₁. Het ligt voor de hand om ook een term α₂₁/K₂₁ te onderscheiden die de invloed van soort₁ in de context van soort₂ kan modelleren en zo de symmetrische beïnvloeding uitdrukt.

Dit resulteert in de twee vergelijkingen van het model van symmetrische beïnvloeding:

N_1,n+1=N_1,n+r₁N_1,n(1-N_1,n/K₁-α₁₂N_2,n/K₁₂)

N_2,n+1=N_2,n+r₂N_2,n(1-N_2,n/K₂-α₂₁N_1,n/K₂₁)

De vergelijkingen maken ook duidelijk dat hogere machten van N_i,n met hun eigen parameter α zinvol kunnen zijn. Dit genereert dan een veelterm in verschillende variabelen.

Evenwicht voor twee soorten

De vergelijkingen geven ons de voorwaarden waarbij evenwicht bereikt wordt, dat is wanneer ΔN_i,n+1 gelijk is aan nul. We onderzoeken dat zowel voor soort₁ als voor soort₂.

Voor soort₁:

r₁N_1,n(1-N_1,n/K₁-α₁₂N_2,n/K₁₂)=0

1=N_1,n/K₁+α₁₂N_2,n/K₁₂

K₁=N_1,n+α₁₂N_2,nK₁/K₁₂

N_1,n=K₁(1-α₁₂N_2,n/K₁₂)

Dus voor soort₂ geldt volledig gelijkaardig:

N_2,n=K₂(1-α₂₁N_1,n/K₂₁)

Beide geven een lineair verband tussen de aantallen. Dit betekent dat er voor elk aantal van een soort die gekarakteriseerd wordt door een draagkracht K_ij, er een aantal te vinden is van de andere soort dat daarmee in evenwicht is, als de soort zijn impact α kan aanpassen. Maar dat betekent ook dat elke soort in staat is de populatie van de andere soort tot nul te reduceren door zijn impact α aan te passen. Dat zien we dus ook in werkelijkheid en dat blijkt dan de enige mogelijkheid te zijn om soorten uit te roeien zonder zelf als soort te verdwijnen (in het asymmetrisch geval is dat onmogelijk voor de soort die afhankelijk is van de andere).

Als we dit besluit vergelijken met het besluit bij de asymmetrische situatie dan is duidelijk dat draagkracht de fundamentele beperking is, niet het samenleven met parasitaire soorten (“meelifters”, “meelopers”, “free-riders”, “profiteurs”, ...) waarvan het aantal nooit tot nul kan gereduceerd worden, omdat elke soort onvermijdelijk “parasiteert” op een (dikwijls onuitputtelijk geachte) bron en een (dikwijls bodemloos geachte) put als ultieme beperkingen van de draagkracht. Maar dat betekent ook dat parasiteren en geparasiteerd worden voor een soort de enige waarborg is om als soort niet te verdwijnen: parasitaire soorten gebruiken andere soorten als (partiële) bron voor overleven, andere soorten die een noodzakelijke grondstof leveren (of een levensnoodzakelijke afscherming of een levensnoodzakelijke emissie mogelijkheid of voor een bepaald aspect een grotere draagkracht hebben in een bepaald milieu). De populatie van de ene soort zal onvermijdelijk een veel kleinere schaal hebben dan de populatie van de andere soort.

Het dynamisch evenwicht van populaties is mogelijk door de impact die beide soorten op elkaar hebben. Ze moeten daartoe een onderscheidingen universum delen. Dus draagkracht moeten we dan ook begrijpen als beperking op sporen die kunnen ontstaan. Enkel wanneer processen sporen produceren in hetzelfde medium, sporen die door meerdere soorten relevant bevonden worden, dan kunnen ze in competitie treden met elkaar (exclusieve disjunctie) of kan er symbiose of synergie ontstaan.

Simulatie

Ook nu kunnen we een a priori onbeperkt aantal patronen maken in een kwantitatieve simulatie. Hierbij een voorbeeld waarbij twee populaties dezelfde grens hebben van draagkracht (namelijk 1000), maar gestart wordt in de ene populatie met 100 en de andere populatie met 50 met een eigenwaarde van de eerste die het dubbele is van de eigenwaarde van de tweede. Er wordt een stabiliteit bereikt met een totaal aantal individuen groter dan de draagkracht van slechts één soort.

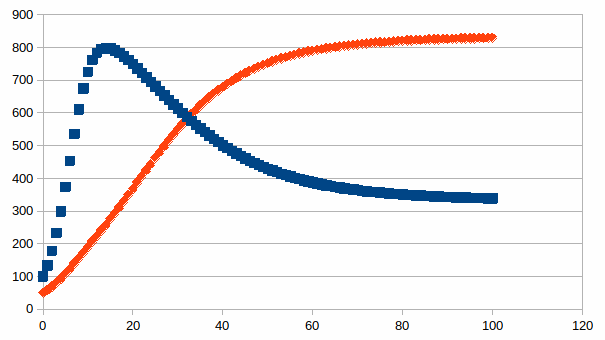
Beide populatie aantallen zijn op de volgende manier met elkaar gerelateerd, de lineaire verbanden die evenwicht begrenzen zijn visueel te herkennen:

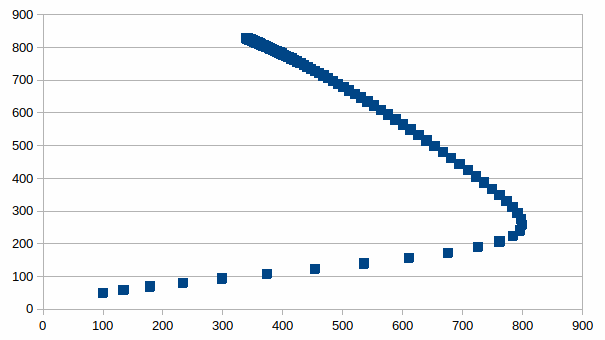
Een simulatie die een van de soorten volledig elimineert is door een voldoende hoge waarde van α₁₂ als volgt te visualiseren:

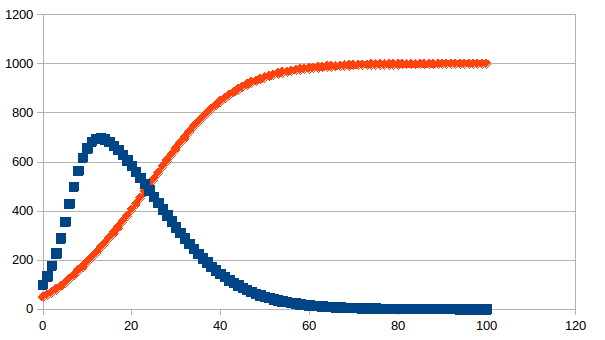
De relatie tussen beide populaties is dan:

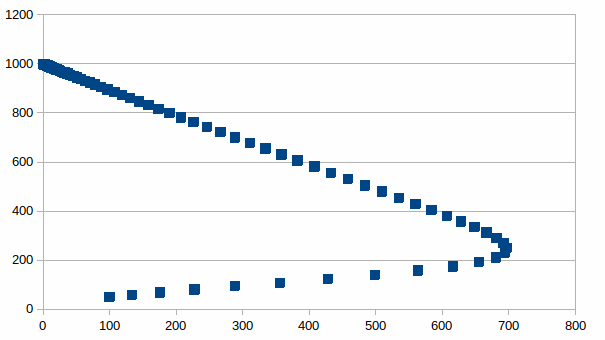
Het is opmerkelijk dat de som van het aantal individuen groter is als er meer soorten zijn die in hetzelfde milieu een andere draagkracht hebben. De som is maximaal wanneer het aantal individuen per soort gelijk is, zoals in de onderstaande grafiek:

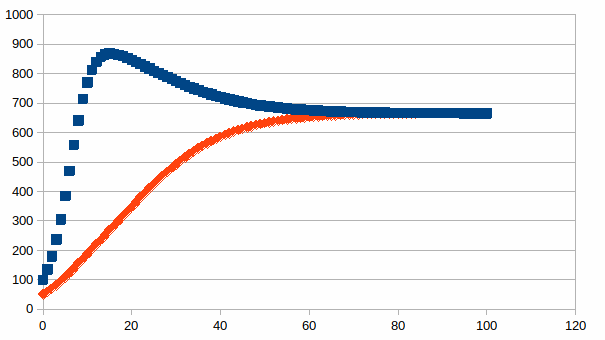
Dit is een verklaring voor de veerkracht van het samenspel van meerdere soorten met een onvermijdelijk beperkte draagkracht. Om dit samenspel te beschrijven wordt in de ecologie het begrip “niche” gebruikt. De competitie van soorten voor dezelfde bronnen bevoordeelt specialisatie tussen soorten zodanig dat ze in verschillende habitats kunnen overleven die gezien worden als deelgebieden van een grote gedeelde habitat. Hierdoor moeten de soorten geen energie mee investeren om in competitie te treden met elkaar en wordt de fundamentele energiestroom die door de zon geleverd wordt maximaal omgezet in materie. Niches in de ruimte (plaatsen met andere karakteristieken) worden ook onderscheiden van niches in de tijd (andere karakteristiek in <<dag versus nacht>>, seizoenen enz…).

Gevolg: verbeelding, intelligentie, aanpassingsvermogen

De som van het aantal individuen (de intensiteit van de eenheid “soort”) is maximaal wanneer het aantal individuen per soort met verschillende draagkracht gelijk is. Dit verklaart het evolutionair voordeel van individuen die dank zij hun verbeelding en inleving de rol kunnen spelen van verschillende soorten met verschillende draagkracht, en hiermee getuigen van verbeelding, intelligentie en aanpassingsvermogen. Het aanpassingsvermogen door soorten₁ aan de aanwezigheid van andere soorten₂ hebben we gemodelleerd door de getallen k₁₂, k₂₁, α₁₂, α₂₁. Indien een aantal entiteiten verschillende rollen kunnen spelen, afhankelijk van de eisen van het milieu, dan verhoogt de overlevingskans van dit bepaald aantal (dus zelfs als het aantal niet gewijzigd wordt en zich in evenwicht bevindt). Dat is een typische karakteristiek van de toppredatoren in een ecosysteem die bijvoorbeeld in staat zijn de vruchtbaarheid van de populatie aan te passen aan de beschikbaarheid van voedsel. Het aanpassingsvermogen is niet anders dan de mogelijkheid om “van soort” te veranderen zowel in ruimte als in tijd. Bij elke evolutie moeten we immers een verschil maken tussen twee soorten evolutie: de evolutie van een intensiteit en de evolutie van een eigenwaarde als een soort entiteit. De evolutie van een eigenwaarde kan de evolutie modelleren “in het universum van soorten”, de evolutie van de intensiteit kan de evolutie modelleren van de aantallen binnen die soorten. Beide evoluties kennen een andere schaal, enerzijds een aantal eenheden (logische combinaties van onderscheidingen), anderzijds een intensiteit van die eenheden (te kwantificeren als een laatst toegevoegde onderscheiding die de eenheden zelf niet wijzigt).