Entiteiten (eenheden, soorten die elkaar uitsluiten, …) zijn onvermijdelijk begrensd. Niet a priori begrensd is de intensiteit van een entiteit, het kwantum van de eenheid.

Maar voor veel entiteiten is ook de intensiteit begrensd, het kwantum heeft onvermijdelijk een ondergrens maar (misschien niet onvermijdelijk) ook een bovengrens. Dikwijls is dat vast te stellen doordat de aantallen entiteiten een sigmoïde relatie hebben met het aantal stappen in een proces dat hun aantal bepaalt. Dat is dus een discontinue verandering. Een typisch voorbeeld hiervan is de populatie van een biotische soort: enerzijds is er minimaal één individu (anders is er niets te tellen), anderzijds zijn er maximaal N individuen mogelijk in een bepaald milieu. De sigmoïde relatie herkennen we doordat bij de eerste processtappen het aantal individuen exponentieel toeneemt (afneemt) tot een punt bereikt is van maximale toename (afname), waarna een exponentiële afname (toename) start waarbij een maximum (minimum) nooit overschreden wordt. De curve van de aantallen per stap is dan S-vormig (of Z-vormig) tussen 0 en N. We kunnen dat interpreteren als het spontaan ontstaan van een nieuwe entiteit: een “populatie in interactie in en met een milieu”.

Wiskundigen die de S-curve zagen gingen er dan van uit dat daarvoor een logistische relatie kon gevonden worden, maar dat bleek niet evident doordat theoretische wiskundigen eigenlijk niet geïnteresseerd zijn in het maken van een opsplitsing tussen aantallen en eenheden (“in de limiet...”). Praktische wiskundigen zijn dan “logistische differentievergelijkingen” gaan bestuderen. Een van die mogelijke differentievergelijkingen is iconisch geworden omdat het een voorbeeld is geworden van deterministisch chaotisch gedrag. Een abstracte vergelijking voor de toename (afname) bij één stap is de volgende: ΔN_t+1=N_t(a-bN_t). Voor b=0 is dat niet anders dan een exponentieel verband dat we uitgebreid onderzocht hebben als de anticipatie van positieve of negatieve feedback. Neem N_t=ak_t/b dan wordt dit (a²/b)k_t(1-k_t) of dus Δk_t+1=rk_t(1-k_t). In deze vorm bepaalt de grootte van r het gedrag en simulaties maken duidelijk dat voor r groter dan 3 het gedrag chaotisch wordt. Door de inzichten van het haakformalisme kunnen we het ontstaan van dit chaotisch gedrag toewijzen aan een model waarin een entiteit en zijn intensiteit met elkaar verward worden, en dat is natuurlijk ook de reden waarom de analytische benadering niet mogelijk is (een entiteit kan niet willekeurig klein of willekeurig groot gemaakt worden). Dit is nu onze focus.

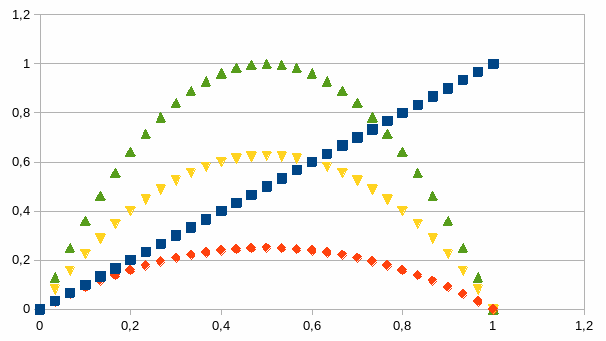
De vergelijking Δk_t+1=rk_t(1-k_t) kunnen we voorstellen met een Poincaré plot. De abscis geeft de intensiteit bij 30 stappen, dat is dus k_t, met 0<k_t<1. De ordinaat geeft de intensiteit bij de volgende stap, dat is dus k_t+Δk_t+1 en hierbij vertrekken we van een k_t=0, alhoewel we dat punt nooit kunnen bereiken. Er zijn 4 relaties weergegeven. De grafiek met vierkante punten geeft de punten waarbij geen verschil is tussen de twee intensiteiten (de “fix points” van het proces: twee opeenvolgende stappen blijken dezelfde intensiteit te hebben, Δk_t+1=0). De drie andere reeksen in de Poincaré plot geven het bestudeerde kwadratisch verband bij andere waarden van r. De ruiten geven de waarden bij r=1, de “driehoeken op de punt” geven de waarden bij r=2,5 en de “driehoeken op de zijde” geven de waarden bij r=4. De maximale waarde op de ordinaat wordt altijd bereikt bij stap 0,5 en de waarde 1 op de ordinaat wordt dus bereikt bij r=4.

Met deze toenamen kunnen we nu een volgende tabel opstellen voor positieve en negatieve feedback.

Evolutie kan alleen maar waargenomen worden als er een minimaal verschil is (k-k₀) en dat heeft dus alles te maken met de resolutie van waarnemen en dus de minimale eenheid die altijd moet verondersteld worden. Het nulpunt kunnen we nooit bereiken.

We kunnen de intensiteiten die begrensd worden in een feedback proces door twee extrema kwalitatief als volgt voorstellen:

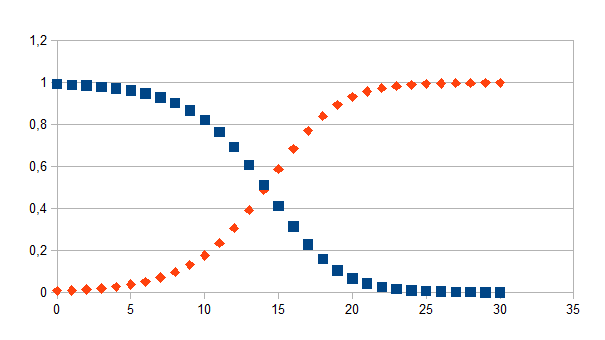
In de grafiek kiezen we voor een k₀ gelijk aan 0,005 en we tonen twee evoluties: een met vierkant punt (negatieve feedback met r=-0,4) en een met ruit punt (positieve feedback met r=0,4). De negatieve feedback start bij de minimum resolutie 0,995, de positieve feedback bij 0,005 (dat is dus de k₀). De evolutie bij 30 stappen is gegeven, voor negatieve feedback wordt 0 benaderd, voor positieve feedback wordt 1 benaderd. Hier hebben we dat verschil in beide gevallen even groot genomen (1-0,995)=(0+0,005) wat de symmetrie in de grafiek verklaart.

Door een som met een constante term kunnen we uiteraard voor de ondergrens van k een willekeurig getal kiezen in plaats van de onbereikbare 0. We kunnen ook voor de bovengrens van k een getal kiezen verschillend van 1. Immers: kies een N verschillend van nul en stel k_(t)=m_(t)N^-1. De verhouding rk_(t)(1-k_(t)) kan dan geschreven worden als rm_(t)N^-1(1-m_(t)N^-1) en dus als rm_(t)N^-2(N-m_(t)) en deze verhouding is gelijk aan nul voor m(t)=0 en ook m(t)=N. Zo genoteerd wordt de relatie de Verhulst vergelijking genoemd met twee constanten r' en K, namelijk ΔN_n+1=r'N_n(1-N_n/K). Dit maakt de volgende interpretatie duidelijk: in de beginfase is de groei van N evenredig met de grootte van N, de evenredigheid wordt gegeven door een eerste constante r' die dus een bepaalde waarde heeft van in het begin. Maar deze groei wordt beperkt doordat de tweede factor steeds kleiner wordt en uiteindelijk nul wordt wanneer de intensiteit N gelijk is aan de waarde van de tweede constante K. De constante K wordt dan “draagkracht” genoemd (van een milieu voor een bepaalde populatie) omdat dit niet anders is dan een aantal (kwantum) eenheden dat nooit kan overschreden worden. Die interpretatie kunnen we als volgt begrijpen als een negatieve feedback: hoe meer individuen er zijn in een populatie, hoe minder ruimte er is om er nog individuen aan toe te voegen, en alternatief: hoe minder individuen er zijn in een populatie, hoe meer ruimte er is om er nog individuen aan toe te voegen. Uiteraard kunnen we r'N_n(1-N_n/K) ook schrijven als r'N_n(K-N_n)/K. Volledig gelijkaardig zal ook een minimum aantal kunnen gevonden worden dat nooit zal kunnen overschreden worden in de negatieve zin (noem dit K’-N_n met K’ groter dan 0). Om dit concreet te maken kunnen we terug een voorbeeld aanhalen uit de biotische sfeer: om nieuwe eenheden te kunnen laten ontstaan zijn er typisch twee individuen nodig van verschillend geslacht. Dit is minimaal en hieruit volgt niet dat een hele populatie kan gereduceerd worden tot twee individuen van verschillend geslacht wanneer de populatie vitaal zou moeten zijn. We moeten dit alles goed begrijpen: de Verhulst vergelijking r'N_n(1-N_n/K) modelleert een aantal als gevolg van een eigenwaarde voor ofwel toename ofwel afname en de extrema worden dus nooit bereikt. Een extremum N_n=K’ of N_n=K is een verandering van eenheid van het proces en is dus een ander proces. We kunnen dat weer illustreren met een voorbeeld uit de biotische sfeer: indien de populatie zou toenemen ondanks het overschrijden van een draagkracht in een bepaald milieu, zal een nieuw proces dit kunnen modelleren: een negatieve feedback zal inzetten tot terug de draagkracht bereikt is die evenwicht kan modelleren.

Van de logistische differentievergelijking is bekend dat, als r groter dan 1 is, er een “bifurcatie” ontstaat. Wanneer r steeds groter gekozen wordt (maar kleiner dan 4) ontstaat er dan iets dat op chaos gelijkt als gevolg van zeer veel bifurcaties. We demonstreren dat in de volgende tabel voor rk_(t)(1-k_(t)), waarbij we starten bij een k(0) van 0,001. De even stappen geven een punt met ruit symbool, de oneven stappen een punt met vierkant symbool. We gebruiken ze om de “bifurcaties” te demonstreren.

Het ontstaan van chaos in het model kunnen we dus zien als het gevolg van een eigenwaarde groter dan 1, eigenwaarde die dus bij één stap ook bijkomende entiteiten creëert, eigenwaarde die niet enkel het gedrag van één entiteit modelleert (aantal dat pas na een aantal stappen kan verdubbelen).