Het meest primitieve voorbeeld van het sturen van een proces is het sturen op een verschil dat men spontaan groter of kleiner wil maken. Operationeel betekent dit dat men de beslissing neemt om datgene dat geanticipeerd werd met meer of met minder onderscheidingen te modelleren om te kunnen onderzoeken of die bijkomende onderscheidingen het verschil zouden kunnen zijn dat het verschil maakt. Wil men iets nieuw halen uit het proces (wat per definitie betekent dat het slechts achteraf kan gekend worden en dus alleen kan geanticipeerd worden) dan zal men meer en dus andere onderscheidingen nodig hebben en dus moeten divergeren. Men stuurt dan op positieve feedback. Wil men iets bestaand behouden (wat per definitie betekent dat het a priori gekend is en dus met zekerheid kan geanticipeerd worden) dan zal men proberen te vermijden dat de toestanden met andere onderscheidingen dan de reeds gebruikte beschreven moeten worden en dus zal men convergeren. Men stuurt dan op negatieve feedback.

Het resultaat is dus ordinaal meetbaar. We herkennen immers "meer" en "minder", maar niet "hoeveel meer" en "hoeveel minder" en dus vereist het meest primitieve voorbeeld niet meer dan een ordinale meting. Als men kan spreken over "hoeveel meer" en "hoeveel minder" is het relevante verschil kwantitatief meetbaar. De meting is dan de verandering van intensiteit van iets dat niet verandert en als eenheid voor de intensiteit kan gebruikt wordt en de intensiteit is dus als een accumulatie of buffer te modelleren. Soms zal men zelfs willen om de intensiteit van een aantal blijvende sporen in een medium te veranderen zoals bijvoorbeeld het aantal zandkorrels op een bepaalde plaats (en niet de soort onderscheidingen).

Bijvoorbeeld, met twee variabelen is de intensiteit 5 te definiëren als, onder zoveel andere mogelijkheden, de keuze voor een welbepaalde cirkel. De cirkel, de abstracte entiteit, treedt hierbij op als eenheid, als focus, als invariant, die van intensiteit kan veranderen. Conventioneel is de intensiteit 5 dus te definiëren als de koppels (x, y) die voldoen aan 5=x²+y². Dus de eenheid in dit voorbeeld is een cirkel c=x²+y² waarbij c verschillend is van nul en enkel de straal van de cirkel is een variabele en het verschil met c en de verhouding met c kan dan altijd berekend worden. Is c groter dan 5, dan is 5 daar een fractie van. Is c kleiner dan 5, dan is 5 daar een veelvoud van.

Operationeel kan het dus niet anders dan dat het proces gemodelleerd wordt door een wiskundig model waarin de kwantiteit in een volgende gebeurtenis niet op voorhand met zekerheid kan gekend worden, dus enkel kan geanticipeerd worden, enkel kan bepaald worden door en ten opzichte van de kwantiteit in de huidige stap. Dat is immers de essentie van feedforward met zijn noodzakelijke feedback. Hiervoor kent men twee wiskundige modellen.

1. Een eerste model noemt men circulaire processen (een variabele als functie van zichzelf modelleren) met als algemene vorm y_t+Δt=f(y_t) met y_t=g(t). Hierbij veronderstelt men f en g a priori niet gekend, maar voor een aantal functies vindt men dat het resultaat van het proces convergeert naar een "fix point". Aangezien dat punt als een attractor (dus een projector) kan geïnterpreteerd worden, kunnen we van sommige functies zeggen dat ze doelgerichtheid kunnen modelleren.

2. Een tweede model noemt men een Markov proces: men construeert een transitie matrix die de waarschijnlijkheid geeft, voor elke anticipeerbaar geachte toestand, dat deze verandert in een andere anticipeerbaar geachte toestand. Dat men niet elke transitie op voorhand kan bepalen wordt dus uitgedrukt door een waarschijnlijkheid. Aangezien een Markov proces a priori relevante en anticipeerbare toestanden veronderstelt en dat men ook een a priori waarschijnlijkheidsverdeling moet kiezen zullen we het tweede model niet volgen omdat dit niet strookt met het centraal inzicht van het haakformalisme (“niet alles kan met zekerheid gekend worden”). We hebben meer aan een Bayesiaanse waarschijnlijkheid die verschil kan maken tussen prior en posterior waarschijnlijkheden.

In het algemeen geval moet men dus uitgaan van gedeeltelijke onbekendheid van de toestand na één stap in de tijd. Ook "één stap in de tijd" is onbekend en afhankelijk van het proces zelf (en dus de elkaar uitsluitende toestanden, dus van de entiteit die als stabiel verondersteld wordt in de context van de elkaar uitsluitende toestanden van het proces). De entiteit is dus het verschil dat een verschil maakt en als eenheid gebruikt wordt, eenheid die niet verandert. Indien we elke stap in de tijd een uniek spoor geven (noem dit t), dan moeten we dus noteren dat geldt dat y_t+Δt=f(t, y_t): de functie is eveneens afhankelijk van de relevante stap.

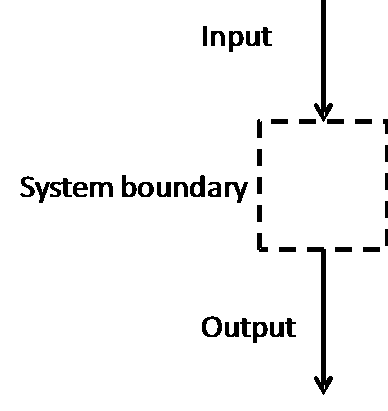
We herkennen hierin het basis diagram van een spontaan proces: y_t+Δt is de output, t en y_t zijn de input en f is de black box, de onbekende transformatie die de systeemgrens bepaalt van het spontaan proces.

Niet alles is echter onbekend: voor een bestaande entiteit (die enkel van intensiteit verandert dus) is de momentele intensiteit gekend en zal de intensiteit na één stap in de tijd niet op een onwaarneembare manier veranderd zijn omdat de entiteit als stabiel verondersteld wordt: in die ene stap in de tijd verandert de entiteit niet wat betreft zijn karakteriserende onderscheidingen en moet dus wel veranderen wat betreft onderscheidingen die de entiteit niet karakteriseren. Daarbij mogen we ook niet vergeten dat de ene stap in de tijd mee bepaald wordt door de waarnemingsmogelijkheden van het waarnemende agens-in-context. Bijvoorbeeld: de ruimtelijk positie van een entiteit karakteriseert de entiteit niet en kan variëren (de entiteit zelf verandert niet naar een andere entiteit), de grootte van de straal van een cirkel karakteriseert een cirkel niet en kan variëren (de cirkel wordt geen lijnstuk of een driedimensionaal object), het aantal zandkorrels karakteriseert een hoopje zand niet. Want, stel dat dit niet het geval zou zijn, dan zou de entiteit niet waarneembaar zijn, de verschillende onderscheidende toestanden zouden niet als toestanden van dezelfde entiteit waargenomen kunnen zijn, de entiteit zelf zou veranderd zijn en niet enkel zijn intensiteit. We schrijven niet dat de intensiteit een “kleine” stap in de tijd niet veel veranderd zal zijn: we drukken hiermee ook uit dat de verandering altijd ten opzichte van een referentie moet begrepen worden. Anders gezegd: het is onze onvermijdelijke anticipatie van wat er stabiel blijft in de tijd die de entiteit definieert die we waarnemen, het is de entiteit die we op basis van zijn karakteriserende onderscheidingen geconstrueerd hebben. Als er iets verandert dan kan het hooguit een “variabele” zijn, een aspect dat niet karakteristiek is voor de entiteit maar wel voor “zijn gedrag”, voor “de resolutie” waarmee verandering van de toestand van de entiteit kan waargenomen worden door een agens-in-context. Resoluties doen zich bijvoorbeeld voor als waargenomen verschillen die toevallig zijn en er dus niet toe doen. Resoluties geven aanleiding tot meetonzekerheid en, indien ze kwantitatief meetbaar zijn, geven ze aanleiding tot het concept van een “standaard afwijking”. Resoluties doen zich ook voor als de grootte van pixels in een foto of als de ondeelbare eenheid (en dus ook de onzekerheid) in de stap van Achilles (in de paradox van Achilles en de schildpad) enz.... Een resolutie is een verschil maar onderscheidt zich van een verschil dat een verschil maakt. Resoluties worden gegeven door het verschil tussen twee toestanden dat we als extremaal kunnen nemen (de inherente connotatie van het begrip “resolutie”) en extremaal betekent zowel ondergrens als bovengrens.

We herkennen hierin nog een ander basis diagram van een spontaan proces: de output y_t+Δt wordt “deels” terug input y_t en we hebben geen toegang tot de t van de black box, de onbekende transformatie die de systeemgrens bepaalt van het spontaan proces. We kunnen dus ook veranderingen anticiperen die binnen de systeemgrens blijven.

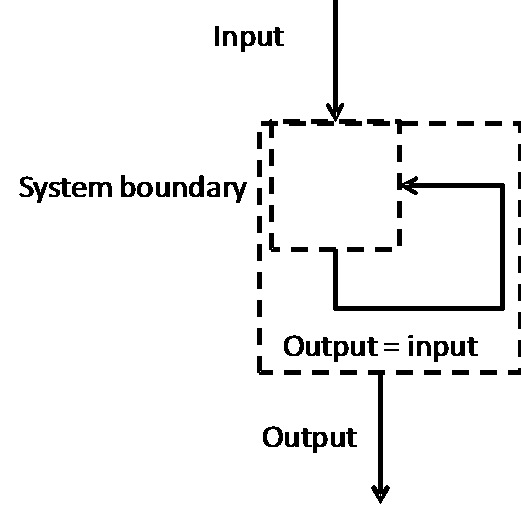
Merk op dat een transformatie soms als een pijl aangeduid wordt (zoals in de systeemdynamica) en input (en output) als een blokje aangeduid wordt (omdat een blokje meer gelijkt op een buffer).

Een verschil dat een verschil maakt, dat dus de relevante onderscheiding geeft op basis waarvan we waarnemen, stellen we voor door (x-x₀), dus als het verschil tussen een potentieel punt (namelijk x) dat nog geen waarde gekregen heeft en een geanticipeerde waarde (namelijk x₀). Met het voorbeeld van de cirkel zou (x-x₀) dus staan voor (x²+y²-5) waarbij x₀ door 5 gegeven wordt, getal dat de momentane intensiteit is van een variërende c, momentaan waargenomen en bij elke stap in het proces wellicht verschillend waargenomen. Verschillende cirkels (dus entiteiten met verschillende straal) “geanticipeerd met als referentie de cirkel met gekende straal c^1/2” kunnen dan voorgesteld worden door k(x²+y²-c) waarbij k een reëel getal is. Dus k karakteriseert de geanticipeerde resolutie van de waarneming van de cirkel met een momentaan gekende waarde en positioneert zich dus ten opzichte van c, groter of kleiner. Het is ook die k die de verandering kan kwantificeren, en dus de snelheid van het proces.

Bij positieve feedback is (x-x₀) de entiteit waarvan men vertrekt en die men wil verlaten (de entiteit is het anti-doel, het “anti-fix-point”), bij negatieve feedback is (x-x₀) de entiteit die nagestreefd wordt, en als zodanig is het “een doel”, een fix point van het model. De meeteenheid is een verschil, en dus van het type projector of "klassieke vector" en stellen we in het haakformalisme voor als de haakvector som (<>⊕h) of nog algemener als (<>⊕h₁•h₂) of (<>⊕<s•p>⊕s•q⊕r•p⊕r•q). De intensiteit k kan dus ook staan voor de intensiteit van alle entiteiten die in het haakformalisme gebruikt worden, dus bijvoorbeeld het aantal onderscheidingen dat het universum van h opspant, of ook voor het aantal niveaus van h, of het aantal atomen van h, of het aantal tussenliggende punten in een simulaneïteitsinterval enz..., met als karakteristiek dat het aantal zowel een ondergrens als een bovengrens heeft.

Het verschil tussen de anticipatie van positieve en negatieve feedback van stap t tot stap t+Δt kan dus in zijn meest eenvoudige vorm als de volgende toenames (afnames) gemodelleerd worden:

Positieve feedback: (x-x₀)_(t+Δt)=k(x-x₀)_(t)

Negatieve feedback: (x-x₀)_(t+Δt)=-k(x-x₀)_(t)

Deze modellering veronderstelt dus twee opeenvolgende toestanden (“in de tijd”, “in de ruimte”, ...), (x-x₀)_(t+Δt) en (x-x₀)_(t), dus punten die elkaar uitsluiten, die met elkaar gerelateerd zijn door hun waarneembaar verschil (dat dus afhankelijk is van waarnemer en context), wat gemodelleerd wordt door een kwantitatieve parameter k, die we ook de intensiteit van verandering of processnelheid of eigenwaarde genoemd hebben. De term (x-x₀)_(t) is wat gemeten kan worden en voldoet dus aan de definitie van een entiteit of soort. In deze context kunnen we k dan ook een variabele van een entiteit noemen die gerelateerd is aan (x-x₀), dus een aspect dat de entiteit niet karakteriseert, maar wel de stappen van de entiteit kan weergeven in een proces van verandering en dat we dus kunnen gebruiken om de verandering te anticiperen (of dus een simulatie te maken). De eenheid (x-x₀) is niet anders dan de eenheid die men veronderstelt in de analytische benadering van de differentialen. De analytische weg zullen we niet volgen maar we zullen dit wel construeren nadat het fundamenteel inzicht ontwikkeld werd waarin we eenheid en intensiteit onderscheiden.

We kunnen nu verschillende veronderstellingen maken over de factor k.

• We veronderstellen dat k de constante reële fractie is waarmee de waarde in de vorige stap van de transformatie vermenigvuldigd wordt en dus dat 0<k<1. Het is een reële metrische factor, eigen aan het spontaan proces dat in zijn meest eenvoudige vorm de constante verhouding geeft tussen twee opeenvolgende toestanden die het veranderingsproces karakteriseren van een entiteit die niet verandert, inderdaad k=(x-x₀)_(t+Δt)/(x-x₀)_(t). Dit is een vaste verhouding k die het proces karakteriseert, niet de soort die gemeten wordt. De factor tussen 0 en 1 houden wordt onderbouwd door de formele modellering van een simultaneïteitsinterval in het getallen domein. Dit drukt ook uit dat een eenheid of soort (x-x₀) altijd te normaliseren is. Als men k>1 zou veronderstellen dan zou men veronderstellen dat men eenheden kan bij creëren (en dus minstens één bijkomende onderscheiding nodig heeft) wat een bijkomende veronderstelling is (die trouwens niet gemaakt wordt in de klassieke hypothese). Inderdaad, met k=2 is wiskundig 2(x-x₀)=(x-x₀)+(x-x₀) en daar staat een plus en een plus kan enkel verantwoord worden als de twee termen van de som elkaar uitsluiten. We focusseren dus op de intensiteit van één eenheid, één aspect, één variabele. Voorbeeld: we nemen enkel de lengte van een staaf waar bij het proces van warmteopname of warmteafgifte: als de lengte van de staaf verandert in de tijd ontstaat er geen tweede staaf maar een grotere of kleinere staaf. Dit kan waargenomen worden afhankelijk van de resolutie. De verandering is onvermijdelijk een verandering tussen twee elkaar uitsluitende toestanden die daarmee intrinsiek een snelheid van verandering definiëren. De intensiteit van de eenheid "lengte van de staaf" verandert. De lengte van de staaf karakteriseert de staaf niet, het is er een aspect van. Zo'n verandering kan men enkel uitdrukken met een vermenigvuldiging. Dit is een gevolg van de veronderstelling dat er een aspect te vinden is “van de staaf” waarvan de intensiteit toeneemt of afneemt. Zuiver wiskundig gezien zou men zich kunnen voorstellen dat de lengte van een staaf verdubbelt, maar dan moet men de vraag onder ogen zien of we dat nog dezelfde staaf zouden noemen (een verdubbeling van de lengte van de staaf zonder dat zijn massa verandert zal enkel kunnen als hij dunner wordt en noemen we hem dan nog een staaf?). Elke waarneming heeft altijd een ondergrens en een bovengrens en die bepalen de eenheid. Bijvoorbeeld: een koe wordt zwaarder of lichter en hierdoor varieert haar gewicht. Het gewicht van deze concrete koe karakteriseert de koe niet. Hoewel we kunnen veronderstellen dat haar gewicht verdubbelt, toch wordt ze geen twee koeien, en dit is evenmin zo als haar gewicht halveert. Dat laatste bereiken we natuurlijk ook door ze in twee te delen maar een halve koe is geen koe meer maar een half kadaver van een koe. En dit maakt duidelijk wat gecodeerd wordt door het teken van k: is het teken van k positief, dan is de volgende stap groter dan de vorige, is het teken van k negatief, dan is de volgende stap kleiner dan de vorige.

• We kunnen veronderstellen dat k een constant complex getal is, stel k=e^2πim/n met i de wortel uit (-1) en m en n gehele getallen, dan is de n-de stap niet te onderscheiden van de eerste stap en kan men een periodiek feedback proces modelleren. Uiteraard kunnen we dat uitbreiden naar een constant quaternion en dan kunnen we de Schrödinger vergelijking modelleren.

• We kunnen veronderstellen dat k bij sommige of alle stappen verandert, k is dus een momentele intensiteit van een getalfunctie κ en drukt dan een relatie uit met de onafhankelijke variabele “tijd” of “richting in de ruimte”. De eigenwaarde k, die de resolutie van waarnemen is, is dan evenzeer afhankelijk van elkaar uitsluitende toestanden. En dus is het denkbaar dat k door een ander proces gegenereerd wordt, proces dat misschien gekarakteriseerd wordt door een k' en (deels) misschien ook afhankelijk is van de intensiteit van (x-x₀) uit het oorspronkelijk proces. Met als willekeurig voorbeeld: het zou dus kunnen dat k=k'((p-q)+r(x-x₀)_(t)+s(y-y₀)_(t))(x-x₀)_(t)

• We kunnen opmerken dat k en (x-x₀) dezelfde rol kunnen spelen.

• Meerdere verschillen die een verschil maken kunnen simultaan gemodelleerd worden. Bijvoorbeeld kunnen we twee verschillen modelleren die samen veranderen, stel (x₁-x₁₀) en (x₂-x₂₀), beide met hun eigenwaarde, respectievelijk k₁ en k₂. Hiermee wordt dan de interactie gemodelleerd van buffers waarvan de intensiteit met elkaar gerelateerd is.

Merk op dat we door deze zeer eenvoudige veronderstelling in staat zijn feedback te anticiperen en dus te simuleren wat we als anders (stel a) zouden kunnen verwachten ondanks het feit dat in werkelijkheid ook altijd iets anders zal gebeuren (stel a'). Toch doen we een stap vooruit omdat we patronen kunnen ontdekken (bijvoorbeeld periodiciteit) die in werkelijkheid ook zouden kunnen herkend worden en die ons dan minder zouden verrassen (verrassing is bijvoorbeeld meetbaar door het verschil tussen prior en posterior waarschijnlijkheid).

We kunnen nu ook verschillende veronderstellingen maken over de stappen.

De intuïtieve interpretatie van de stap t is “een stap in de tijd”. Maar dat hoeft niet. Het model dat we hanteren door het gebruik van het begrip “stap” is de uitsluiting van aspecten die we daardoor ook toestanden kunnen noemen, het is dat model dat ons in staat gesteld heeft een processnelheid te definiëren.

• Twee elkaar uitsluitende aspecten zouden ook kunnen gekarakteriseerd worden door twee elkaar uitsluitende ruimtelijke posities, waarbij de “processnelheid” dan als het verschil van een intensiteit tussen twee ruimtelijke posities (één stap) zou kunnen geïnterpreteerd worden, en de connotatie met tijd zou er dan zijn door de eigenwaarde als een weerstand te modelleren die moet overwonnen worden om van de ene positie naar de andere te gaan. We hebben hier het begrip diffusie (versus convectie) van een invariante massa in een medium voor. We kunnen dus evenzeer noteren dat:

Positieve feedback: (x-x₀)_(s+Δs)=k(x-x₀)_(s) met 0<k<1

Negatieve feedback: (x-x₀)_(s+Δs)=-k(x-x₀)_(s) met 0<k<1

Dit is uiteraard hetzelfde patroon.

• Twee elkaar uitsluitende aspecten zouden ook kunnen gekarakteriseerd worden door twee elkaar uitsluitende energetische niveaus, waarbij de processnelheid dan als de overgang van een intensiteit tussen twee energetische niveaus (één stap) zou kunnen geïnterpreteerd worden, los van enige connotatie met tijd (denk aan de absorptie en emissie van een foton). We gebruiken dan het begrip dissipatie versus concentratie van energie, zowel in ruimte als in tijd. We kunnen dus evenzeer noteren dat:

Positieve feedback: (x-x₀)_(e+Δe)=k(x-x₀)_(e) met 0<k<1

Negatieve feedback: (x-x₀)_(e+Δe)=-k(x-x₀)_(e) met 0<k<1

Dit is uiteraard hetzelfde patroon.