Nu we de stelling van Bayes als techniek begrepen hebben kunnen we uitleggen hoe de getallen die bekomen worden uitgaande van effectieve experimenten kunnen gebruikt worden om de potentiële tralie van de werkelijkheid te construeren, want uiteindelijk gaat het daarom: de voorspellende waarde van relevante experimenten.

In een tralie kunnen ook andere punten elkaar uitsluiten dan de AND-atomen van dat universum. Dit geldt ook in een gecollapst universum. Sommige atomen of elkaar uitsluitende punten die zich nog van elkaar onderscheiden voor de collaps zullen zich niet meer onderscheiden na de collaps en zullen punten worden die zich op een andere diepte in de tralie bevinden dan de atoomdiepte of de oorspronkelijke diepte.

Dat “elkaar uitsluiten” afhankelijk is van een soort collaps is in het haakformalisme heel nauwkeurig uit te drukken: een punt dat andere punten uitsluit, een <<A>_i> moet eigenlijk geschreven worden als een <<A>_i>/A₀, namelijk onder de voorwaarde A₀, wat we een uitsluitingsniveau genoemd hebben. De meest primitieve context die we in het haakformalisme onderscheiden, namelijk <>, doet zich in de Bayesiaanse waarschijnlijkheid voor als de onvermijdelijke voorwaarde A₀.

Dus dan wordt de stelling van Bayes

P(<<A>_i>/(E_j/A₀)={P(E_j/(<<A>_i>/A₀))P(<<A>_i>/A₀)}{Σ_iP(E_j/(<<A>_i>/A₀))P(<<A>_i>/A₀)}^-1

We kunnen nu twee getallen ten opzichte van een derde getal onderscheiden:

P(<<A>_i>/(E_j/A₀)=κP(<<A>_i>/A₀) met

κ={P(E_j/(<<A>_i>/A₀))}{Σ_jP(E_j/(<<A>_i>/A₀))P(<<A>_i>/A₀)}^-1

We merken op dat altijd 1<κ zal gelden als <<A>_i> door de collaps die P(E_j)=1 maakt niet irrelevant geworden is. Dit maakt dan de volgende interpretatie mogelijk: de stelling van Bayes veronderstelt een dynamiek als volgt:

P(<<A>_i>/A₀) wordt de “prior” kans genoemd, dus de kans van het waarnemen van <<A>_i> gegeven A₀ “vooraleer” een nieuwe collaps E_j waargenomen is. Dit is dus de “oorspronkelijke” verwachting voor <<A>_i>, de waarschijnlijkheid dat <<A>_i> gebeurt simultaan met A₀ en dus voor een nieuwe waarneming uitgevoerd werd. Dat is dus wat geanticipeerd wordt en de reden om een doelgericht proces te starten. Bijvoorbeeld: als elke <<A>_i> een andere <<A>_i> uitsluit en er zijn n punten <<A>_i> mogelijk, dan is de verwachting dat “een bepaalde <<A>_i> waargenomen is” als “A₀ waargenomen is” gelijk aan 1/n. Dit maakt duidelijk dat elke <<A>_i> door dezelfde onderscheidingen moet opgebouwd zijn (anders kan “elkaar uitsluiten” niet operationeel gedefinieerd worden). Dat betekent niet dat elke <<A>_i> ervaren moet kunnen worden, immers wanneer elke <<A>_i> ervaringswaarde <<>> heeft dan sluiten ze elkaar uit. De <<A>_i> zijn de elementen van de resultatenruimte Ω, elke <<A>_i> is “gebeurbaar” binnen de resultatenruimte.

P(<<A>_i>/(E_j/A₀) wordt de “posterior” kans genoemd, dus de kans van het waarnemen van <<A>_i> gegeven E_j, dus wanneer E_j waargenomen is, “na” de nieuwe collaps dus. Dit is dus de nieuwe verwachting voor <<A>_i>, de waarschijnlijkheid dat <<A>_i> simultaan met A₀ waargenomen wordt. Bijvoorbeeld: E_j kan onmogelijk simultaan met een aantal <<A>_i> optreden, dus wanneer men E_j waarneemt moeten die mogelijkheden die a priori verondersteld werden niet meer meegerekend worden. Met het voorbeeld dat de waarschijnlijkheid dat “een bepaalde <<A>_i> waargenomen is”, gelijk is aan 1/n, wordt n dus kleiner en dus de waarschijnlijkheid groter.

P(E_j/(<<A>_i>/A₀)) is de verwachting van E_j indien <<A>_i>/A₀ gegeven is (een gecollapste tralie waarbij A₀ ervaren is, met elkaar uitsluitende punten <<A>_i>) die overeenkomt met de waarschijnlijkheid dat E_j simultaan met <<A>_i> waargenomen wordt in die gecollapste tralie, waar dus enkel maar die <<A>_i> overblijven. Hoe verder de metrische afstand (niveauverschil) van E_j tot de punten <<A>_i> in de tralie van potentiële punten, hoe groter de verwachting om bij het momentaan realiseren van een van die punten ook die E_j te realiseren.

We kunnen de stelling van Bayes dus gebruiken wanneer we P(E_j/(<<A>_i>/A₀)) kunnen opbouwen. We moeten dan beschikken over al de relevante elkaar uitsluitende punten in een potentiële tralie en we moeten kunnen kiezen die “een na een” (elkaar uitsluitend) te laten gebeuren in de context A₀. Dit kunnen we afleiden van de verschillende sporen die ontstaan en afgescheiden worden, dus niet ingebouwd worden in de tralie. Een andere mogelijk is er niet, aangezien we veronderstellen dat de elkaar uitsluitende punten niet te kiezen zijn en enkel kunnen gebeuren, we moeten dus voldoende kunnen proberen zonder zekerheid te hebben dat we alle mogelijke gebeurtenissen en dus sporen zouden kunnen waarnemen. Tijdens al die realisaties moeten we de waarneming E_j uitvoeren en categoriseren in twee categorieën: E_j treedt op ofwel E_j treedt niet op. Dit kunnen we uitvoeren voor alle E_j die ons interesseren. De E_j moeten elkaar uitsluiten. Dit is gemakkelijk te realiseren door waarnemingen in de tijd uit te voeren, dit is juist de generieke eigenschap van “tijd”.

Wanneer we dan later een E_j waarnemen dan laat de stelling van Bayes toe om te berekenen wat de waarschijnlijkheid is dat E_j met een van die mogelijke elkaar uitsluitende punten <<A>_i> simultaan waargenomen werd. We kiezen daarvoor een context die we voor alle testen als onveranderd veronderstellen (namelijk A₀), en kiezen voor het waarnemen van een E_j. Dit zal dan gebeuren als een complexe mogelijkheid (een disjunctie van niet te kiezen atomen) <<A>_i>_j die we dan zo goed mogelijk beschrijven. Die beschrijving proberen we terug te realiseren als we de test willen herhalen, want de hele waarschijnlijkheidsrekening staat of valt met de mogelijkheid om entiteiten te onderscheiden, dus met de mogelijkheid tot herhaalbaarheid (in dit geval namelijk van A₀). Deze procedure is dan ook repetitief herhaalbaar waarbij men goed moet beseffen dat het onvermijdelijk is dat men vertrekt van een A₀ die staat voor de grens van het ervaren door een bepaald agens en dat de waarneming mogelijk is door sporen die moeten ontstaan en niet te kiezen zijn. A₀ en de sporen kunnen extreem ingewikkeld zijn voor een andere agens (die A_p als grens zou hebben en andere sporen waarneemt), maar voor het agens met A₀ als grens is die ingewikkeldheid irrelevant.

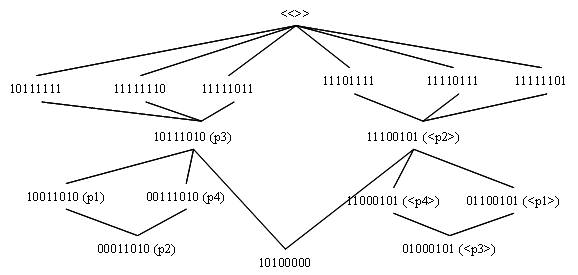
We illustreren de verschillende waarnemingen met steeds hetzelfde voorbeeld zodanig dat vergelijking mogelijk wordt en dat in de onderstaande deeltralie voorgesteld wordt, deeltralie waarin we p3 versus <p2> niet onderscheiden van M versus M^<> en waarin 10100000 de rol inneemt van de M•M^<>↔MM^<>.

In de onderstaande tabel zijn de 8 AND-atomen van het drie-onderscheidingen universum weergegeven. Dat zijn de <<A>_i> als de elementen van de resultatenruimte Ω, waarbij elke <<A>_i> een conjunctie is van de onderscheidingen a, b, c of hun inbedding. De eerste kolom geeft een naam aan elk atoom (we gebruiken daarvoor de T van Toestand), de tweede kolom geeft het haakbit model. De derde kolom geeft het haakbit model in de veronderstelling dat 10100000 niet kan onderscheiden worden van 00000000, waarmee we een A₀ modelleren in een gecollapste tralie. Merk op dat T₆ en T₈ dan niet meer van elkaar te onderscheiden zijn. De vierde kolom geeft een naam aan twee elkaar uitsluitende gebeurtenissen, de punten E₁ en E₂ en geeft het nieuw supremum de naam E₃ (namelijk de T₆ en T₈ die niet meer van elkaar te onderscheiden zijn). De laatste kolom geeft een naam aan drie elkaar uitsluitende punten E₂, E₄ en E₅ met hetzelfde supremum E₃. Beide laatste kolommen geven twee verschillende experiment opstellingen waarin enkel de gebeurtenissen E₂ en E₃ gemeenschappelijk waargenomen worden. Merk op dat E₃ enkel kan gebeuren en niet kan gekozen worden. In de ene opstelling kan bijkomend slechts E₁ waargenomen worden, in de andere opstelling kan bijkomend ofwel E₄, ofwel E₅ waargenomen worden. De tabel geeft de opbouw van de P(E_j/(<<A>_i>/A₀)).

De waarschijnlijkheden in die twee verschillende waarneming contexten zijn:

1=P(A₀)=P(E₁)+P(E₂)=3/6+3/6=6/6

1=P(A₀)=P(E₂)+P(E₄)+P(E₅)=3/6+1/6+2/6=6/6

We kunnen nu eens de waarschijnlijkheid berekenen met de Bayes formule voor het geval E₅ waargenomen werd:

P(<<A>_i>/(E/A₀)={P(E/(<<A>_i>/A₀))P(<<A>_i>/A₀)}{Σ_iP(E/(<<A>_i>/A₀))P(<<A>_i>/A₀)}^-1 of dus

(2/6*1/6)*((3/6+1/6+2/6)*1/6)^-1=2/6

Met deze tabel illustreren we dus dat het denkbaar is dat het aantal waarneming contexten kan aangepast worden naarmate we meer elkaar uitsluitende gebeurtenissen kunnen bedenken, waarmee we dus steeds meer een één-op-één afbeelding met de uiterste elkaar uitsluitende punten in de gecollapste tralie met infimum A₀ benaderen. In de tralie met infimum <> zijn die elkaar uitsluitende punten dan de AND-atomen T_i.

Het is dan ook duidelijk dat de huidige stand van kennis over een tralie kan beschreven worden door een lijst van nodes waaraan telkens een bepaalde voorwaardelijke waarschijnlijkheid toegekend is.