Zoals de
complexe en perplexe getallen uit het 1-splitsing universum
kunnen afgeleid worden, kunnen de quaternionen afgeleid worden uit
het 2-splitsing universum.
Conventioneel is er nogal wat verwarring hoe een quaternion
voorgesteld wordt als een 4x4 matrix. Dit heeft natuurlijk alles te
maken met de signaturen die willekeurig kunnen gekozen worden als men
de eenheden beschouwt als te vermenigvuldigen met een scalair met een
willekeurig teken. Het enige dat men dan nog als patroon van
signaturen moet onder ogen zien is de symmetrie van tegengestelde
signaturen ten opzichte van de diagonalen. Die diagonalen nemen
immers een speciale plaats in in het matrixproduct. Dank zij het
onderzoek naar de operatoren in het 2-splitsing universum kunnen
we de conventies beter plaatsen.
Er zijn twee veel voorkomende voorstelling voor een willekeurig
quaternion:
de operator
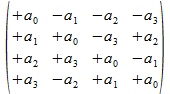 volgens
de normale regels van Hamilton, wat we nu in de vertaling met de
inzichten van het haakformalisme kunnen schrijven als
a0•1-a1•k-a2•j-a3•i,
waarbij 1-k-j-i als signatuurmatrix overeenkomt met de bitstring
(---+)
volgens
de normale regels van Hamilton, wat we nu in de vertaling met de
inzichten van het haakformalisme kunnen schrijven als
a0•1-a1•k-a2•j-a3•i,
waarbij 1-k-j-i als signatuurmatrix overeenkomt met de bitstring
(---+)
de operator
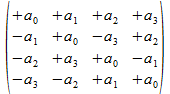 volgens
de reverse regels van Hamilton, wat we nu in de vertaling met de
inzichten van het haakformalisme kunnen schrijven als
a0•1+a1•k+a2•j+a3•i
en waarbij 1+k+j+i als signatuurmatrix overeenkomt met de
bitstring (xxx+).
volgens
de reverse regels van Hamilton, wat we nu in de vertaling met de
inzichten van het haakformalisme kunnen schrijven als
a0•1+a1•k+a2•j+a3•i
en waarbij 1+k+j+i als signatuurmatrix overeenkomt met de
bitstring (xxx+).
Dit zijn maar twee van de 16 mogelijke atomen (potentiële of
gecollapste) van het twee onderscheidingen universum, en er wordt een
andere keuze gemaakt uit de twee gesloten sets die zouden gebruikt
kunnen worden. Rekening houdend met de naamgeving van de basis die in
elkaar kan gepermuteerd worden zijn er dus maar twee van de 48
mogelijke overeenkomsten van 3 namen en signatuurmatrices in gebruik
(beide sets hebben de basis 1 als gemeenschappelijke component).
Hiermee hebben we dus de vooronderstellingen van de quaternionen in
het haakformalisme afgeleid. Hiermee is ook duidelijk dat zowel de
onderscheidende als verenigende kracht van het haakformalisme veel
dieper gaat.
De vermenigvuldigingstabel voor quaternionen is als volgt:
|
•
|
1
|
-1
|
i
|
-i
|
j
|
-j
|
k
|
-k
|
|
1
|
1
|
-1
|
i
|
-i
|
j
|
-j
|
k
|
-k
|
|
-1
|
-1
|
1
|
-i
|
i
|
-j
|
j
|
-k
|
k
|
|
i
|
i
|
-i
|
-1
|
1
|
k
|
-k
|
-j
|
j
|
|
-i
|
-i
|
i
|
1
|
-1
|
-k
|
k
|
j
|
-j
|
|
j
|
j
|
-j
|
-k
|
k
|
-1
|
1
|
i
|
-i
|
|
-j
|
-j
|
j
|
k
|
-k
|
1
|
-1
|
-i
|
i
|
|
k
|
k
|
-k
|
j
|
-j
|
-i
|
i
|
-1
|
1
|
|
-k
|
-k
|
k
|
-j
|
j
|
i
|
-i
|
1
|
-1
|
Het element 1 is van orde 1.
Het element -1 is van orde 2.
De elementen +i, -i, +j, -j, +k, -k zijn van orde 4.
De quaternionen vormen een groep, een van de vijf mogelijke
groepen van orde 8.
De quaternion groep heeft vijf subgroepen die dus ook in het
haakformalisme kunnen gedefinieerd worden in functie van de
basisvectoren van het twee onderscheidingen universum: (1); (1, -1);
(1, -1, i, -i); (1, -1, j, -j); (1, -1, k, -k) die we bijvoorbeeld
kunnen afbeelden op (<<>>); (<<>>, <>);
(<<>>, <>, <a>, a); (<<>>, <>,
<b>, b); (<<>>, <>, a•b, <a•b>).
Deze herkennen we natuurlijk als de vijf twee-dimensionele basissen
waarin een willekeurige welgevormde haakuitdrukking kan geschreven
worden:
H=H•(<<>>)=H•(<>⊕<>)⊕H•(<>⊕<<>>)
H=<<>>•(<>⊕<H>)⊕<>•(<>⊕H)
H=<q•r>•(<>⊕p•q)⊕p•s•(<>⊕<p•q>)
H=<q•r>•(<>⊕r•s)⊕p•s•(<>⊕<r•s>)
H=<q•r>•(<>⊕p•q•r•s)⊕p•r•(<>⊕<p•q•r•s>)
De acties die in het 2-splitsing universum gedefinieerd werden
maken duidelijk wat de veronderstellingen zijn die aanleiding geven
tot de quaternionen. De veronderstelling is dat de haakvectoren hi
niet verschillend zijn van elkaar en een welbepaalde getalwaarde
hebben. Bijvoorbeeld: 1(+h1, +h2, +h3,
+h4)=(+h1, +h2, +h3, +h4)
en hierin hebben de hi de getalwaarde a0. Met
een ander voorbeeld: k(+h1, +h2, +h3,
+h4)=(-h4, +h3, -h2, +h1)
en hierin hebben de hi de waarde a2. Dit maakt
duidelijk dat er ook conventioneel een uitbreiding zal gezocht worden
voor de quaternionen om diepere structuren te kunnen voorstellen met
behulp van getalwaarden. Een voor de hand liggende keuze is om
complexe getallen te gebruiken als coëfficiënten, en de hi
dus de getalwaarde van een complex getal te geven. Uiteraard zal men
de hi ook de getalwaarde van een quaternion kunnen geven.
Dieper moet men niet gaan om elkaar uitsluitende punten
(gebeurtenissen) weer te geven aangezien we bewezen hebben dat alle
welgevormde haakuitdrukkingen als een som van vier componenten
(standpunten) kunnen voorgesteld worden en
hiermee tralies (met elkaar uitsluitende punten) kunnen geconstrueerd
worden.
Merk op dat de veronderstellingen van een getalwaarde niet moeten
gemaakt worden in het haakformalisme: de hi moeten geen
waarde hebben, ze kunnen perfect potentiële structuren zijn,
waarmee ze dus veralgemeningen zijn van gelijk welke functie of
“indien...dan” constructie.
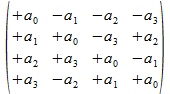 volgens
de normale regels van Hamilton, wat we nu in de vertaling met de
inzichten van het haakformalisme kunnen schrijven als
a0•1-a1•k-a2•j-a3•i,
waarbij 1-k-j-i als signatuurmatrix overeenkomt met de bitstring
(---+)
volgens
de normale regels van Hamilton, wat we nu in de vertaling met de
inzichten van het haakformalisme kunnen schrijven als
a0•1-a1•k-a2•j-a3•i,
waarbij 1-k-j-i als signatuurmatrix overeenkomt met de bitstring
(---+)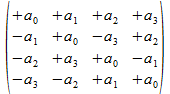 volgens
de reverse regels van Hamilton, wat we nu in de vertaling met de
inzichten van het haakformalisme kunnen schrijven als
a0•1+a1•k+a2•j+a3•i
en waarbij 1+k+j+i als signatuurmatrix overeenkomt met de
bitstring (xxx+).
volgens
de reverse regels van Hamilton, wat we nu in de vertaling met de
inzichten van het haakformalisme kunnen schrijven als
a0•1+a1•k+a2•j+a3•i
en waarbij 1+k+j+i als signatuurmatrix overeenkomt met de
bitstring (xxx+).