⊗
![]()
![]()
![]()
![]()
![]()
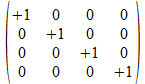
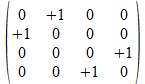
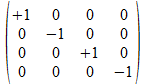
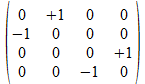
![]()
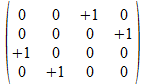
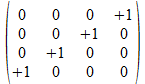
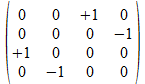

![]()
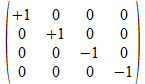
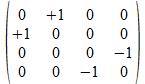
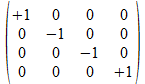
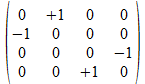
![]()

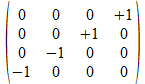
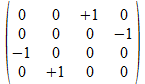
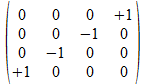
Op basis van de vier 2x2 “positieve operatoren” kunnen met het Kronecker product de zestien mogelijke positieve 4x4 operatoren opgebouwd worden. Met de inbedding van de operatoren krijgen we dan 32 operatoren. Dit zal leiden tot nieuwe patronen die in samenwerking met Donald Leenknegt ontdekt werden in de gesloten structuren die 4x4 operatoren kunnen vormen door de operator vermenigvuldiging (of matrix product). Dit leidt dan tot een dieper inzicht in “de regels van Hamilton” voor vermenigvuldiging van quaternionen.
In de eerste tabel geven we de 16 bewerkingen:
|
⊗ |
ε |
υ |
ν |
νυ |
|
ε |
ε⊗ε |
ε⊗υ |
ε⊗ν |
ε⊗νυ |
|
υ |
υ⊗ε |
υ⊗υ |
υ⊗ν |
υ⊗νυ |
|
ν |
ν⊗ε |
ν⊗υ |
ν⊗ν |
ν⊗νυ |
|
νυ |
νυ⊗ε |
νυ⊗υ |
νυ⊗ν |
νυ⊗νυ |
Dit vertalen we nu in 4x4 operatoren
|
⊗ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
De kleur in de tabel wordt verder verduidelijkt.
We gaan nu de kwadraten berekenen van de operatoren.
|
⊗2 |
ε |
υ |
ν |
νυ |
|
ε |
+ε |
+ε |
+ε |
-ε |
|
υ |
+ε |
+ε |
+ε |
-ε |
|
ν |
+ε |
+ε |
+ε |
-ε |
|
νυ |
-ε |
-ε |
-ε |
+ε |
We merken dat de eenheidsoperator ε een unieke plaats inneemt en dus deel zal moeten uitmaken van alle ruimten die met deze operatoren kunnen opgespannen worden met behulp van het matrixproduct. We merken op dat 10 kwadraten tot de positieve operatoren behoren en 6 tot de negatieve operatoren.
We merken op dat de operatoren in een niet gekleurde achtergrond eerder met de linksboven/rechtsonder diagonaal gerelateerd zijn en dat de operatoren in een blauwe achtergrond eerder met de linksonder/rechtsboven diagonaal gerelateerd zijn. We kiezen voor de richting gegeven door de langste opeenvolging van symbolen (4 op de hoofddiagonaal en 3 op de nevendiagonaal).
Als patroon vinden we voor de niet gekleurde achtergrond
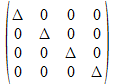 of
of
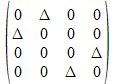
Als patroon vinden we voor de blauwe achtergrond
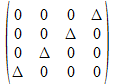 of
of
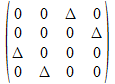
We zullen telkens een vertegenwoordiger van deze vier patronen nodig hebben om alle 16 cellen van een 4x4 operator te voorzien van een betekende bit. Dus dit beperkt al de mogelijke koppels tot deze die gegeven worden in de onderstaande tabellen. In de tabellen zijn de operatoren onderlijnd die als kwadraat de negatieve ε operator hebben.
|
|
|
|
ε ⊗ ε |
ε ⊗ υ |
|
ε ⊗ ε |
ε ⊗ νυ |
|
ε ⊗ ε |
ν ⊗ υ |
|
ε ⊗ ε |
ν ⊗ νυ |
|
|
|
|
ε ⊗ ν |
ε ⊗ υ |
|
ε ⊗ ν |
ε ⊗ νυ |
|
ε ⊗ ν |
ν ⊗ υ |
|
ε ⊗ ν |
ν ⊗ νυ |
|
|
|
|
ν ⊗ ε |
ε ⊗ υ |
|
ν ⊗ ε |
ε ⊗ νυ |
|
ν ⊗ ε |
ν ⊗ υ |
|
ν ⊗ ε |
ν ⊗ νυ |
|
|
|
|
ν ⊗ ν |
ε ⊗ υ |
|
ν ⊗ ν |
ε ⊗ νυ |
|
ν ⊗ ν |
ν ⊗ υ |
|
ν ⊗ ν |
ν ⊗ νυ |
|
|
|
|
υ ⊗ υ |
υ ⊗ ε |
|
υ ⊗ υ |
υ ⊗ ν |
|
υ ⊗ υ |
νυ ⊗ ε |
|
υ ⊗ υ |
νυ ⊗ ν |
|
|
|
|
υ ⊗ νυ |
υ ⊗ ε |
|
υ ⊗ νυ |
υ ⊗ ν |
|
υ ⊗ νυ |
νυ ⊗ ε |
|
υ ⊗ νυ |
νυ ⊗ ν |
|
|
|
|
νυ ⊗ υ |
υ ⊗ ε |
|
νυ ⊗ υ |
υ ⊗ ν |
|
νυ ⊗ υ |
νυ ⊗ ε |
|
νυ ⊗ υ |
νυ ⊗ ν |
|
|
|
|
νυ ⊗ νυ |
υ ⊗ ε |
|
νυ ⊗ νυ |
υ ⊗ ν |
|
νυ ⊗ νυ |
νυ ⊗ ε |
|
νυ ⊗ νυ |
νυ ⊗ ν |
We kunnen nu de volgende voorwaarden stellen voor de constructie van een gesloten ruimte met vier opbouwende operatoren:
de eenheidsoperator ε is een van de vier operatoren
van de twee patronen is er telkens één vertegenwoordiger, waarbij er dus maar 3 mogelijkheden overblijven omdat ε reeds een plaats inneemt
er zijn twee mogelijkheden van combinaties in een 1&3 patroon: een operator met positief kwadraat versus drie operatoren met negatief kwadraat ofwel een operator met negatief kwadraat versus drie operatoren met positief kwadraat. Dit wordt gemotiveerd door het algemeen 1&3 patroon (of creatief product patroon) van welgevormde haakuitdrukkingen
het matrixproduct moet gesloten zijn voor de ruimte, dus met ei een operator, moet het matrixproduct eiej tot de ruimte behoren
We kunnen nu alle (en de enige) mogelijkheden construeren die overblijven. We doen dat in twee groepen.
|
ε ⊗ ε |
ε ⊗ νυ |
νυ ⊗ ε |
υ ⊗ νυ |
|
ε ⊗ ε |
ε ⊗ νυ |
νυ ⊗ ν |
υ ⊗ νυ |
|
ε ⊗ ε |
ε ⊗ νυ |
νυ ⊗ ε |
νυ ⊗ υ |
|
ε ⊗ ε |
ε ⊗ νυ |
νυ ⊗ ν |
νυ ⊗ υ |
|
ε ⊗ ε |
ν ⊗ νυ |
νυ ⊗ ε |
υ ⊗ νυ |
|
ε ⊗ ε |
ν ⊗ νυ |
νυ ⊗ ν |
υ ⊗ νυ |
|
ε ⊗ ε |
ν ⊗ νυ |
νυ ⊗ ε |
νυ ⊗ υ |
|
ε ⊗ ε |
ν ⊗ νυ |
νυ ⊗ ν |
νυ ⊗ υ |
Controle op de geslotenheid van het matrixproduct reduceert deze tabel tot twee mogelijkheden, en we klasseren deze operatoren nu ook in de categorieën die gebruikt worden voor een quaternion
|
1 |
i |
j |
k |
|
|
ε ⊗ ε |
ε ⊗ νυ |
νυ ⊗ ν |
νυ ⊗ υ |
(1) |
|
ε ⊗ ε |
ν ⊗ νυ |
νυ ⊗ ε |
υ ⊗ νυ |
(2) |
De vier eerste operatoren voldoen aan “de normale regels van Hamilton”, namelijk ij = k; jk = i; ki = j en ji = -k; kj = -i; ik = -j
De vier laatste voldoen aan “de reverse regels van Hamilton”, namelijk ij = -k; jk = -i; ki = -j en ji = k; kj = i; ik = j
In 4x4 operator levert dit de volgende tabel:
|
1 |
i |
j |
k |
|
|
|
|
|
|
(1) |
|
|
|
|
|
(2) |
|
ε ⊗ ε |
ε ⊗ υ |
υ ⊗ υ |
νυ ⊗ ε |
|
ε ⊗ ε |
ε ⊗ υ |
υ ⊗ υ |
νυ ⊗ ν |
|
ε ⊗ ε |
ε ⊗ υ |
υ ⊗ νυ |
υ ⊗ ε |
|
ε ⊗ ε |
ε ⊗ υ |
υ ⊗ νυ |
υ ⊗ ν |
|
ε ⊗ ε |
ε ⊗ υ |
νυ ⊗ υ |
υ ⊗ ε |
|
ε ⊗ ε |
ε ⊗ υ |
νυ ⊗ υ |
υ ⊗ ν |
|
ε ⊗ ε |
ε ⊗ υ |
νυ ⊗ νυ |
νυ ⊗ ε |
|
ε ⊗ ε |
ε ⊗ υ |
νυ ⊗ νυ |
νυ ⊗ ν |
|
ε ⊗ ε |
ε ⊗ νυ |
υ ⊗ υ |
υ ⊗ ε |
|
ε ⊗ ε |
ε ⊗ νυ |
υ ⊗ υ |
υ ⊗ ν |
|
ε ⊗ ε |
ε ⊗ νυ |
νυ ⊗ νυ |
υ ⊗ ε |
|
ε ⊗ ε |
ε ⊗ νυ |
νυ ⊗ νυ |
υ ⊗ ν |
|
ε ⊗ ε |
ν ⊗ υ |
υ ⊗ υ |
νυ ⊗ ε |
|
ε ⊗ ε |
ν ⊗ υ |
υ ⊗ υ |
νυ ⊗ ν |
|
ε ⊗ ε |
ν ⊗ υ |
υ ⊗ νυ |
υ ⊗ ε |
|
ε ⊗ ε |
ν ⊗ υ |
υ ⊗ νυ |
υ ⊗ ν |
|
ε ⊗ ε |
ν ⊗ υ |
νυ ⊗ υ |
υ ⊗ ε |
|
ε ⊗ ε |
ν ⊗ υ |
νυ ⊗ υ |
υ ⊗ ν |
|
ε ⊗ ε |
ν ⊗ υ |
νυ ⊗ νυ |
νυ ⊗ ε |
|
ε ⊗ ε |
ν ⊗ υ |
νυ ⊗ νυ |
νυ ⊗ ν |
|
ε ⊗ ε |
ν ⊗ νυ |
υ ⊗ υ |
υ ⊗ ε |
|
ε ⊗ ε |
ν ⊗ νυ |
υ ⊗ υ |
υ ⊗ ν |
|
ε ⊗ ε |
ν ⊗ νυ |
νυ ⊗ νυ |
υ ⊗ ε |
|
ε ⊗ ε |
ν ⊗ νυ |
νυ ⊗ νυ |
υ ⊗ ν |
Controle op de geslotenheid van het matrixproduct reduceert deze tabel tot zes mogelijkheden:
|
1 |
i |
j |
k |
|
|
ε ⊗ ε |
ε ⊗ υ |
νυ ⊗ ε |
υ ⊗ υ |
(1) |
|
ε ⊗ ε |
ε ⊗ υ |
υ ⊗ ε |
υ ⊗ νυ |
(2) |
|
ε ⊗ ε |
ν ⊗ νυ |
υ ⊗ ε |
υ ⊗ υ |
(3) |
|
ε ⊗ ε |
ε ⊗ νυ |
υ ⊗ ν |
νυ ⊗ νυ |
(4) |
|
ε ⊗ ε |
ν ⊗ υ |
υ ⊗ ν |
νυ ⊗ υ |
(5) |
|
ε ⊗ ε |
ν ⊗ υ |
νυ ⊗ ν |
νυ ⊗ νυ |
(6) |
Deze zes mogelijkheden kunnen we nu specifieker onderzoeken en splitsen we nu op in twee groepen
Drie voldoen aan de normale regels van Hamilton, namelijk ij = k; jk = i; ki = j en ji = -k; kj = -i; ik = -j:
|
1 |
i |
j |
k |
|
|
|
|
|
|
(1) |
|
|
|
|
|
(2) |
|
|
|
|
|
(3) |
Drie voldoen aan de reverse regels van Hamilton, namelijk ij = -k; jk = -i; ki = -j en ji = k; kj = i; ik = j
|
1 |
i |
j |
k |
|
|
|
|
|
|
(4) |
|
|
|
|
|
(5) |
|
|
|
|
|
(6) |
We verzamelen nu de operatoren groepen in twee categorieën: de “normaal Hamilton” en de “reverse Hamilton”. Merk op dat binnen deze categorieën er ook een 1&3 opsplitsing te onderscheiden is gegeven door de operatoren die als kwadraat de negatieve identiteitsmatrix hebben (eerste rij) en de operatoren die als kwadraat de positieve identiteitsmatrix hebben (drie volgende rijen).
|
1 |
i |
j |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
i |
j |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
We kunnen nu het verband leggen met de vorm van de operator als een herschikking van een lijst:
De eerste rij van de operatoren volgens het normaal Hamilton verband komt overeen met de operatoren set (1, p, q, r) als (1, i, k, j).
De eerste rij van de operatoren volgens het reverse Hamilton verband komt overeen met de operatoren set (1, e, f, g) als (1, -j, -k, -i).
De constructie van alle 4x4 “positieve operatoren” die gesloten ruimtes vormen toont duidelijk dat er 8 verschillende gesloten ruimtes mogelijk zijn. Deze ruimtes hebben hun negatieve tegenpool, zodanig dat er op het eerste zicht 16 verschillende gesloten ruimtes geconstrueerd kunnen worden met 4x4 operatoren. Maar dat is een veel te snelle conclusie aangezien de positieve en negatieve operatoren onderling nog relaties hebben tot elkaar. Die relaties zijn een gevolg van de niet-commutativiteit van het matrix product van de i, j en k operatoren: verwisselt men immers twee operatoren dan wordt de negatieve vorm van de operator gegenereerd door het matrix product.
Deze relaties die de mogelijke permutaties beschrijven worden bondig weergegeven door de volgende regels:
men mag twee willekeurig operatoren van teken wisselen
men mag één operator van teken wisselen en er tegelijk twee onderling omwisselen
men mag drie operatoren van teken wisselen en er tegelijk twee onderling omwisselen.
Deze relaties werden natuurlijk al opgemerkt voor de quaternionen en ze leiden tot 2x24 mogelijke varianten, 24 die voldoen aan de normale regels van Hamilton, 24 die voldoen aan de reverse regels van Hamilton. Zij geven aanleiding tot twee groepen van gesloten ruimtes die elk door16 operatoren operatoren opgespannen worden die verschillend zijn, behalve de positieve identiteitsoperator. Dit zijn dus 32 operatoren met een positieve identiteitsoperator. Een volledig analoge constructie is mogelijk met een negatieve identiteitsoperator, zodanig dat er in totaal 64 gesloten ruimtes mogelijk zijn.
Lijst van de permutaties die voldoen aan de normale regels van Hamilton
|
(+i)(+j)(+k) |
(+j)(+k)(+i) |
(+k)(+i)(+j) |
(-i)(-j)(+k) |
(-j)(+k)(-i) |
(+k)(-i)(-j) |
|
(+j)(-i)(+k) |
(+k)(-j)(+i) |
(+k)(+j)(-i) |
(-i)(+k)(+j) |
(-j)(+i)(+k) |
(+i)(+k)(-j) |
|
(+i)(-j)(-k) |
(-j)(-k)(+i) |
(-k)(+i)(-j) |
(-i)(+j)(-k) |
(+j)(-k)(-i) |
(-k)(-i)(+j) |
|
(+j)(+i)(-k) |
(+i)(-k)(+j) |
(-k)(+j)(+i) |
(-j)(-i)(-k) |
(-i)(-k)(-j) |
(-k)(-j)(-i) |
Lijst van de permutaties die voldoen aan de reverse regels van Hamilton
|
(-i)(-j)(-k) |
(-j)(-k)(-i) |
(-k)(-i)(-j) |
(+i)(+j)(-k) |
(+j)(-k)(+i) |
(-k)(+i)(+j) |
|
(-j)(+i)(-k) |
(-k)(+j)(-i) |
(-k)(-j)(+i) |
(+i)(-k)(-j) |
(+j)(-i)(-k) |
(-i)(-k)(+j) |
|
(-i)(+j)(+k) |
(+j)(+k)(-i) |
(+k)(-i)(+j) |
(+i)(-j)(+k) |
(-j)(+k)(+i) |
(+k)(+i)(-j) |
|
(-j)(-i)(+k) |
(-i)(+k)(-j) |
(+k)(-j)(-i) |
(+j)(+i)(+k) |
(+i)(+k)(+j) |
(+k)(+j)(+i) |