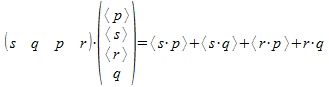
Het creatief product laat verschillende vormen zien van een abstracte structuur die we het creatief product patroon zullen noemen. Dit is een patroon dat ontstaat vanuit twee onafhankelijke standpunten. Het is een abstract inzicht op een analoge manier zoals het patroon van haken dat niet niet beïnvloed wordt door de relatieve keuzen van de betekenis van <> ten opzichte van <<>> en van <p> ten opzichte van p, en op een analoge manier zoals het binair patroon niet beïnvloed wordt door de binaire vrij te kiezen beslissingen (1 ten opzichte van 0, rechts ten opzichte van links). Beide laatste patronen geven aanleiding tot een quaternale benadering: vier mogelijke structuren kunnen eigenlijk dezelfde informatie, hetzelfde patroon, coderen. Willen we een patroon voorstellen, dan moeten we echter een keuze maken. Het patroon van het creatief product leidt ook tot een patroon met vier realisaties. De abstracte overeenkomst kan echter niet quaternaal zijn zoals het begrip gedefinieerd werd: immers, de inbedding van elke onderscheiding maakt geen verschil aangezien elke term uit de som van het creatief product een transformatie is. Toch is hierbij een viervoudige relatie duidelijk die we aangeven door de korte notering in de eerste kolom van de tabel hieronder: dit maakt duidelijk welke vormen de inbedding zijn van elkaar. In de tweede kolom volgt dan de realisatie van het creatief product in zijn twee varianten waarbij het onafhankelijk standpunt (ofwel s•r ofwel p•q) duidelijk wordt, dit standpunt wordt ook duidelijk in de product notering in vijfde kolom (noteer dat er ook een standpunt p•q•r•s kan gedefinieerd worden dat onafhankelijk is van s•r en p•q). In de derde en vierde kolom worden drie interne involuties gedefinieerd (dualeren, toevoegen, orthogonaliseren) als het inbedden van gedeelten van de haakvector die een mogelijke realisatie is van het creatief product patroon.
Orthogonaliseren definiëren we dan als één component van elk standpunt inbedden (en dus twee componenten van de som inbedden)
Globaal inbedden is dan de twee componenten van eenzelfde standpunt inbedden (en dus eveneens twee componenten van de som inbedden)
Dualeren is dan de twee componenten van een geselecteerd standpunt inbedden en één component van het ander standpunt (en dus een component van de som inbedden)
Toevoegen is de inbedding van dualeren: slechts een component van een geselecteerd standpunt inbedden (en dus drie componenten van de som inbedden).
Enkel bij het globaal inbedden doet het er niet toe welk standpunt men inneemt. Dus de unaire relatie van inbedding, en dus “iets anders dan”, is weer de sturende relatie van het patroon.
|
Korte notering |
Creatief product |
Operatie op het creatief product gekozen als start |
Naam voor de operatie (we nemen s•r als standpunt 1 en p•q als standpunt 2) |
Product notering |
Haakuitdrukking |
|
_r•q |
<s•p>⊕<s•q>⊕<r•p>⊕r•q= (<r•p>⊕<s•q>)•<<>>⊕(<r•p>⊕s•q)•s•r= (<r•p>⊕<s•q>)•<<>>⊕(r•p⊕<s•q>)•p•q |
start |
start |
(r•p⊗s•q)s•r= (r•p⊗s•q)<p•q> |
<<<s•r>><r•p>><<s•r><s•q>>↔ <<p•q><r•p>><<<p•q>><s•q>> |
|
_<r•q> |
s•p⊕s•q⊕r•p⊕<r•q>= (r•p⊕s•q)•<<>>⊕(r•p⊕<s•q>)•s•r= (r•p⊕s•q)•<<>>⊕(<r•p>⊕s•q)•p•q |
zowel s als r inbedden=zowel p als q inbedden |
globaal inbedden |
(<r•p>⊗<s•q>)s•r= (<r•p>⊗<s•q>)<p•q> |
<<<s•r>><<r•p>>><<s•r><<s•q>>>↔ <<p•q><<r•p>>><<<p•q>><<s•q>>> |
|
_ r•p |
<s•p>⊕<s•q>⊕r•p⊕<r•q>= (r•p⊕<s•q>)•<<>>⊕(r•p⊕s•q)•<s•r>= (r•p⊕<s•q>)•<<>>⊕(<r•p>⊕<s•q>)•p•q |
r inbedden |
standpunt 1 dualeren = standpunt 1 toevoegen en globaal inbedden = orthogonaliseren en standpunt 2 toevoegen |
(<r•p>⊗s•q)<s•r>= (<r•p>⊗s•q)<p•q> |
<<s•r><<r•p>>><<<s•r>><s•q>>↔ <<p•q><<r•p>>><<<p•q>><s•q>> |
|
_<r•p> |
s•p⊕s•q⊕<r•p>⊕r•q= (<r•p>⊕s•q)•<<>>⊕(<r•p>⊕<s•q>)•<s•r>= (<r•p>⊕s•q)•<<>>⊕(r•p⊕s•q)•p•q |
s inbedden |
standpunt 1 toevoegen = standpunt 1 dualeren en globaal inbedden = orthogonaliseren en standpunt 2 dualeren |
(r•p⊗<s•q>)<s•r>= (r•p⊗<s•q>)<p•q> |
<<s•r><r•p>><<<s•r>><<s•q>>>↔ <<p•q><r•p>><<<p•q>><<s•q>>> |
|
_ s•q |
<s•p>⊕s•q⊕<r•p>⊕<r•q>= (<r•p>⊕s•q)•<<>>⊕(<r•p>⊕<s•q>)•s•r= (<r•p>⊕s•q)•<<>>⊕(r•p⊕s•q)•<p•q> |
q inbedden |
standpunt 2 dualeren = standpunt 2 toevoegen en globaal inbedden =orthogonaliseren en standpunt 1 toevoegen |
(r•p⊗<s•q>)s•r= (r•p⊗<s•q>)p•q |
<<<s•r>><r•p>><<s•r><<s•q>>>↔ <<<p•q>><r•p>><<p•q><<s•q>>> |
|
_<s•q> |
s•p⊕<s•q>⊕r•p⊕r•q= (r•p⊕<s•q>)•<<>>⊕(r•p⊕s•q)•s•r= (r•p⊕<s•q>)•<<>>⊕(<r•p>⊕<s•q>)•<p•q> |
p inbedden |
standpunt 2 toevoegen = standpunt 2 dualeren en globaal inbedden = orthogonaliseren en standpunt 1 dualeren |
(<r•p>⊗s•q)s•r= (<r•p>⊗s•q)<p•q> |
<<<s•r>><<r•p>>><<s•r><s•q>>↔ <<<p•q>><<r•p>>><<p•q><s•q>> |
|
_s•p |
s•p⊕<s•q>⊕<r•p>⊕<r•q>= (<r•p>⊕<s•q>)•<<>>⊕(<r•p>⊕s•q)•<s•r>= (<r•p>⊕<s•q>)•<<>>⊕(r•p⊕<s•q>)•<p•q> |
zowel s als q inbedden=zowel r als p inbedden |
orthogonaliseren |
(r•p⊗s•q)<s•r>= (r•p⊗s•q)p•q |
<<s•r><r•p>><<<s•r>><s•q>>↔ <<<p•q>><r•p>><<p•q><s•q>> |
|
_<s•p> |
<s•p>⊕s•q⊕r•p⊕r•q= (r•p⊕s•q)•<<>>⊕(r•p⊕<s•q>)•<s•r>= (r•p⊕s•q)•<<>>⊕(<r•p>⊕s•q)•<p•q> |
zowel s als p inbedden=zowel r als q inbedden |
orthogonaliseren en globaal inbedden |
(<r•p>⊗<s•q>)<s•r>= (<r•p>⊗<s•q>)p•q |
<<s•r><<r•p>>><<<s•r>><<s•q>>>↔ <<<p•q>><<r•p>>><<p•q><<s•q>>> |
Uit de tabel is duidelijk dat drie van de vier haakvectoren uit de som dezelfde signatuur hebben, het creatief product patroon is dus een 3&1 patroon dat het verder bestuderen waard is.
Het patroon ontstaat uit de vermenigvuldiging van een rijvector en een kolomvector: bijvoorbeeld: <s•p>⊕<s•q>⊕<r•p>⊕r•q kunnen we voorstellen als de vermenigvuldiging van een rijvector en een kolomvector als volgt:
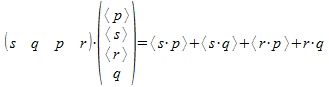
De rijvector en de kolomvector zijn een oneven permutatie van elkaar en drie van de vier componenten zijn elkaars inbedding.