De studie van het algemeen product model leert ons dat de evolutie van een intensiteit van de eenheid (x-x₀) op een meer abstract niveau kan gemodelleerd worden door de evaluatie van (x-x₀)Π_ν(1+κ) op het punt n en k, waarbij zowel ν als κ variabelen zijn. We kunnen hierbij de stappen in een evolutie modelleren door ν als een geheel getal te beschouwen dat enkel maar toeneemt terwijl κ invariant is, maar we kunnen de stappen ook modelleren door ν als invariant te beschouwen terwijl κ varieert, en de evolutie dus een mengeling van een positief feedback proces en een negatief feedback proces.

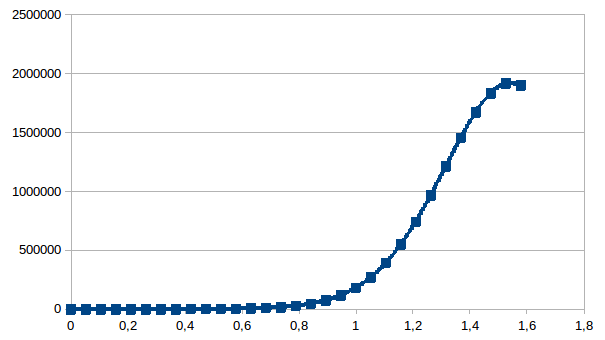
We zullen nu veronderstellen dat ν niet varieert en gelijk is aan 1 en dat κ varieert tussen -1 en +1 zoals gemodelleerd wordt door een sinusoïde. Dus (1+κ) varieert tussen 0 en 2 (en dit is niet verschillend van (1-κ) die varieert tussen 2 en 0). Dat gebeurt in stappen die fracties zijn van 2π en die geordend zijn zoals de sporen die in de tijd gevonden worden. Die fracties modelleren dan een hoek en die modelleert dan een herhaaldelijke opeenvolging van zekerheid en maximale onzekerheid. Het gevolg hiervan is dat de intensiteit, dus het product Π(1+κ), gelijk zal zijn aan 0 afhankelijk van de fase, de fase die altijd een fractie is van het getal π zodanig dat de nul nooit bereikt kan worden (geen enkele fractie van een, in dit geval irrationaal, getal kan gelijk zijn aan 0). We kunnen maar één maal een nul kiezen, dat is bij het begin van de evolutie en dan zal, bij het modelleren als cosinus, en dus cos(0)=1, de intensiteit gelijk zijn aan 2. De verdere evolutie van de intensiteit zal afhangen van de fase. Wanneer we de intensiteit dus uitzetten ten opzichte van de fase dan zal er één piek te vinden zijn die voor de cosinus zal optreden rond π/2, of dus ongeveer 1,5707963268.

Hier tonen we drie simulaties in 30 stappen. De eerste heeft π/2, of dus ongeveer 1,5707963268 helemaal op het einde van het aantal stappen, de volgende heeft die fase ongeveer centraal, en de laatste aan het begin.

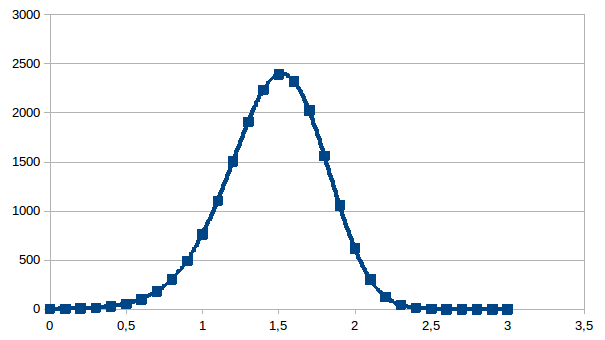
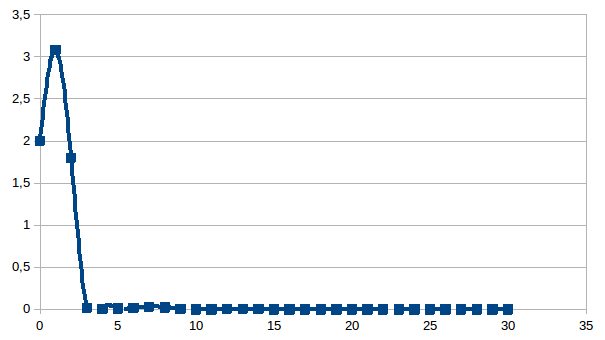
Het verschil tussen de drie simulaties is de golflengte van de trilling (beter: de waarnemingsresolutie). In het eerste geval wordt op die 30 stappen ongeveer een vierde van een golflengte doorlopen, in het tweede geval ongeveer een halve golflengte, in het laatste geval zijn het er bijna 5 golflengtes.