Met behulp van de meest eenvoudige modellen in een som model hebben we al heel complex gedrag kunnen simuleren dat onder andere kan geïnterpreteerd worden dan dat een intensiteit heel plots kan veranderen. Dit noemen we een omslagpunt. Omslagpunten zijn anticipeerbaar, ze hoeven niet het gevolg te zijn van een willekeurige beslissing. Door deze manier van modelleren als een universeel som gedrag kunnen we dus modelleren dat sommige processen pas na een zekere tijd “reageren” op veranderingen.

Een omslagpunt kunnen we ook in een product model genereren en een product model kunnen we ook interpreteren als het modelleren van simultaneïteit. Dit maakt het mogelijk om processen en logica met elkaar te koppelen, evolutie te modelleren en om de werkelijkheid met stochastische parameters te karakteriseren.

Voorbeelden van anticipatie

De abrupte verandering van eigenwaarde herkennen we als de algemene beschrijving van een anticipatie: “indien …, dan..., zo niet...” (bijvoorbeeld: indien de intensiteit die waarde bereikt heeft, dan...; of: indien de volgende tijd verlopen is, dan...; of: indien een ander individu gemeten wordt, dan... enz...). De nieuwe anticipatie introduceert een discontinuïteit, en elke processtap kan discontinu zijn. Wanneer de karakteristiek van de feedback eveneens verandert bij de discontinuïteit, dan zijn er in totaal 16 mogelijke patronen voor één discontinue stap na de start. Anticipatie is natuurlijk een toepassing van logische relaties.

We geven hiervan een aantal voorbeelden waarbij we de eigenwaarden zo kiezen dat de discontinuïteit goed merkbaar is. We hebben de 16 patronen binair gecodeerd.

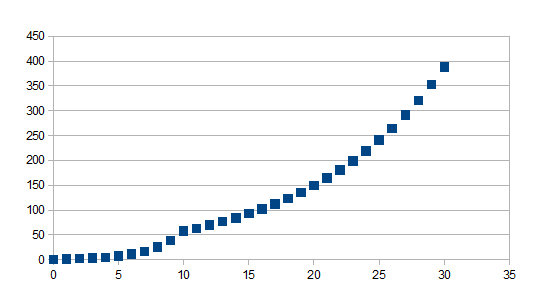
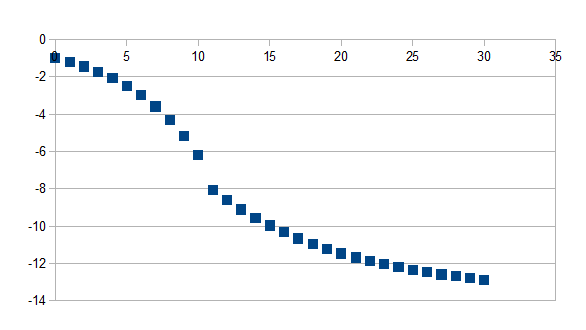Indien de tijdstap groter is dan t geldt (1+k)t(1+k')n-t zo niet geldt (1+k)t waarbij k=0,5 en k'=0,1 en t=10 voor 30 stappen

Positieve feedback in de positieve richting gevolgd door positieve feedback in de positieve richting met een kleinere eigenwaarde in absolute waarde vanaf stap t.

(++++)



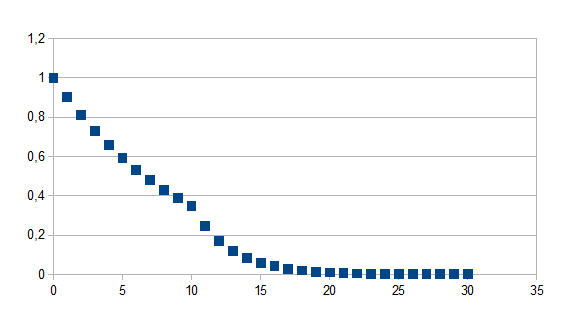
Indien de tijdstap groter is dan t geldt (1+k)t(1+k')n-t zo niet geldt (1+k)t waarbij k=-0,1 en k'=-0,3 en t=10 voor 30 stappen

Negatieve feedback in de negatieve richting gevolgd door negatieve feedback in de negatieve richting met een grotere eigenwaarde in absolute waarde vanaf stap t.

(----)



Indien de tijdstap groter is dan t geldt -(1+k)t(1+k')n-t zo niet geldt -(1+k)t waarbij k=0,1 en k'=0,02 en t=10 voor 30 stappen

Positieve feedback in de negatieve richting gevolgd door positieve feedback in de negatieve richting met een kleinere eigenwaarde in absolute waarde vanaf stap t.

(+-+-)



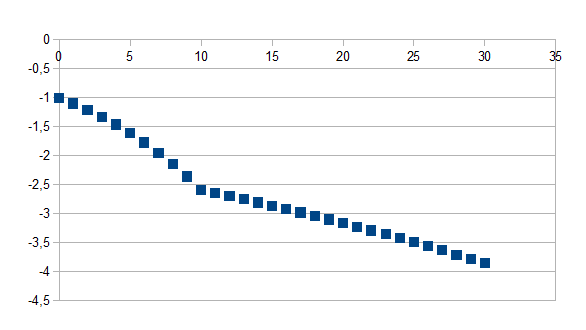
Indien de tijdstap groter is dan t geldt -(1+k)t(1+k')n-t zo niet geldt -(1+k)t waarbij k=-0,1 en k'=-0,3 en t=10 voor 30 stappen

Negatieve feedback in de positieve richting gevolgd door negatieve feedback in de positieve richting met een grotere eigenwaarde in absolute waarde vanaf stap t.

(-+-+)



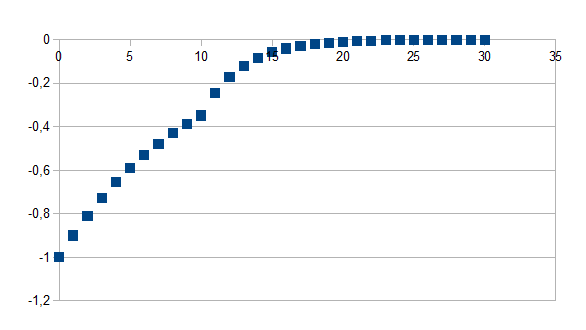
Indien de tijdstap groter is dan t geldt (1+k)t(1+k')n-t zo niet geldt (1+k)t waarbij k=0,5 en k'=-0,1 en t=10 voor 30 stappen

Positieve feedback in de positieve richting gevolgd door negatieve feedback in de negatieve richting met een kleinere eigenwaarde in absolute waarde vanaf stap t.

(++--)



Indien de tijdstap groter is dan t geldt (1+k)t(1+k')n-t zo niet geldt (1+k)t waarbij k=-0,1 en k'=0,15 en t=10 voor 30 stappen

Negatieve feedback in de negatieve richting gevolgd door positieve feedback in de positieve richting met een grotere eigenwaarde in absolute waarde vanaf stap t.

(--++)



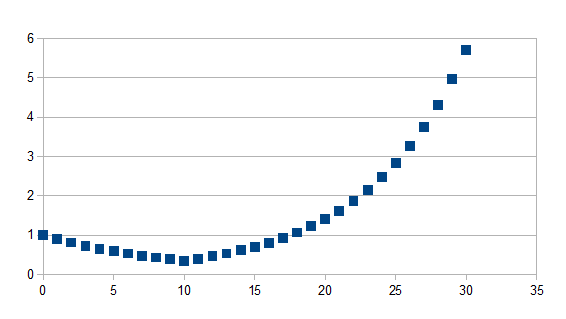
Indien de tijdstap groter is dan t geldt -(1+k)t(1+k')n-t zo niet geldt -(1+k)t waarbij k=0,1 en k'=-0,2 en t=10 voor 30 stappen

Positieve feedback in de negatieve richting gevolgd door negatieve feedback in de positieve richting met een grotere eigenwaarde in absolute waarde vanaf stap t.

(+--+)



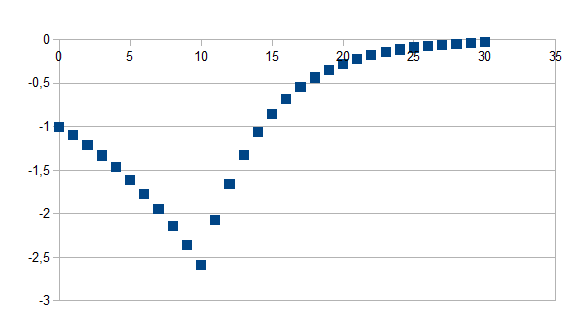
Indien de tijdstap groter is dan t geldt -(1+k)t(1+k')n-t zo niet geldt -(1+k)t waarbij k=-0,1 en k'=0,1 en t=10 voor 30 stappen

Negatieve feedback in de positieve richting gevolgd door positieve feedback in de negatieve richting met een zelfde eigenwaarde in absolute waarde vanaf stap t.

(-++-)



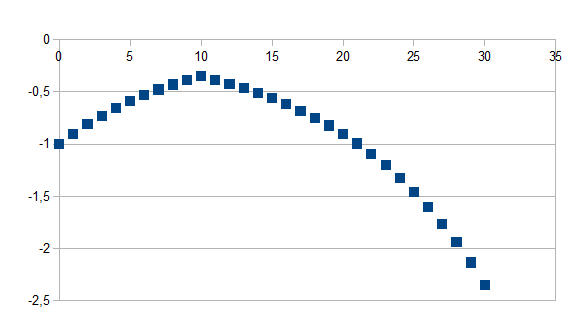
Indien de tijdstap groter is dan t geldt (1+k)t+(1+k)t+1-(1+k)t(1+k')n-t zo niet geldt (1+k)t waarbij k=0,5 en k'=0,1 en t=10 voor 30 stappen

Positieve feedback in de positieve richting gevolgd door positieve feedback in de negatieve richting met een kleinere eigenwaarde in absolute waarde vanaf stap t

Merk op dat voor punten groter dan t de waarde (1+k)t+(1+k)t+1 een constante is.



(+++-)



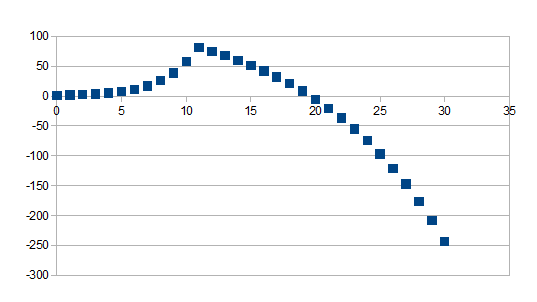
Indien de tijdstap groter is dan t geldt (1+k)t+(1+k)t+1-(1+k)t(1+k')n-t zo niet geldt (1+k)t waarbij k=0,5 en k'=-0,1 en t=10 voor 30 stappen

Positieve feedback in de positieve richting gevolgd door negatieve feedback in de positieve richting met een kleinere eigenwaarde in absolute waarde vanaf stap t

Merk op dat voor punten groter dan t de waarde (1+k)t+(1+k)t+1 een constante is.

(++-+)



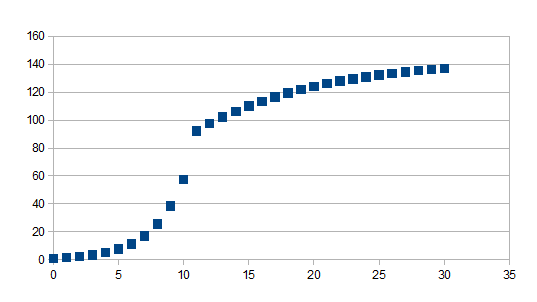
Indien de tijdstap groter is dan t geldt -(1+k)t-(1+k)t+1+(1+k)t(1+k')n-t zo niet geldt -(1+k)t waarbij k=0,2 en k'=0,1 en t=10 voor 30 stappen

Positieve feedback in de negatieve richting gevolgd door positieve feedback in de positieve richting met een kleinere eigenwaarde in absolute waarde vanaf stap t

Merk op dat voor punten groter dan t de waarde -(1+k)t-(1+k)t+1 een constante is.

(+-++)



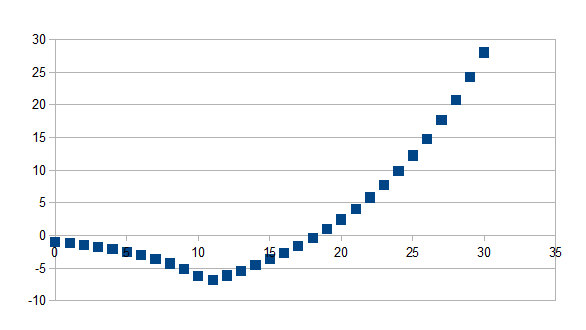
Indien de tijdstap groter is dan t geldt -(1+k)t-(1+k)t+1+(1+k)t(1+k')n-t zo niet geldt -(1+k)t waarbij k=-0,2 en k'=0,1 en t=10 voor 30 stappen

Negatieve feedback in de positieve richting gevolgd door positieve feedback in de positieve richting met een kleinere eigenwaarde in absolute waarde vanaf stap t

Merk op dat voor punten groter dan t de waarde -(1+k)t-(1+k)t+1 een constante is.

(-+++)



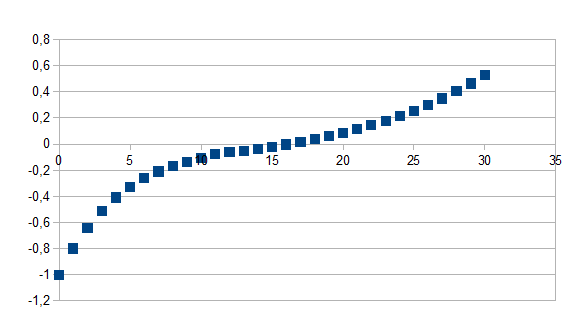
Indien de tijdstap groter is dan t geldt (1+k)t+(1+k)t+1-(1+k)t(1+k')n-t zo niet geldt (1+k)t waarbij k=-0,2 en k'=-0,5 en t=10 voor 30 stappen

Negatieve feedback in de negatieve richting gevolgd door negatieve feedback in de positieve richting met een grotere eigenwaarde in absolute waarde vanaf stap t

Merk op dat voor punten groter dan t de waarde (1+k)t+(1+k)t+1 een constante is.

(---+)



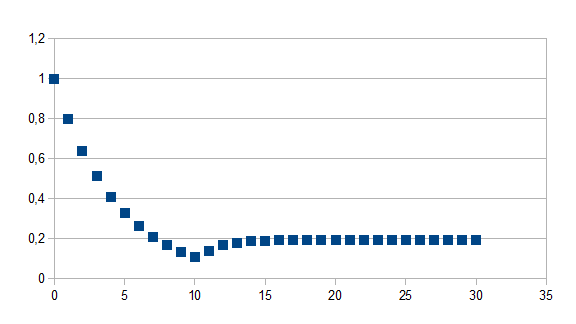
Indien de tijdstap groter is dan t geldt (1+k)t+(1+k)t+1-(1+k)t(1+k')n-t zo niet geldt (1+k)t waarbij k=-0,2 en k'=0,2 en t=10 voor 30 stappen

Negatieve feedback in de negatieve richting gevolgd door positieve feedback in de negatieve richting met een zelfde eigenwaarde in absolute waarde vanaf stap t

Merk op dat voor punten groter dan t de waarde (1+k)t-1 een constante is.

(--+-)



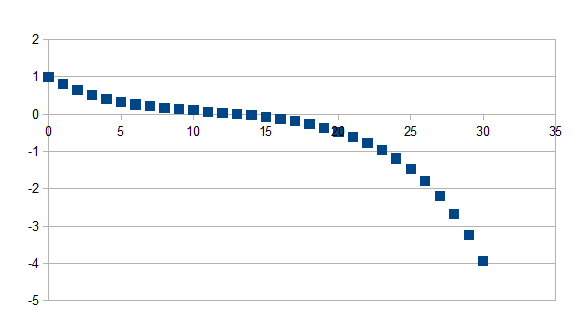
Indien de tijdstap groter is dan t geldt -(1+k)t-(1+k)t+1+(1+k)t(1+k')n-t zo niet geldt -(1+k)t waarbij k=-0,2 en k'=-0,1 en t=10 voor 30 stappen

Negatieve feedback in de positieve richting gevolgd door negatieve feedback in de negatieve richting met een kleinere eigenwaarde in absolute waarde vanaf stap t

Merk op dat voor punten groter dan t de waarde -(1+k)t-(1+k)t+1 een constante is.

(-+--)



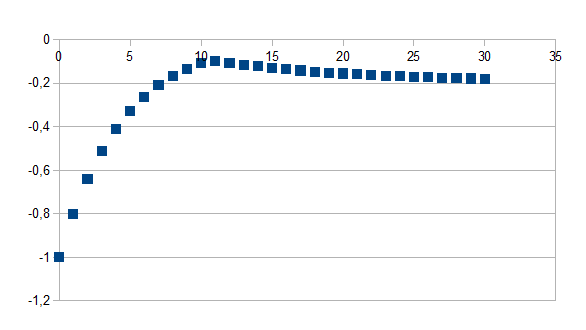
Indien de tijdstap groter is dan t geldt -(1+k)t-(1+k)t+1+(1+k)t(1+k')n-t zo niet geldt -(1+k)t waarbij k=0,2 en k'=-0,1 en t=10 voor 30 stappen

Positieve feedback in de negatieve richting gevolgd door negatieve feedback in de negatieve richting met een kleinere eigenwaarde in absolute waarde vanaf stap t

Merk op dat voor punten groter dan t de waarde -(1+k)t-(1+k)t+1 een constante is.

(+---)



Een eigenwaarde die verandert op een bepaalde tijdstap kunnen we interpreteren als het gevolg van een interactie van een spontaan proces met een ander (spontaan) proces vanaf die bepaalde tijdstap of vanaf een bepaalde densiteit aan individuen. Inderdaad: intensiteiten kunnen genormaliseerd worden op een gemeenschappelijke eenheid.

Evolutie

Het product (x-x0)Πν(1+κ) kan dus modelleren dat sommige (1+k)m constanten zijn naast de constante (x-x0). Zij zijn dan entiteiten (eenheden, onvermijdelijk begrensd, die in de loop van het onvermijdelijk monotoon doorgaande proces niet meer zullen gehalveerd worden). De begrenzing zullen we verder onderzoeken. We kunnen dus het product (x-x0)Πν(1+κ) ook interpreteren als de uitdrukking dat enkel “actieve eigenwaarden” een rol spelen in het gedrag, of, als we dat met exponenten willen uitdrukken, dat enkel vanaf een bepaalde lading activiteit waarneembaar is. De eigenwaarden “die niet meer actief zijn”, zijn eigenwaarden die niet meer tot een exponent verheven worden, ze zijn invarianten voor de totale verandering en zo modelleren we een evolutie in de tijd als causale relaties.

Een voorbeeld hiervan is massa. Uiteraard moeten we voor veel modellen van gedrag rekening houden met de massa van de betrokken materie, maar die massa is voor dat gedrag dan een constante. Dit geldt uiteraard evenzeer voor al die andere aspecten die nu invariant zijn (de valentie van molecules, het DNA, de sociale afspraken enz…) en waarbij we ons voorstellen dat ze ooit ontstaan moeten zijn in het grote verhaal van de evolutie dat we aan elkaar vertellen.

Stochastische modellen

Het product geeft ook zin aan stochastische modellen. We kunnen hierbij verschillende soorten modelleren met een a priori onvoorspelbaar gedrag, gedrag dat we evalueren op het niveau van de soort, niet op het niveau van een individu. De individuen van de globale soort worden gekarakteriseerd door een gemiddelde eigenwaarde en een spreiding hierop. We gebruiken hiervoor de eigenwaarde κ en de spreiding erop en dat voor ν individuen, waarbij het gedrag van de individuen in de soort a priori ongekend is maar kan ondergebracht worden in gelijkaardige categorieën. De globale soort wordt dan gekarakteriseerd door (x-x0)Πν(1+κ). Het aantal stappen die elkaar uitsluiten is hier niet meer en niet minder dan het aantal individuen van een bepaalde soort die elkaar uitsluiten en simultaan actief zijn.

Waarnemen en collaps

Een abrupt veranderende eigenwaarde zien we telkens wanneer een waarneming een oorspronkelijke verwachting (prior) verandert in een grotere verwachting (posterior) ofwel wanneer een waarneming een oorspronkelijke verwachting onmogelijk te ervaren maakt. Inderdaad beide zijn verbonden door de Bayesiaanse relatie P(<<A>i>/(Ej/A0)=κP(<<A>i>/A0). Vooraleer Ej waargenomen werd dank zij een geproduceerd spoor was er een bepaalde verwachting voor het hypothetisch punt <<A>i> gegeven door i-1. Bij de waarneming van Ej verandert de verwachting abrupt, inderdaad is de waarschijnlijkheid dat Ej waargenomen wordt bij het waarnemen van Ej gelijk aan 1. De opgespannen tralie collapst naar een tralie die door minder onderscheidingen opgespannen wordt, het hypothetisch punt wordt maar door een fractie van het aantal onderscheidingen i opgespannen waarbij dus de andere onderscheidingen irrelevant worden en dus is de waarschijnlijkheid dat <<A>i> waargenomen wordt groter geworden.