We hebben begrepen dat k(x-x₀) evenzeer als (x-x₀) als een constante kan beschouwd worden. Verschillende k_m(x-x₀) zullen zich dan als eenheden gedragen. We hebben de entiteiten die gekarakteriseerd worden door k_m(x-x₀) telbare deelaspecten of buffers genoemd van het spontaan proces 1(x-x₀). Elk deelaspect m zal op een bepaalde stap in het proces een intensiteit hebben (x-x₀)(1±k_m)ⁿ. We veronderstellen daarbij dat 0<k_m<1. Dit veronderstelt veel over de telbare deelaspecten van het totaal proces en dit zullen we nu onderzoeken.

We zullen eerst veronderstellen dat de dynamiek van deelaspecten zodanig kan zijn dat een proces niet meer verandert: een evenwicht is bereikt. De veronderstelling die we daarvoor nodig hebben is dat de processen elkaar moeten kunnen opheffen, zodanig dat een of andere eenheid stabiel blijft in de tijd en er dus van evenwicht en stabiliteit sprake kan zijn. We kijken welke van de operaties “som”, “verschil”, “product” daarvoor in aanmerking komt.

Een som van positieve en negatieve feedback is een interactie die geen evenwicht bereikt

We veronderstellen twee interagerende processen met dezelfde eenheid (x-x₀): een positieve feedback met constante eigenwaarde k en een negatieve feedback met dezelfde constante eigenwaarde. We veronderstellen dat beide processen onafhankelijk zijn zodanig dat de som van de processen een betekenis heeft. Na één stap wordt de waarde (x-x₀)(1+k) bereikt in het eerste geval en (x-x₀)(1-k) in het tweede geval. We vragen ons nu af onder welke voorwaarden beide processen een evenwicht kunnen bereiken.

De som van de waarde (x-x₀)(1+k) en (x-x₀)(1-k) is (x-x₀)2. Na de volgende stap wordt de waarde (x-x₀)(2+k) bereikt in het eerste deelproces en (x-x₀)(2-k) in het tweede deelproces, beide zijn onafhankelijk van elkaar dus de som van beide waarden is (x-x₀)4. Na de volgende stap wordt de waarde (x-x₀)(4+k) bereikt in het eerste deelproces en (x-x₀)(4-k) in het tweede deelproces. De som van beide waarden is (x-x₀)8 enz…

De opeenvolgende intensiteiten van (x-x₀) in het proces dat door deze som gemodelleerd wordt zijn de getallen 2ⁿ. Dit is het aantal simultane punten in een tralie (zie de paragraaf “partiële orde”) bij het doorlopen van de tralie van niveau tot niveau. Juist dat is wat we een spontaan proces genoemd hebben dat gemodelleerd wordt door de toenemende disjunctie x_n van elkaar uitsluitende atomaire toestanden gelabeld met de stappen van de doorlopen tijd, dus bij een volgende tijdstap wordt een volgend niveau bereikt. Het proces dat door deze som gemodelleerd wordt komt ook overeen met een positieve feedback met eigenwaarde k=1.

Wanneer we de interactie van twee processen modelleren als een som van positieve en negatieve feedback bij elke stap bereikt het proces dus nooit een evenwicht maar een intensiteit die uiteindelijk groter kan worden dan de waarnemingsresolutie (groter dan nul) en de intensiteit blijft groeien tot de intensiteit het interval van de waarnemingsresolutie verlaat. Uiteindelijk kunnen de intensiteiten niet meer geordend worden. Dit geldt zowel alvorens stap 1 gezet wordt als na stap n en dat is agens-in-context afhankelijk. Dat is de operationele betekenis van oneindig met zijn invers: nul. Indien er niet meer kan geordend worden is elke anticipatiepoging zinloos, wat gebeurt is willekeurig, het ervarend agens-in-context kan datgene wat gebeurt niet meer beïnvloeden of sturen.

Een verschil van positieve en negatieve feedback is een interactie die geen evenwicht bereikt maar wel een constante snelheid

Het verschil van de waarde (x-x₀)(1+k) en (x-x₀)(1-k) is (x-x₀)2k. Na de volgende stap wordt de waarde (x-x₀)(2k+k) bereikt in het eerste deelproces en (x-x₀)(2k-k) in het tweede deelproces. Het verschil van beide waarden is (x-x₀)2k. Na de volgende stap wordt de waarde (x-x₀)(2k+k) bereikt in het eerste deelproces en (x-x₀)(2k-k) in het tweede deelproces. De som van beide waarden is (x-x₀)2k enz…

We kunnen dit ook als volgt begrijpen: na één stap in de positieve feedback is de intensiteit (x-x₀)(1+k) en die wordt niet teniet gedaan door het verschil met een negatieve feedback na één stap, het verschil is namelijk (x-x₀)(1+k)-(x-x₀)(1-k)=2k(x-x₀) maar vervolgens blijft deze intensiteit voor een onveranderlijke eigenwaarde k stabiel. Hier zien we een factor 2 ontstaan die ook nog op andere plaatsen als gevolg een modellering van evenwicht zal opduiken, maar ook de factor k, de verhouding die stabiel blijft tussen twee opeenvolgende toestanden.

Een product van positieve en negatieve feedback als interactie

De interactie van positieve en negatieve feedback kunnen we ook modelleren als een product. Positieve en negatieve feedback kunnen elkaar opheffen met de geschikte normalisatiefactor (1-k²)^-n. Inderdaad er geldt de tautologie (1+k)ⁿ(1-k)ⁿ(1-k²)^-n = 1ⁿ en dit geldt voor elke n, dus bij elke stap is er een andere normalisatiefactor. Elke 1 is uit te drukken in functie van twee andere getallen p en q op de volgende manier: (p+q)(p-q)(p²-q²)^-1 =1. Die twee getallen verwijzen naar metingen van twee met elkaar gerelateerde intensiteiten van de betrokken variabele, dit is hoe een eenheid kan uitgebreid en uitgedrukt worden ook in andere toepassingen en hoe dubbelgetallen kunnen genormaliseerd worden. Dit is uiteindelijk het gevolg van het verschil dat we kunnen en moeten maken tussen een eenheid en een intensiteit en de manier waarop we gekozen eenheden (en dus de keuze voor een schaal) in elkaar kunnen uitdrukken.

Om dit te tonen beschouwen we nu enkel de positieve feedback in de positieve zin en de negatieve feedback in de negatieve zin met een 0<k<1.

We expliciteren nu ook het nulpunt als anti-doel voor positieve feedback en het nulpunt als doel voor negatieve feedback omdat dit een uitgebreider patroon van normalisatie duidelijk maakt dat we verder zullen ontwikkelen.

We kunnen de factor (1-k²)^-n op verschillende manieren toewijzen aan de twee soorten feedback. Bijvoorbeeld: we kunnen de positieve feedback nu normaliseren als (1+k)ⁿ(1-k²)^-0,5n en de negatieve feedback als (1-k)ⁿ(1-k²)^-0,5n. We veronderstellen dan dat beide een even grote invloed uitoefenen (0,5n + 0,5n = n). In het algemeen kunnen we dit voorstellen als (1+k)ⁿ(1-k²)^-tn en (1-k)ⁿ(1-k²)^-(1-t)n. We zullen t de lading van de feedback noemen omdat t ofwel positief, ofwel negatief kan zijn.

We merken nu ook op dat dit ook zal gelden voor een andere keuze van de termen (1+k) en (1-k), bijvoorbeeld bij de keuze (p+q) versus (p-q) en de relatie dus wordt: (p+q)ⁿ(p-q)ⁿ(p²-q²)^-n = 1. Hetzelfde zal uiteraard ook gelden als men stelt dat 1+k=r en 1-k=s (en dus dat r+s=2, r-s=2k, s-r=-2k en (r+s)(r-s)=4k), zodanig dat de twee genormaliseerde intensiteiten voor te stellen zijn als rⁿ(rs)^-tn en sⁿ(rs)^-(1-t)n met t de lading van feedback. Uiteraard geldt rⁿ(rs)^-tnsⁿ(rs)^-(1-t)n=1.

De tautologie (x-x₀)(1+k)ⁿ(1-k)ⁿ(1-k²)^-n = (x-x₀)1ⁿ kunnen we dus interpreteren als de eenheid 1(x-x₀) (k=1) die het spontaan proces meemaakt waar twee processen elkaar tegenwerken, eenheid die bij elke stap onveranderd blijft. Deze 1 is de eenheid zelf die stabiel blijft en die eenheid is altijd te construeren met behulp van minimaal twee getallen. De dynamiek kunnen ons dan voorstellen als een “steady state” proces waarbij een buffer niet meer van intensiteit verandert, zoals bij de eenheid van een volle emmer water die onder de kraan staat waarbij alle water dat toegevoegd wordt wegloopt. Toevoegen is positieve feedback voor de accumulatie in de buffer, hoe meer water toestroomt, hoe meer water in de buffer. Weglopen is negatieve feedback voor de accumulatie in de buffer, hoe meer water wegloopt, hoe minder water in de buffer. We beschouwen dit proces als een (vector)product van positieve (“1+k”) en negatieve feedback (“1-k”) en we kunnen zeggen dat ze beide “in fase” zijn omdat de tautologie geldt voor elke stap. In het voorbeeld van de emmer water is de eenheid van de k een fractie van de maximaal mogelijke stroom die met die emmer een evenwicht kan bereiken, immers het volume van een nog grotere stroom kan niet meer in de emmer (en simultaan eruit). Dit is duidelijk als volgt te zien: k (dus (r-s)/2) is gerelateerd aan de eenheid van het spontaan proces waar het deel van uitmaakt als 1 (deze 1 is niet anders dan (r+s)/2). Dus er geldt dat k=(r-s)/(r+s). Dit is de verhouding van een verschil tot een som die maximaal is, bijvoorbeeld twee volumes r en s waarbij r+s maximaal is. We kunnen hier nog andere voorbeelden van geven: neem als eenheid de totale energie, een som van kinetische (r) en potentiële (s) energie, dan wordt k gegeven door het verschil tussen kinetische en potentiële energie, en dat is een component van de intensiteit “actie”. Het getal k=(r-s)/(r+s) kunnen we ook interpreteren als een klassieke snelheid waarbij de noemer de tijd voorstelt die enkel kan toenemen en dus nu een maximum bereikt heeft. Deze verhouding gebruikt de notering die we voor “x intervallen” en “t intervallen” introduceerden: x₀₁=-x₁₀=(n₀-n₁) en t₀₁=t₁₀=(n₀+n₁) en alle gevolgen die we hiervan afgeleid hebben zijn ook van toepassing op feedback processen.

En uiteraard: 1ⁿ kunnen we schrijven als e^{n.(ln(1-k)+ln(1+k)-ln(1-k²))} en er geldt voor elke n: ln(1-k)+ln(1+k)=ln(1-k²)

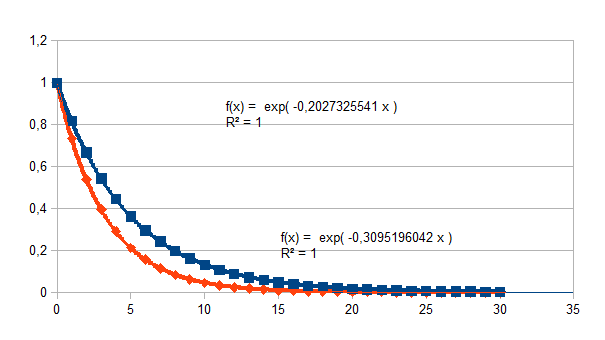
De genormaliseerde formule levert de volgende grafieken op, we kiezen voor de grafiek van een negatieve feedback in de negatieve zin als voorbeeld: (1-k)ⁿ(1-k²)^-0,5n (lading gelijk aan 0,5) met k=0,2 (vierkant) en k=0,3 (ruit) met dertig stappen in de tijd.

We herkennen de negatieve feedback aan de negatieve exponent van e. Merk op: (1-k)ⁿ(1-k²)^-0,5n is niet anders dan e^{n.ln(1-k)-0,5n.ln(1-k^2)} en in de grafiek is de overeenkomstige formule weergegeven.

We kunnen natuurlijk ook de vergelijking maken tussen de grafieken voor andere ladingen, bijvoorbeeld voor de negatieve feedback (1-k)ⁿ(1-k²)^-0,2n (vierkant, lading 0,2) en (1-k)ⁿ(1-k²)^-0,8n (ruit, lading 0,8).

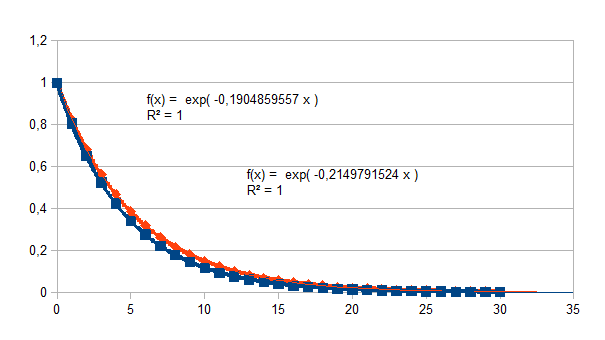
Die relaties zullen dan met de complementaire positieve feedback (respectievelijk (1+k)ⁿ(1-k²)^-0,8n en (1+k)ⁿ(1-k²)^-0,2n) de eenheid vormen.

Om de complementaire negatieve en positieve feedback op de schaal van een grafiek te krijgen kunnen we natuurlijk maar een klein gedeelte van de processtappen (de “tijdlijn”) tonen, we kiezen hieronder voor een resolutie van 0,25. Hieronder de grafiek voor negatieve (vierkant, (1-0,25k)^0,25n(1-(0,25k)²)^-0,5*0,25n) en positieve (ruit, (1+0,25k)^0,25n(1-(0,25k)²)^-0,5*0,25n) feedback met k=0,2 die evenveel lading hebben.

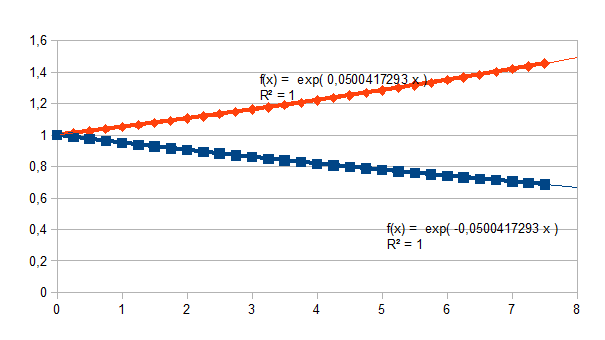
Uiteraard geldt dat 1=(1-0,25k)^0,25n(1-(0,25k)²)^-0,5*0,25n(1+0,25k)^0,25n(1-(0,25k)²)^-0,5*0,25n. Het product van beide levert voor elke stap de eenheid op (de som van beide exponenten is nul).

Hieronder de grafiek voor k=0,2 en resolutie 0,25 maar met een lading van 0,999 voor de negatieve feedback en een lading van 0,001 voor de positieve feedback. En dus ook: 1=(1+0,25k)^0,25n(1-(0,25k)²)^-0,001*0,25n(1-0,25k)^0,25n(1-(0,25k)²)^-0,999*0,25n.

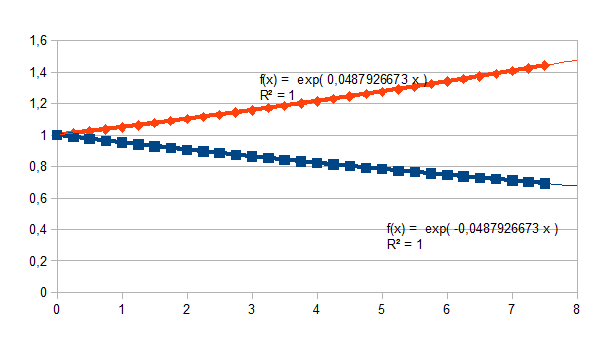
Merk op dat de lading een kleine impact heeft.

Hieronder de vergelijking van het product van beide grafieken (vierkant datapunt), product dat exact 1 is, en het gemiddelde van beide grafieken met de kwadratische vergelijking ervan.

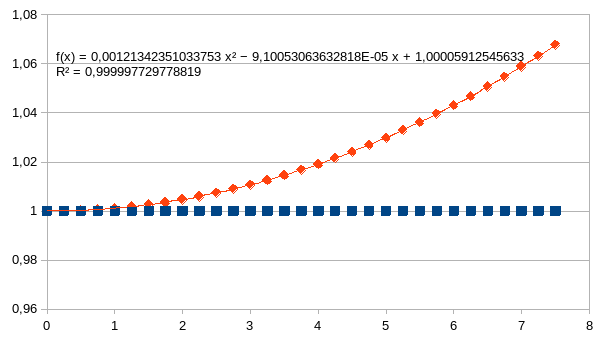
Wanneer we nu als voorbeeld enkel de grafiek nemen van de negatieve feedback dan is duidelijk te zien dat het verband tussen de intensiteiten nagenoeg lineair is. We hebben hieronder de lineaire benadering weergegeven van de exponentiële curve en de correlatiecoëfficiënt R² voor die benadering.

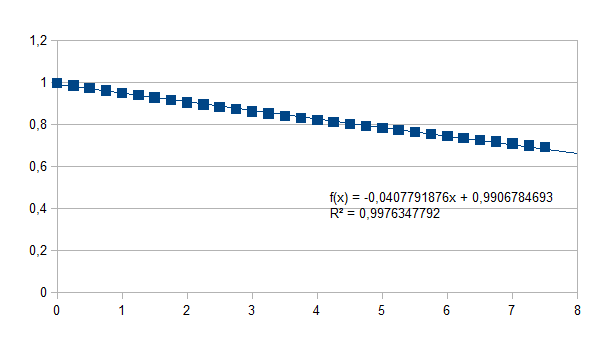
We kunnen er dus altijd van uit gaan dat een relatie tussen twee gemeten parameters die in een eerste benadering als lineair gemodelleerd wordt, een goede benadering is voor een feedback proces met kleine eigenwaarde, uiteraard ook gebonden aan de resolutie van de waarneming van de parameters. Als we aan een proces op het eerste gezicht een lineair verband kunnen waarnemen tussen de intensiteit en de processtap dan modelleren we hiermee een constante snelheid en dat is dus maar een eerste benadering.

Uitbreiding

Feedbackproces met negatieve machten

Aangezien geldt dat (1+k)ⁿ(1-k)ⁿ(1-k²)^-n = 1ⁿ en dit voor elke n, kan een positieve feedback ook voorgesteld worden door een genormaliseerde (1-k)^-n, inderdaad (1+k)ⁿ =(1-k²)ⁿ(1-k)^-n en natuurlijk volledig gelijkaardig voor een negatieve feedback als (1-k)ⁿ =(1-k²)ⁿ(1+k)^-n.

We kunnen dus schrijven (1+k)ⁿ ∝(1-k)^-n en (1-k)ⁿ ∝(1+k)^-n.

Ladingen

De ladingen bepalen of de resulterende intensiteit de evolutie vertoont van positieve of negatieve feedback. Immers: we merken op dat we positieve feedback en negatieve feedback door een geschikte keuze van ladingen in elkaar kunnen transformeren. Noem p de lading die we relateren met de positieve feedback, en q de lading die we relateren met de negatieve feedback en stel (1+k)ⁿ(1-k²)^-pn=(1-k)ⁿ(1-k²)^-qn

(1+k)(1-k²)^-p=(1-k)(1-k²)^-q

(1+k)(1-k)^-1=(1-k²)^p-q

(1+k)(1-k)(1-k)^-2=(1-k²)^p-q

(1-k²)(1-k)^-2=(1-k²)^p-q

(1-k)^-2=(1-k²)^p-q-1

-2ln(1-k)=(p-q-1)ln(1-k²)

-2ln(1-k)/ln(1-k²)=p-q-1

1+q-2ln(1-k)/ln(1-k²)=p

Wanneer we op deze manier de lading p van de positieve feedback vervangen door de relatie tussen de lading q van de negatieve feedback en eigenwaarde k, relatie gegeven door 1+q-2ln(1-k)/ln(1-k²), dan zullen beide feedback processen identiek zijn.

We illustreren dit met twee voorbeelden. Bij de keuze van q=11 en k=0,099 krijgen we een positieve feedback als resultaat (vierkant en samenvallend hiermee een ruit) en met het product van positieve en negatieve feedback krijgen we dan het kwadraat ervan (driehoek)

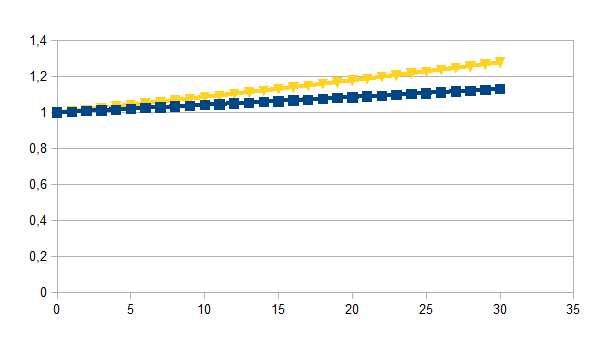
Bij de keuze van q=11 en k=0,090 krijgen we een negatieve feedback als resultaat (vierkant en samenvallend hiermee een ruit) en met het product van positieve en negatieve feedback krijgen we dan het kwadraat ervan (driehoek)

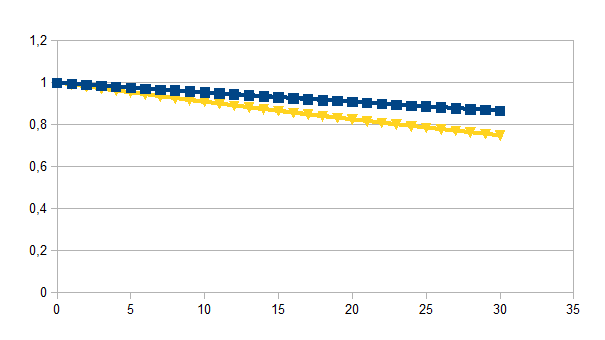
Door één lading te manipuleren bij vaste eigenwaarde, of door enkel de eigenwaarde te manipuleren bij vaste lading, zijn we dus in staat het soort proces te modelleren. Indien een ander proces als resultaat zou hebben dat de intensiteit van de ladingen veranderd wordt of dat de eigenwaarde veranderd wordt, dan zullen we complexe patronen kunnen zien verschijnen.

Normalisatie van meerdere deelaspecten

De uitbreiding naar meerdere deelaspecten die elk door een eventueel andere eigenwaarde gekarakteriseerd kunnen worden ligt nu voor de hand. Normalisatie maakt het mogelijk om een willekeurig aantal deelprocessen te modelleren die simultaan het resultaat beïnvloeden. De ladingen geven de relatieve invloed van de deelprocessen. We merken daartoe op dat we tot nu toe een specifiek geval onderzocht hebben van elkaar tegenwerkende processen: (1+k)ⁿ(1-k)ⁿ(1-k²)^-n = 1ⁿ. Uiteraard geldt ook dat (1+k)ⁿ(1+k)ⁿ(1+2k+k²)^-n = 1ⁿ. Natuurlijk kunnen we dit ook uitbreiden door verschillende k te nemen, we geven een voorbeeld met twee verschillende: (1+k₀)ⁿ(1+k₁)ⁿ(1+k₀+k₁+k₀k₁)^-n = 1ⁿ, en natuurlijk moeten we ons niet beperken tot twee deelaspecten, zodanig dat een algemene normalisatie van de simultane evolutie van m entiteiten met een eigenwaarde k_m gegeven wordt door Π_m(1+k_m)ⁿΠ_m(1+k_m)^-n=1^-n waarbij Π_m staat voor het product van 1 tot en met m en waarbij elke k_m zowel positief als negatief kan zijn.

De invloed die elke eigenwaarde uitoefent op de uiteindelijke intensiteit wordt bepaald door de lading van de normalisatiefactor van elke individuele (1+k_m), namelijk t in Π_m(1+k_m)^-tn. De normalisatiefactor is een functie van alle eigenwaarden in het proces. Als de som van de ladingen van positieve en negatieve k gelijk is aan 1 dan is de intensiteit van het proces gelijk aan 1 en hebben we een steady state proces gemodelleerd waarbij de intensiteit van m deelprocessen met elkaar gerelateerd zijn. Als de som van de ladingen van positieve en negatieve k niet gelijk is aan 1 dan zal de resulterende intensiteit uiteindelijk een positieve feedback zijn (exponent van e positief) of een negatieve feedback (exponent van e negatief). De grootte van de exponent zal de verdubbelingstijd of de halfwaarde tijd geven. We geven hiervan een aantal voorbeelden.

We tonen de veranderende intensiteiten van drie deelaspecten, een relatie gegeven met vierkanten, een met ruiten, en een met driehoeken op de tophoek. De resulterende relatie wordt gegeven door de datapunten met driehoeken op de basis en hiervan tonen we de getalvergelijking en het kwadraat van de determinatiecoëfficiënt R.

Dit patroon zal niet veranderen als we de logaritme nemen en het product dus vervangen door een som van logaritmen.

De normalisatie van intensiteiten inclusief referenties

De constante term (doel en anti-doel) die we eerst de waarde 0 gegeven hadden kunnen we ook door een andere getalwaarde vervangen zonder de globale karakteristieken van de relatie te veranderen. Neem bijvoorbeeld als constante term het getal 1 dan resulteert dit in de volgende tabel waarin k=0,2 en n=30:

Hier zien we terug het veelterm patroon ±(1±x) ontstaan, waarbij x nu staat voor het dubbelgetal 1±k.

Elke relatie heeft terug een duaal. Bijvoorbeeld neem 1-(1+k)ⁿ dan is zijn duaal 1+(1+k)ⁿ en op die manier kan men twee positieve feedbacks aan elkaar relateren inclusief hun referentie, wat in de volgende tabel geïllustreerd wordt:

Er geldt nu dat (1-(1+k)ⁿ)(1+(1+k)ⁿ)=(1²-(1+k)²ⁿ) en dus (1-(1+k)ⁿ)(1+(1+k)ⁿ)(1²-(1+k)²ⁿ)^-0,5=1, zodanig dat in het algemene geval voor een referentie R evengoed geldt dat (R-(1+k)ⁿ)(R+(1+k)ⁿ)(R²-(1+k)²ⁿ)^-0,5=1. Dit is andermaal niet anders dan het inzicht dat iets een eenheid zal zijn als het uitgedrukt kan worden als het (vector)product van twee andere eenheden.