De studie van welgevormde haakuitdrukkingen die leidt tot de relatie van simultaneïteit en de daaruit volgende partiële orde laat ons nu toe de tralie die opgespannen wordt door welgevormde haakuitdrukkingen ook op een grafisch zeer toegankelijke manier op te bouwen.

Twee onderscheidingen

Als voorbeeld geven we nu de tralie die opgespannen wordt door twee onderscheidingen.

We beginnen met de tabel te construeren. Er zijn hierin 2 tot de macht 2² combinaties (³2, of 2 getetreerd tot de derde) van “ja” en “neen” mogelijk.

We merken dat er vijf niveaus zijn gevormd door de aantallen “ja” en “neen” en we herschikken de tabel overeenkomstig. Die niveaus komen overeen met de verdeling van <> en <<>> in de tabel. De nummering is gekozen naar het aantal <<>> dat in de combinatie voorkomt.

Merk op dat de individuele onderscheidingen zich op het centraal niveau bevinden (hier niveau 2) samen met hun inbedding. Het centraal niveau is het enige niveau waarop zich punten en hun inbedding samen kunnen bevinden, in de tabel vinden we dan evenveel <<>> als <>. Een nieuwe onderscheiding zal altijd op het centraal niveau toegevoegd worden.

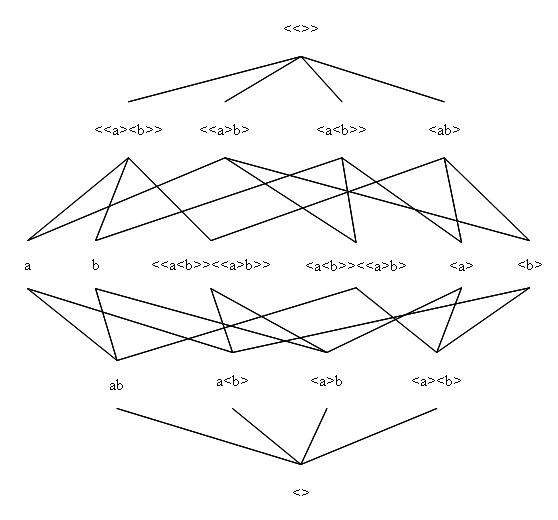
Hieronder is de tralie in twee onderscheidingen a en b grafisch weergegeven. De lijnen tussen de punten stellen de relaties van simultaneïteit voor, enkel met de onmiddellijke buren van een punt.

Deze tralie is ook voor te stellen als 4-hypercube aangezien elk punt exact vier buren heeft:

Noteer: een hypercube is de uitbreiding naar meerdere dimensies van een kubus in drie dimensies (elk hoekpunt van de kubus is met drie andere hoekpunten verbonden).

Enkele opmerkingen

Van de 16 punten hebben er slechts 2 een waarde. De andere bevinden zich hiertussen met een onbepaalde waarde. Het zijn welgevormde haakuitdrukkingen die een waarde zouden kunnen krijgen. Het zijn dus potentiële punten.

De relatie van simultaneïteit kunnen we in twee richtingen interpreteren: in de richting van de waarde <<>> (of “neen”) en in de richting van de waarde <> (of “ja”).

Indien men focust op een punt x in de tralie dan hebben we een punt tussen x en <> dat simultaan is met x een fijner punt genoemd, en we hebben een punt tussen x en <<>> waarmee x simultaan is een ruimer punt genoemd. Bijvoorbeeld: ab is fijner dan <a<b>><<a>b>, dat op zijn beurt fijner is dan <a<b>>. Omgekeerd: <a<b>> is ruimer dan <a<b>><<a>b>, dat op zijn beurt ruimer is dan ab. Grafisch is dus ook snel duidelijk dat ab fijner is dan <a<b>>.

Als oefening kan gecheckt worden dat ook formeel “een fijner punt dan x” simultaan is met x.

Voorbeeld:

Te bewijzen

<a>b is simultaan met <a<b>>, formeel: <<a<b>>><a>b heeft altijd waarde <>

Bewijs

<<a<b>>><a>b

<<a<>>><a>b

<<<>>><a>b

<<<>>><a>b

<><a>b

<>

QED

Gevolg

x is simultaan met een ruimer punt.

In elke tralie zijn er punten die onmogelijk simultaan te ervaren zijn: dit zijn onder andere de punten die de buren zijn van <<>>. We zullen deze "elkaar uitsluitende punten" noemen en we zullen zien dat ze een grote rol spelen bij veel a priori.

Voor de constructie van de volledige tralie zijn de punten <<a<b>><<a>b>> en <a<b>><<a>b> essentieel. Dit punt wordt bereikt door de operatie van transformatie en drukt nogmaals uit hoe nieuw en belangrijk deze operatie is. Wanneer deze operatie niet onderscheiden wordt, dan is het nog steeds mogelijk om een tralie te construeren met enkel meet en join. De relatie van simultaneïteit (nevenschikking) doet niet anders dan dat. Hiermee wordt dan een tralie in twee onderscheidingen gecreëerd met tussen de twee waarden drie niveaus met slechts 4 punten per niveau. Die tralie heeft dan geen 16 punten maar slechts 14.

Drie onderscheidingen

Met drie onderscheidingen zullen we dan 2 tot de macht 2³ (256) unieke combinaties van “ja” en “neen” vinden.

Uiteraard kunnen we de niveaus ook terugvinden voor drie punten. Er blijken er negen te zijn

niveau 0: <>

niveau 1: 8 punten

niveau 2: 28 punten

niveau 3: 56 punten

niveau 4: 70 punten

niveau 5: 56 punten

niveau 6: 28 punten

niveau 7: 8 punten

niveau 8: <<>>

Elk punt van deze tralie, die er grafisch al als een spinnenweb uitziet, heeft 8 buren en we zullen deze tralie dus ook als een 8-hypercube kunnen voorstellen.

Algemeen

Met n onderscheidingen zullen we dan 2 tot de macht 2ⁿ unieke combinaties van “ja” en “neen” vinden. Zij vormen een tralie waarbij elk punt 2ⁿ buren heeft. Die tralie zou dan voorgesteld kunnen worden door een 2ⁿ-hypercube.

We zullen in de tralie 2ⁿ +1 niveaus vinden en het aantal punten op één niveau zal gegeven worden door het aantal combinaties van 2ⁿ boven k, met k van 0 tot 2ⁿ, aantal dat berekend wordt door 2ⁿ!(2ⁿ-k)!^-1k!^-1. Dit zijn de bekende binomiaalcoëfficiënten.

Deze formule kunnen we als volgt begrijpen: neem 2ⁿ onderscheiden symbolen, zoals bijvoorbeeld A, B, C, D, …. Daar zijn 2ⁿ! verschillende combinaties van nevenschikking mee te maken, bijvoorbeeld ABCD…, BACD…, CADB… omdat als één symbool een positie inneemt in de nevenschikking, dan nog altijd 2ⁿ-1 mogelijkheden overblijven voor het volgende symbool enz…. We veronderstellen nu dat een aantal symbolen zich niet onderscheiden, bijvoorbeeld: A en B zijn eigenlijk van dezelfde soort, noem deze P. Nu geldt dat, als p symbolen zich niet onderscheiden en er dus p symbolen van een soort P zijn, dat dan het aantal mogelijke onderscheiden combinaties vermindert en het totaal moet gedeeld worden door p!. De 2ⁿ! verschillende combinaties worden dan gereduceerd tot 2ⁿ!p!^-1. We veronderstellen nu dat er p_i symbolen zijn die zich niet onderscheiden (en dus P_i soorten vormen) en dus wordt het aantal verschillende combinaties dan 2ⁿ!Π_ip_i!^-1. Voor twee soorten (namelijk <> en <<>> waarvan er k zijn per niveau van de ene soort en (2ⁿ-k) van de andere soort) wordt dit dan 2ⁿ!(2ⁿ-k)!^-1k!^-1.

Dit inzicht kan niet genoeg beklemtoond worden: het is het onvermijdelijke gevolg van het axioma dat de waarde “ja” een waarde “neen” impliceert en de waarde “neen” een waarde “ja” impliceert. In woorden: zeg je “ja” voor iets dan zeg je ook “neen” voor iets anders, zeg je “neen” voor iets dan zeg je ook “ja” voor iets anders.

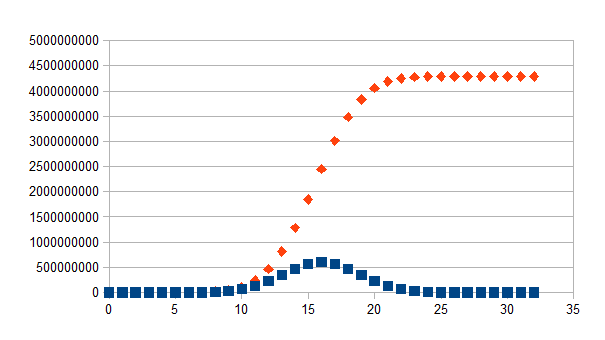
Hieronder is de frequentieverdeling en de cumulatieve distributie voor de niveaus als grafiek voorgesteld voor n=5 en dus 33 niveaus.

De meest passende Gauss curve voor twee en drie onderscheidingen (mycurvefit.com):

y = 6.069188*e^(-(x – 3)^2/(2*1.07223^2))

y = 70.52269*e^(-(x – 4)^2/(2*1.459743^2))

Eigen berekening voor drie onderscheidingen

y=941,698622*(2π*1,457446^2 )^-1e^(-(x – 4)^2/(2*1,457446^2))=70,5581992*e^(-(x – 4)^2/(2*1,457446^2))

Eigen berekening voor vijf onderscheidingen

y=30736614631,7873*(2π*2,849878^2 )^-1e^(-(x – 16)^2/(2*2,849878^2)).

Hieronder de grafiek waarbij de berekende Gauss curve (vierkanten) gecentraliseerd is op x=15 en de verdeling van de aantallen in de tralie (ruiten) gecentraliseerd is op x=16 (om de passing te kunnen demonstreren).

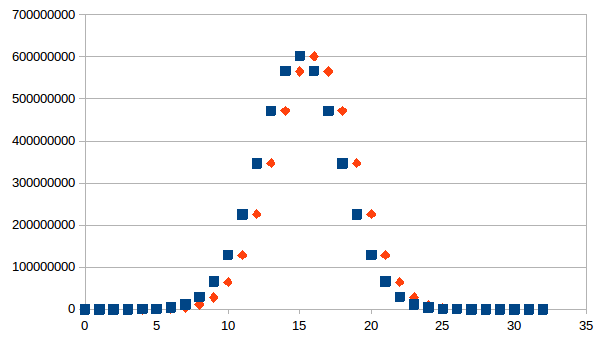
De logistische verdeling geeft zeker geen betere fit omdat de “staarten” van de verdeling in de tralie meer gelijken op de Gauss verdeling dan op de logistische verdeling.

Partiële orde

Elk punt heeft hetzelfde aantal onmiddellijk simultane buren en de relatie van simultaneïteit is een partiële orde relatie. Een onmiddellijk simultane buur van x is slechts één stap verwijderd van x. In de grafische voorstelling van de tralie is dit snel duidelijk. Behalve voor <> en <<>> zijn er zowel ruimere als fijnere onmiddellijk simultane buren. In een twee-onderscheidingen universum is het aantal onmiddellijk simultane buren 4, in een drie-onderscheidingen universum 8, in een n-onderscheidingen universum is dit 2ⁿ. Dit zijn de simultane buren we ook herkennen bij een ruimtelijke kubus, zodanig dat we de tralies als hypercubes kunnen herkennen.

Bekijken we de tralie als een netwerk dan hebben alle knooppunten (nodes) hetzelfde aantal onmiddellijke verbindingen (edges). Dat herkennen we als een eigenschap van random netwerken.

In een tralie zijn er heel wat ordeningen te vinden die ofwel monotoon fijner, ofwel monotoon ruimer zijn. Elk monotoon pad van punten die doorlopen worden heeft maar één punt op elk niveau van de tralie.

Het aantal simultane punten is een macht van 2, gegeven door het niveau van het punt. Bijvoorbeeld:

niveau 0: 1 punt

niveau 1: 2 punten

niveau 2: 4 punten

niveau 3: 8 punten

niveau 4: 16 punten

niveau 5: 32 punten

niveau 6: 64 punten

niveau 7: 128 punten

niveau 8: 256 punten

Wanneer we de logaritme van het niveau uitzetten ten opzichte van de logaritme van het aantal simultane punten van vinden we het exponentiëel verband dat hieronder weergegeven is (voor 128 niveaus en dus 7 onderscheidingen):

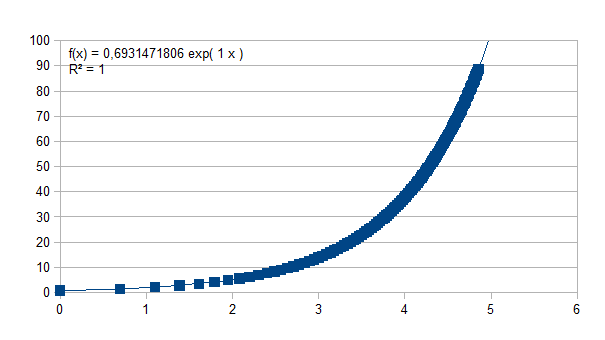
Bij de hogere niveaus is het verband nagenoeg lineair, wat we illustreren door twee voorbeelden: het interval tussen 64 en 128

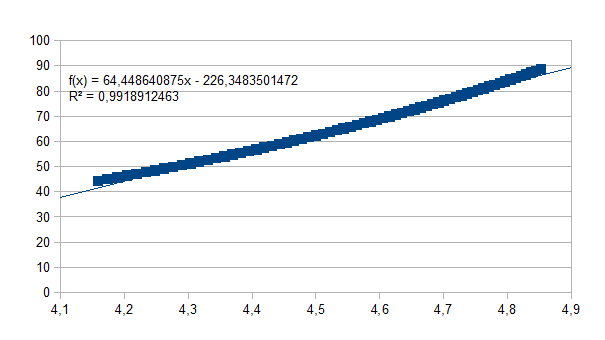
Merk op dat de determinatiecoëfficiënt nagenoeg gelijk is aan 1. Uiteraard is het exponentiëel verband exact:

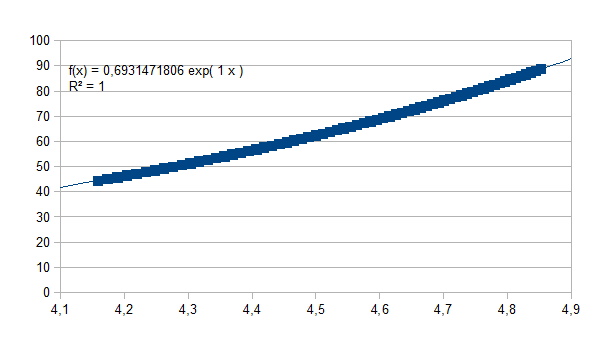
Een tweede interval nemen we tussen 128 en 256:

En uiteraard is er een exponentiëel exact verband:

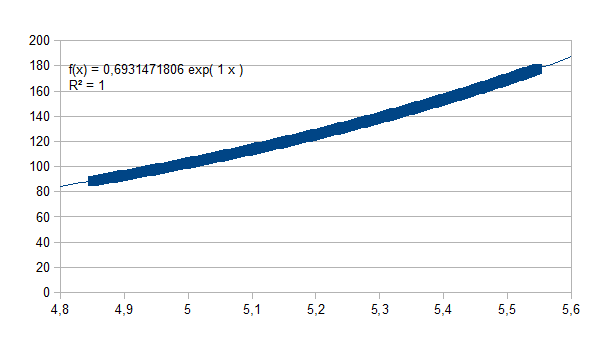
Dit betekent uiteraard dat de loglog van beide assen een verband zal geven met als helling bij elk punt de logaritme van het niveau. Dit resulteert dan in een bijna exponentiëel verband:

Onderscheidingen tralies zijn in elkaar vernest

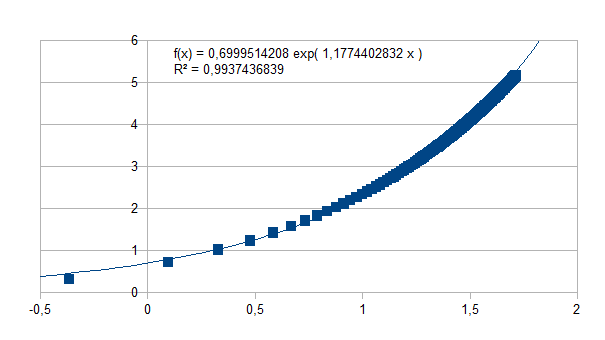
In elke tralie zitten veel tralies vernest, al deze tralies zijn gelijkvormig. Men noemt zo'n structuur een fractaal. We geven hiervan een zeer eenvoudig voorbeeld uit het drie onderscheidingen universum met één welgevormde haakuitdrukking per niveau en simultaneïteit tussen al deze punten.

Enkel de oneven niveau's hebben de drie onderscheidingen nodig, dus in deze voorstelling is a de laatst toegevoegde onderscheiding en b de voorlaatste. Elke toegevoegde onderscheiding genereert dus niveaus tussen de andere niveaus. Individuele onderscheidingen bevinden zich altijd op het centraal niveau.

Merk op dat elke onderscheiding kan staan voor een uitdrukking in een niet verder geëxpliciteerde ruimte. Bijvoorbeeld: stel dat a ↔ xy waarbij noch x noch y kunnen uitgedrukt worden in het universum waarin a uitgedrukt wordt.

Dit heeft als gevolg dat de structuur van de (n-onderscheidingen) ruimte die mee door a als combinatie van onderscheidingen gegenereerd wordt een patroon kan zijn, indien nodig, binnen een nog grotere structuur: een ruimte die opgespannen is door meer dan n onderscheidingen, waarin a staat voor een combinatie (dus welgevormde haakuitdrukking) van twee combinaties van nog niet gebruikte onderscheidingen (dus welgevormde haakuitdrukking) x en y. De ontstane structuren zijn dus zelf-gelijkvormig.

Gevolg

We kunnen zowel de waarde <> als de waarde <<>> interpreteren als een ongekend grote ruimte met een toegekende waarde zodanig dat de ruimte niet meer potentieel is. Die ruimte zal zich in grotere ruimtes bevinden en die ruimte zal kleinere ruimtes bevatten.