Enkelvoudige begrenzing

Het centraal axioma van het haakformalisme is dat er ook altijd iets anders gebeurt dan datgene waarvoor een agens kiest. Impliciet betekent dat dat het agens enkel datgene kiest waarvoor het kan kiezen. Dat betekent dus enerzijds dat een agens beperkt is, een agens kan niet gelijk wat kiezen, anderzijds dat wat gebeurt niet beperkt hoeft te zijn. De beperking hebben we op verschillende manieren gemodelleerd. Voor positieve feedback processen is dat gemodelleerd door het startpunt: het (beperkte) anti-doel van positieve feedback waarvan in de loop van de stappen het agens zich onbeperkt verder kan verwijderen. Voor negatieve feedback processen is dat gemodelleerd door het (beperkte) startpunt van negatieve feedback maar ook door het (beperkte) doel dat het agens in de loop van de stappen onbeperkt kan benaderen. Ondanks de gelijkaardige wiskundige behandeling, toch schijnen beide beperkingen kwalitatief verschillend te zijn. Er is immers een kwalitatief verschil tussen willekeurig dicht een doel benaderen vanuit een startpositie (en dus zijn start en doel een referentie) en zich willekeurig ver verwijderen van iets vanuit een startpositie (enkel de start is een referentie). Het enige gemeenschappelijke is het startpunt, voor positieve feedback start men van iets en evolueert men naar iets anders dan waar men van start (wat dat dan ook zou blijken te zijn), voor negatieve feedback start men van iets anders (wat dat dan ook zou zijn) en evolueert men naar iets, hoewel dat nooit zal bereikt worden. “Iets” en “iets anders” zijn ten opzichte van elkaar gedefinieerd en meer dan dat onderscheid hebben we niet nodig om een mogelijks heel complexe werkelijkheid te modelleren.

We hebben dus ongelimiteerde positieve of negatieve feedback gemodelleerd door deze te beschouwen als de intensiteit van een minimale entiteit (x-x₀), de “start” die gevormd wordt door de meetcontext en die als eenheid gedurende het hele proces gebruikt wordt. De beperking in de niet beperkte feedback is dus te vinden in de minimale intensiteit (x-x₀) die gevormd wordt door de meetcontext gecombineerd met de klassieke hypothese (die associativiteit, invers en dus getalverhoudingen veronderstelt). Inderdaad: enkel het samenspel van beide hypothesen leidt tot een maximale en begrensde intensiteit (x-x₀)^-1. We hebben dat geformaliseerd als “delen door nul kan niet toegelaten worden”. Als we dus, binnen die hypothese, de dynamiek gaan meten als de intensiteit van iets, dan worden we niet alleen geconfronteerd met een minimale intensiteit maar evenzeer met een maximale intensiteit. Dit betekent: x moet verschillend zijn van x₀. “Iets” is een verschil dat een verschil maakt, en dan is ook (x-x₀)^-1 gedefinieerd. (x-x₀) is begrensd en dus verschillend van nul en kan dus evenmin onbegrensd groot zijn.

De entiteit (x-x₀) is begrensd, kan niet nul zijn. De intensiteit van (x-x₀) kan onbegrensd zijn en kan ook gelijk zijn aan nul als een som gemaakt wordt van twee zelfde feedback processen, maar die evolueren in tegengestelde zin want die onbegrensdheid kan voor een samengesteld proces in twee zinnen. We geven hiervan een voorbeeld met de positieve feedback: de positieve zin, naar steeds groter, steeds meer positief en de negatieve zin, naar steeds “negatief groter”, steeds meer negatief. Merk op hoe dat onderscheid in de standaard taal moet uitgedrukt worden, positief en negatief zijn hier ten opzichte van elkaar gedefinieerd, het is moeilijk om hiervoor “groter” versus “kleiner” in de standaard taal te gebruiken. Als bij deze sommen S- of U-curves ontstaan, dan kan een gebied ontstaan rond intensiteit nul, zonder dat nul ooit bereikt wordt. De intensiteit is ook niet beperkt in de zeer kleine en zeer grote intensiteiten.

Dubbele begrenzing: de eigenwaarde als entiteit

Dat x verschillend moet zijn van x₀ is niet anders dan wat we ook verondersteld hebben bij de eigenwaarde k die we kunnen schrijven als (k-0), k moet inderdaad verschillen van nul (k=0 zou geen verandering modelleren, processnelheid nul, of afwezigheid van feedback, zowel positieve als negatieve). We hebben ook kunnen veronderstellen dat k gelijk kan zijn aan een maximum 1 (bij k=1 neemt iets dan ongelimiteerd toe waarbij we een spontane evolutie modelleren van maximale onzekerheid). Bij k=1 is er geen negatieve feedback mogelijk en dat is dus een extra voorwaarde die we niet vinden bij positieve feedback (die enkel k verschillend van nul veronderstelt). Die extra voorwaarde verklaart het verschil tussen positieve en negatieve feedback. Bij een keuze van k tussen 0 en 1 zien we dat we een aantal stappen kunnen vinden, groter dan 1 waarbij verdubbeling van (x-x₀) optreedt. Dus k heeft een rechtstreekse impact op de intensiteit van (x-x₀) die we na een aantal stappen ook als som van entiteiten kunnen interpreteren, want we bereiken 2(x-x₀) en dan 3(x-x₀) enz.... Maar als we k groter dan 1 zouden kiezen dan zouden we niet meer de evolutie van één eenheid (x-x₀) modelleren, maar er zou vanaf de eerste stap al iets meer dan één eenheid (en bij k groter dan 2 ook meerdere eenheden) kunnen ontstaan. Als k moet verschillen van nul dan zal dus (1-k) verschillen van 1 en bij een positieve k die kleiner is dan 1, dan zal (1-k) kleiner zijn dan 1. De som k+(1-k) modelleert 1 en 1 wordt ook door de verhouding kk^-1=1 gemodelleerd. Dit alles motiveert onze keuze om een eigenwaarde als dubbel begrensd te veronderstellen, conventioneel dus tussen 0 en 1. Een eigenwaarde groter dan 1 levert dan een resultaat dat niet anders is dan <<de som van een intensiteit van een eenheid, intensiteit gelijk aan een natuurlijk getal>> en <<de som van de intensiteit van een eenheid die overeenkomt met een eigenwaarde kleiner dan 1, intensiteit gelijk aan een fractie van een natuurlijk getal>>. Deze interpretatie is niet mogelijk voor een k met -1<k<0 omdat de resulterende halvering van intensiteit (dus bij een negatieve k) enkel zin heeft voor een intensiteit en niet voor een entiteit (een halve koe is geen koe meer maar een kadaver). In tegenstelling met een schaalfactor als entiteit die negatief kan zijn, moet een eigenwaarde positief zijn om de eigenwaarde als entiteit te kunnen interpreteren. We moeten dus 0<k<1 veronderstellen.

Dit is een nuttige afspraak, maar slechts een afspraak. Essentieel is dat we zowel k als (1-k) moeten beschouwen als een dubbelgetal en als verhouding die we al uitgebreid onderzocht hebben, inderdaad: stel m=2k-1 dan is de verhouding (1-k)/k niet anders dan (1-m)/(1+m). De voorwaarde 0<k<1 komt dan overeen met de voorwaarde -1<m<1. Enkel een dubbelgetal kan de rol van eenheid spelen voor gelijk welke operatie (bijvoorbeeld ook voor een machtsverheffing). We maken de keuze voor k en (1-k), maar we kunnen ook kiezen voor k en (1+k) met -1<k<0.

Een eigenwaarde k als entiteit hebben we dus al verondersteld, maar nog niet gemodelleerd. Dit gaan we nu doen door, bovenop de keuze voor k en (1-k) en 0<k<1, nog een voorwaarde te formuleren.

De interactie van processen die begrensd zijn kunnen we niet modelleren als een som (zoals we daar aantonen zijn sommen niet begrensd), maar kunnen we modelleren als een verhouding (niet verschillend van een product) waarbij de noemer niet nul kan worden. We zullen deze specifieke interactie simuleren door de evolutie van de verhouding ((1-k)(x-x₀)/(k-0)(x-x₀)) te onderzoeken met de minimale voorwaarde van een verandering van die verhouding met een fractie r bij elke stap. In deze verhouding speelt de eenheid (x-x₀) namelijk geen rol meer en dus is de verhouding (1-k)/k. Door deze verhouding te gebruiken, en 0<k<1 te veronderstellen, wordt de eenheid (x-x₀) dus “onzichtbaar” (en in het getallendomein dus gelijk aan 1). We kunnen dan veronderstellen dat k een fractie is van 1. Als k toeneemt, neemt (1-k) af, als k afneemt, neemt (1-k) toe. Hiermee demonstreren we dat deze verhouding enkel negatieve feedback kan modelleren.

We kunnen dus modelleren dat de eigenwaarde in een proces verandert tussen 0 en 1 (zonder die ooit te realiseren) op basis van een nieuwe eigenwaarde, stel r. De interpretatie daarvan is dan: r verandert simultaan (betekenis van een product) de intensiteit van de eenheid van k en de intensiteit van de (zelfde) eenheid van (1-k), de eenheid is de a priori onbekende (x-x₀)/(x-x₀) zelf die gelijk is aan 1. Het is ook dat wat we moeten besluiten uit de modellering van de klassiek analytische integratie waarbij de veranderende eenheid (x±1) blijkt te zijn, wat we nu noteren als (k±1).

Hiermee expliciteren we nog eens wat de impliciete veronderstelling is van een klassieke wiskundige techniek: enkel intensiteiten zijn betrokken, geen eenheden en als we eenheden zouden willen modelleren met verhoudingen dan is dat onmogelijk voor positieve feedback. Want verhoudingen kunnen enkel negatieve feedback modelleren, maar negatieve feedback impliceert dat een halvering mogelijk moet zijn en dat is onmogelijk voor entiteiten (eenheden, met als voorbeeld de koe) terwijl de wiskundige technieken impliciet veronderstellen dat verhoudingen altijd zinvol zijn.

De feedback processen met +r (positieve feedback dus) en -r (negatieve feedback dus) kunnen we als volgt weergeven:

Deze tabel geeft duidelijk een exponentieel verloop aan van de verhouding (1-k)/k met k een vaste waarde tussen 0 en 1. De eenheid in de tabel is dus onzichtbaar geworden (en is dus gelijk aan de onzichtbare 1 van het getallendomein).

We formuleren nu een bijkomende veronderstelling: de eenheid die gelijk is aan 1 is niet anders dan de intensiteit ((1-k)/k)(1±r)ⁿ bij stap n. Dus we veronderstellen dat dit proces de verandering tussen 0 en 1 van de eenheid zelf modelleert, eenheid die bij elke stap verandert. Bij elke stap in het proces heeft k een andere positieve waarde verschillend van nul en kleiner dan 1. Dus om evoluerende eenheid te modelleren kunnen we een variërende waarde van k bij elke stap uit de tabel, zowel voor positieve of negatieve feedback, afleiden door voor elke stap ((1-k_n)/(k_n-0))(1±r)ⁿ=1 te veronderstellen, de eenheid bij die stap die “onzichtbaar” is met de voorwaarde 0<k_n<1. We kunnen dat expliciet voorstellen door de variabele te noteren als een functie van n, dus f(n), en dit schrijven we als k_n. Dit is dan ook niets anders dan wat we doen bij een “normalisatie” bij elke stap wanneer we de interactie van positieve en negatieve feedback als een product voorstellen om te kunnen modelleren dat ze elkaar opheffen. Daar is er bij elke stap ook een andere normalisatiefactor en we hebben de normalisatie ook kunnen uitbreiden om doel en anti-doel te kunnen omvatten.

Dus de bijkomende voorwaarde is een gelijkheid, namelijk ((1-k_n)/(k_n-0))(1±r)ⁿ=1 voor elke stap. Hiermee modelleren we een analytisch model van de werkelijkheid.

Uit ((1-k_n)/(k_n-0))(1±r)ⁿ=1 leiden we het volgende af:

(1-k_n)/k_n=(1±r)^-n

-k_n=-1+k_n(1±r)^-n

k_n(1+(1±r)^-n)=1

k_n=1/(1+(1±r)^-n)

Dit is de logistische functie die de verandering geeft van k in functie van het aantal stappen in een proces. Dit geeft de evolutie van 1, de eenheid zelf, niet van de intensiteit van de eenheid. Dit is een normalisatie die het proces karakteriseert omdat het een minimaal verschil met twee getallen vastlegt: 0 en 1. Geen van de twee getallen kan een eigenwaarde zijn, het minimale verschil (infinitesimaal) karakteriseert de eenheid van het proces.

Het gevolg van deze voorwaarde is dat de eigenwaarden k_n kunnen gesommeerd worden omdat ze allemaal gelijk zijn aan de eenheid 1 en door de processtappen elkaar uitsluiten. Dit geeft het symbool Σ_nk_n betekenis, en zo we willen dank zij het infinitesimaal verschil, is dit een integraal tussen processtappen n en n+m. Dit is een cumulatie die zich onderscheidt van de cumulatie bij een constante eigenwaarde (die niet begrensd is). We kunnen dat een analytische cumulatie noemen, een cumulatie van minimale eenheden, in contrast met een cumulatie van minimale intensiteiten (van een eenheid).

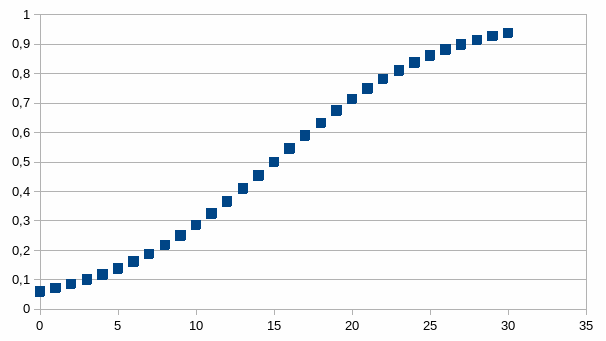
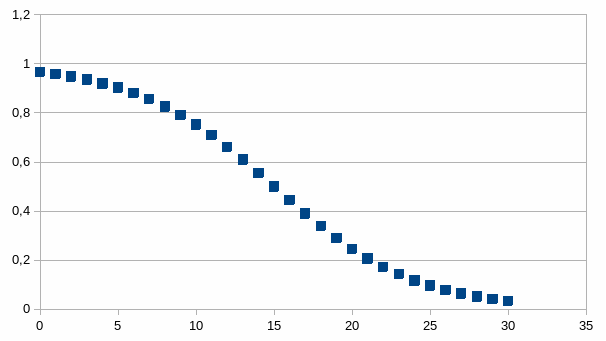
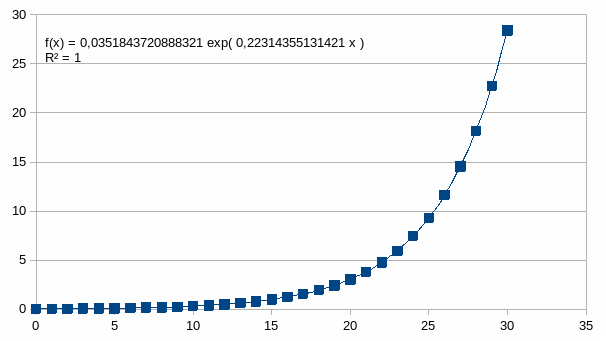
De grafiek van k_n in functie van n is een sigmoïde begrensd tussen 0 en 1. Het buigpunt van de sigmoïde is te vinden op de stap n=m, met k_n=1/(1+(1±r)^-(n-m)) want dan geldt k_n=1/2. Die sigmoïde ontstaat wanneer de verhouding van <<de intensiteit>> tot <<een verschil van de intensiteit met een doel (of anti-doel)>> een exponentieel verloop kent. Het verloop van die verhouding geven we weer in de laatste kolom met zijn vergelijking en determinatiecoëfficiënt (gelijk aan 1).

Hieronder een voorbeeld voor n tussen 0 en 30 (met het buigpunt dus op 15):

We herkennen een S-curve of Z-curve die begrensd is tussen de extrema 0 en 1. Dit verschilt fundamenteel van de S-curve die we bestudeerd hebben bij de som interactie van negatieve en positieve feedback omdat deze laatste niet begrensd is terwijl de nu onderzochte curve zowel voor lage als hoge intensiteit begrensd is. Zowel negatieve feedback als positieve feedback zijn slechts mogelijk als er een minimum verschil is bij de start en door een product (een verhouding) te gebruiken als getalfunctie is ook het andere extremum begrensd. De begrenzing modelleert de gezamenlijke eenheid in beide extrema.

Eigenwaarde als kwantum eenheid

De relatie k_n=1/(1+(1±r)^-n) genereert bij elke processtap n een eigenwaarde k_n. Dat is niet meer en niet minder dan wat we een “abrupte verandering” bij elke stap genoemd hebben, discontinu. Zoals we dat gemodelleerd hebben, bewezen we dat “de geschiedenis” van het proces in dit model geen rol hoeft te spelen, enkel het aantal stappen en de betrokken eigenwaarden. Het aantal stappen bevindt zich in de exponent en dit is de enige variabele in de relatie. Aangezien we nu begrijpen dat deze eigenwaarde de eenheid zelf is die verandert (dit in tegenstelling met een intensiteit (van een eenheid) die verandert) hebben we gemodelleerd dat entiteiten (eenheden) kunnen ontstaan en verdwijnen, “bij” een kwantum dat in de exponent duidelijk wordt, en dat we van daaruit een proces kunnen afleiden (dat dan misschien niet meer wiskundig analytisch kan gemodelleerd worden in functie van “monotoon toenemende standaard tijd” als processtap, zodanig dat dit paradoxaal lijkt op het eerste zicht). Dit proces is dan een nieuw soort klok waarbij simultaan (onafhankelijk van de tijd waarmee we de geschiedenis construeren aangezien die geen rol speelt) nieuwe entiteiten ontstaan als constituerende elementen van de klok. We kunnen ons daarom laten leiden door de inzichten van de systeem dynamica om een monotone ordening (bijvoorbeeld de tijd) in een willekeurig proces af te leiden van de processtappen en niet omgekeerd. We zullen dan simultane entiteiten kunnen modelleren, dat zijn entiteiten die ingebouwd zijn in de tralie en elkaar niet uitsluiten. Er is geen enkele reden om de standaard tijd (de atoomklok) te kiezen, met de standaard tijd kunnen we enkel elkaar uitsluitende toestanden modelleren die gemodelleerd moeten worden met een “laatst toegevoegde onderscheiding” en die toestanden kunnen we niet als entiteiten interpreteren.

We merken ook op dat het getal 1/(1+(1±r)^-n) een volwaardig dubbelgetal is in het patroon 1/(1+κ) waarin κ verschillend moet zijn van nul en verschillend van 1, dus 0<κ<1 en waarbij we konden vaststellen dat de verhouding 1/(1+k) als een som -k+k²-k³+k⁴+…-k^2m-1+k^2m benaderd kan worden.

Met aantallen in de exponent kunnen we gelijk welk geheel getal als product van priemgetallen modelleren en met priemgetallen modelleren we een tralie.

Schaalfactor voor de begrenzing

Wanneer we beide eenheden in de verhouding dezelfde intensiteit K geven dan verandert de verhouding niet, inderdaad K(1-k_n)/Kk_n=1. Het interval kunnen we verschalen door 1 te verschalen en een negatieve K geeft een begrenzing in het negatieve halfvlak vergeleken met de positieve K. Hieronder een voorbeeld met K=±5. We zien K begrensd door de waarden 0 en 5, in het eerste geval en tussen 0 en -5 in het tweede geval.

K is dus een schaalfactor voor de eenheid. Bijvoorbeeld: we kunnen K begrijpen als de onvermijdelijke intensiteit van het maximale onderscheidingen universum dat kan opgespannen worden door het agens-in-context bij het doorlopen van toestanden in een monotoon proces. De vergelijking geeft het evoluerend aantal toestanden die een toestand uitsluiten en die hier beschouwd worden als entiteiten, ze zijn dus niet het gevolg van een “laatst toegevoegde onderscheiding”. K geeft een schaal aan het universum van telbare entiteiten, een schaal die dus toelaat om entiteiten te modelleren.

Het logistisch model

De begrenzing die we gemodelleerd hebben kan ook geïnterpreteerd worden als de inherente begrenzing die verondersteld moet worden om een waarschijnlijkheid tussen 0 en 1 en een waarschijnlijkheidsverdeling zinvol te maken. We kunnen aantonen dat het logistisch model aan de hypothese van de verdeling van toestanden op hetzelfde niveau (en de hieraan impliciete veronderstelling van een spontaan proces) voldoet. In een spontaan proces neemt het aantal entiteiten (eenheden, soorten die elkaar uitsluiten) eerst toe en na het bereiken van een maximum neemt het aantal weer af. Als het proces permanente sporen achterlaat zullen de sporen op die manier verdeeld zijn. Dit model is ook het model voor de Fermi-Dirac verdeling van het aantal toestanden “op microschaal”. De Fermi-Dirac verdeling is inderdaad begrensd.

Indien de k_n begrensd zijn, zal ook de verhouding van twee verschillende k_n een logistische curve genereren, wat we illustreren in de volgende tabel.

De verhouding van (k_n+1-k_n)/(k_n+1+k_n) genereert ook een logistische curve.

Relevantie voor de fysica

De verhouding (1-k_n)/k_n is niet anders dan (½-n)/(½+n). Stel immers (½+n)=k_n. Dan is (½-n)=½-(k-½)=1-k_n. Dus (½-n)/(½+n)=(1-k_n)/k_n=(1/k_n-1). We tonen aan dat dit overeenkomt met de voorwaarde voor het bestaan van een klassiek gemiddelde en een "lokaal evenwicht" en dus voor alles wat we in de klassieke fysica kunnen anticiperen. We kunnen hiermee bijvoorbeeld de basis van de relativiteitstheorie (de Lorentz transformatie) op een nieuwe manier afleiden.

We berekenen dus de evolutie van één getal: (½-n)/(½+n)=(1-k_n)/k_n. Dat getal kwantificeert één bit en is te interpreteren als een energiedensiteit. Voor een intensiteit k_n groter dan 1 is 1/ k_n te interpreteren als een fractie van 1 en dit is dan de eenheid waaraan een intensiteit kan gegeven worden. Dit illustreert ook dat 1 en 1/k_n geen onafhankelijke eenheden zijn zoals we al opmerkten bij het onderzoek naar verhoudingen van intervallen en dus de verandering van k kan modelleren dat we de eenheid veranderen. Elk getal m kunnen we dus schrijven in het patroon (1-k_n)/k_n, inderdaad heeft de vergelijking m=(1-k_n)/ k_n één unieke oplossing voor k_n, namelijk k_n=1/(1+m). Inderdaad is een verhouding altijd mogelijk, het hoeft geen verhouding te zijn van gehele getallen (de commensurabiliteit). Het patroon (1±m)^-1 herkennen we als het basispatroon van een simultaneïteitsinterval in het getallendomein.

Besluit

We hebben al opgemerkt dat er een kwalitatief verschil is tussen willekeurig dicht een doel benaderen (gevolg van negatieve feedback) en zich willekeurig ver verwijderen van iets (gevolg van positieve feedback). We kunnen dit kwalitatief verschil nu toewijzen aan de grootte van een onderscheidingen universum dat ingezet wordt om het gedrag te modelleren. We hebben gezien dat negatieve feedback enkel mogelijk is met de intensiteit van entiteiten (die dus niet van soort veranderen en dus bestendigd blijven). Bij elke evolutie moeten we dus een verschil maken tussen twee soorten evolutie: de evolutie van een intensiteit en de evolutie van een eigenwaarde als een soort entiteit. De evolutie van een eigenwaarde kan de evolutie modelleren “in het universum van soorten”, de evolutie van de intensiteit kan de evolutie modelleren van de aantallen binnen die soorten.

Soorten ontstaan, entiteiten veranderen. Een voorbeeld van verandering is dat sommige soorten tot rijping en tot maturiteit komen waarbij dan andere processen mogelijk worden (dan pas kunnen bijvoorbeeld nakomelingen ontstaan). Processen van wasdom kunnen we herkennen aan het sigmoïdaal verloop, begrensd door een ondergrens en een bovengrens.

Entiteiten worden bestendigd door negatieve feedback processen, het onderscheidingen universum, het aantal soorten verandert dan niet. Nieuwe entiteiten kunnen ontstaan door positieve feedback en om zich dat voor te stellen is er creativiteit nodig. Het is onvermijdelijk dat zowel (1) waarnemingen nodig zijn van verschillen die de onderscheidingen leveren die die nieuwe entiteiten zouden kunnen karakteriseren als (2) constructies van nieuwe potentialiteit. Positieve feedback processen zijn een noodzakelijk voorwaarde om nieuwe entiteiten te laten ontstaan, creativiteit is een even noodzakelijke voorwaarde. Het waarnemen van nieuwe soorten begint altijd met verbeelding die dan door concrete ervaringen kan bestendigd worden. Verbeelding wordt getriggerd door te proberen waar te nemen wat je niet waarneemt. Niet waarnemen dat je niet waarneemt triggert de verbeelding niet.