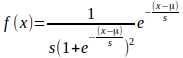We gaan nu de karakteristieken van
een proces onderzoeken waarin sommige gebeurtenissen (toestanden van
het proces) frequenter voorkomen dan andere. Toestanden zijn
welgevormde haakuitdrukkingen die
elkaar uitsluiten. De exclusieve disjunctie van twee toestanden
is
niet verschillend van de gewone disjunctie en dat is eveneens een
eigenschap van het
creatief product met een toegevoegde onderscheiding die al dan
niet ingebouwd wordt in de tralie. Dat creatief product is een
disjunctie (niet verschillend van exclusieve disjunctie) van twee
toestanden. Dank zij die laatst toegevoegde onderscheiding genereren
toestanden elkaar uitsluitende sporen in
een proces. Die sporen zullen we als resultaten van het proces
interpreteren en we spreken van de resultatenruimte
van het ervaren. Dus: als we geen idee hebben van de karakteristieken
van het proces, toch kunnen we (dank zij die sporen) een hypothese
zoeken voor het ongekend proces, want aangezien de sporen elkaar
uitsluiten zijn ze een soort en dus een entiteit die te tellen is en
is
een som te berekenen. Als we een som kunnen berekenen kunnen we
ook totalen berekenen in categorieën (of verschillende soorten) van
sporen. De (contextgebonden) waarneming van die sporen geeft dan de
mogelijkheid om de waarschijnlijkheid
te berekenen (de verhouding van niet gekozen aantallen
in een gekozen deel-soort als fractie van een
gekozen totaal-soort). Wat we tellen zijn dus
vooraf gekozen soort sporen die we zouden kunnen verbinden aan
een vooraf gekozen soort gebeurtenissen die karakteristiek
zouden zijn voor een onbekend soort proces. Dat zou dan op de
eerste plaats een proces kunnen zijn waarvan de toegevoegde
onderscheidingen niet ingebouwd worden in de bekende tralie. Indien
de laatst toegevoegde onderscheiding wel ingebouwd wordt, dan
onderscheiden we misschien nog meer soorten processen die bij
elk spoor een andere tralie genereren, maar we moeten niet sneller
willen lopen dan we kunnen.
Het is helemaal niet vanzelfsprekend om aantallen toestanden op te
tellen of te vermenigvuldigen enz… aangezien dit enkel zinvol is
voor entiteiten van dezelfde soort (bijvoorbeeld entiteiten die
dezelfde waarde hebben, waarde die verder niet gekend moet zijn).
Toestanden sluiten een referentietoestand uit, maar daarom nog niet
elkaar, tenzij
ze allemaal waarde <<>> hebben. Veronderstel immers
twee aantallen toestanden Ω(a) en Ω(b) waarvan a een
(referentie)toestand is en b een andere (referentie)toestand is. Dus
a is de disjunctie van de toestanden met aantal Ω(a) en b is de
disjunctie van de toestanden met aantal Ω(b). Dus a sluit een aantal
toestanden van een bepaalde soort (noem deze Sa) uit, en b
sluit een aantal toestanden van een bepaalde soort uit (noem deze
Sb). Als a onafhankelijk is van b dan is er voor elke a
(en dus voor elke toestand die a uitsluit) een b (en dus ook een
toestand die b uitsluit). De referentietoestanden kunnen samen
voorkomen, maar dat hoeft niet en één van de referentietoestanden
kan gekozen worden zonder dat daardoor de andere gekozen wordt. Het
totaal aantal toestanden zou dan het product Ω(a)Ω(b) zijn, maar
dat klopt enkel als alle toestanden elkaar wederzijds uitsluiten.
Veronderstel nu dat a een willekeurig referentiepunt is van
soort Sa en ook dat b een willekeurig
referentiepunt is van soort Sb, dan kan het niet anders
dan dat al deze toestanden elkaar eveneens uitsluiten want dan kiezen
we niet (er is geen criterium waarop gekozen kan worden, dat
is de essentie van “willekeur”, de enige “soort” is
“willekeurig”). Elke mogelijke conjunctie van een a van soort Sa
en een b van soort Sb heeft dan waarde <<>> en
het totaal aantal toestanden is dan het product Ω(a)Ω(b). Dit is
dan een maximum aantal. Dit is niet anders dan het inzicht dat een
soort geheel getal een priemgetal
is en dat elk geheel getal een product is van priemgetallen.
In de
kwantificering van het stappenmodel zou dan elke willekeurige
soort als <<1>> kunnen voorgesteld worden en de soort
<<1>> met het product aantal als een concatenatie.
We divergeren dan het universum.
In plaats van alle toestanden onderling te vergelijken om
afhankelijkheid te onderzoeken, kunnen we beter vergelijken per
niveau. Immers: voor een bepaald niveau kunnen de punten niet
simultaan zijn. Indien we een
relatie van simultaneïteit gevonden hebben tussen toestanden van
niveau i en niveau i+n of i-n, dan geldt dit ook voor hogere (lagere)
niveaus. Elk punt kan immers maar 2n buren hebben.
Voorbeeld: neem 00111111, dit punt heeft twee ruimere buren, namelijk
01111111 en 10111111, en zes fijnere buren, namelijk 00011111;
00101111; 00110111; 00111011; 00111101 en 00111110. Die sluiten
elkaar dus niet uit. Een punt van hetzelfde niveau kan 00111111 ofwel
uitsluiten (bijvoorbeeld 11100111) ofwel niet (bijvoorbeeld
01101111). Zoals we het uitsluiten kunnen berekenen met een
conjunctie (die dan niet verschillend is van <<>>) kunnen
we ook simultaneïteit berekenen met een conjunctie. We brengen
daartoe de beschouwde toestanden van a (noem deze Ta)
samen met de inbedding van de toestanden van b (noem deze Tb)
in hetzelfde universum en berekenen de conjunctie, dus in welgevormde
haakuitdrukking <<Ta>Tb>. Wanneer
deze niet verschillend is van <<>> dan is Tb
(de toestand ten opzichte van referentie b) fijner dan die van a
(namelijk Ta). Uiteraard moeten we ook het omgekeerde
onderzoeken en dus onderzoeken we in één beweging of
<<Ta>Tb><Ta<Tb>>
verschillend is van <<>>. Hieraan is voldaan als Ta
en Tb dezelfde waarde hebben wat die ook moge zijn,
dus ofwel beide gelijk aan <<>>, of beide gelijk aan <>.
Stel nu dat we beschikken over twee aspecten a en b die we naar
willekeur en onafhankelijk van elkaar kunnen “aanzetten” en
“uitzetten” (of die autonoom dat gedrag vertonen zonder dat we
daar enige invloed op hebben maar gedrag dat we met “ja” of
“neen” kunnen classificeren) en dat we (het spoor van) een
relatie (soort) R observeren die door die dynamiek verandert
(aanwezig is of afwezig is). “Aanzetten” is er voor kiezen dat
het aspect ervaren wordt. “Uitzetten” is er voor kiezen dat iets
anders dan het aspect ervaren wordt. Dit is het proces dat we
gedurende een tijdje laten lopen en waarvan we de sporen verzamelen.
Impliciet veronderstellen we nu dat deze herhaling mogelijk is,
dus dat er tijdens het proces geen veranderingen gebeuren in de
soorten die beïnvloed worden en die we observeren, enkel in
de intensiteit ervan. We bestuderen dus een proces in een evenwicht
situatie: er is nog wel verandering maar het is geen verandering van
het aantal relevante onderscheidingen en van de patronen die ze
vormen. In 50% van de situaties is a “aan” en onafhankelijk
daarvan is ook in 50% van de situaties b “aan”. Dit herkennen we
als pure willekeur. We kunnen nu observeren dat de relatie R (die we
gekozen hebben te observeren) helemaal niet willekeurig is (en dus
afwijkt van 50% afwezig en 50% aanwezig). Stel dat we observeren dat
in 25% van de gevallen de relatie R “aan” is, dan zouden we de
dynamiek (het verschil van de intensiteit van de waardetoekenning aan
twee toestanden in het grootste universum) kunnen afbeelden op de
mogelijke gebeurtenissen van een twee onderscheidingen universum.
Inderdaad, wat we observeren zijn (elkaar uitsluitende) toestanden en
in dat universum is de verdeling aan/uit (ja/neen) 50% voor zowel a
als voor b, en is de verdeling voor een atoom 25% “aan” versus
75% “uit”. Dit is duidelijk vanuit de
tabel van twee onderscheidingen. De relatie R blijkt dan een
relatie te zijn enkel afhankelijk van a en b, want stel dat het
percentage nog extremer zou zijn (stel 10% tegenover 90%) dan zouden
twee onderscheidingen a en b niet voldoende zijn om de relatie te
modelleren en zou het modelleren enkel in een groter universum kunnen
waarvan we dus veronderstellen dat het telkens weer gerealiseerd
wordt. Dus als we (elkaar uitsluitende) toestanden observeren dan
kunnen we zoeken in welke universa ze als toestanden optreden, enkel
op basis van hun frequentie van voorkomen (de frequentie van de
sporen die één op één gerelateerd zijn met een toestand). Dus met
het voorbeeld: in één universum 50%, in een ander universum 25% en
dit blijkt voldoende te zijn, dan is het grootste universum een twee
onderscheidingen universum. De basis hiervoor moet in het ideale
geval de volledige willekeur zijn van onafhankelijke
aspecten, ze bevinden zich in het gevonden universum op centraal
niveau. Merk op dat de waarschijnlijkheden rechtstreeks uit het
bitstring model af te leiden zijn (in twee onderscheidingen heeft een
atoom 1 bit op 4 bits die afwijkend is van de andere, dus 25%). Dus
voor dit onderzoek is het bitstring model perfect. Aangezien het
aantal atomen gelijk is aan 2n, dat ook de lengte van de
bitstring is, is er steeds een aantal onderscheidingen te vinden dat
de verdeling kan modelleren. Bijvoorbeeld 210 is 1024 en
het kleinste percentage is dan ongeveer 1 op 1000.
Merk op dat aan/uit (ja/neen) geen beperking is, dit werkt ook
voor intensiteiten, we kunnen een intensiteit altijd karakteriseren
door twee binaire beslissingen (bijvoorbeeld de eerste nemen
we als “groter of gelijk aan x” voor “aan” en “kleiner dan
x” voor “uit”, de tweede nemen we als “groter of gelijk aan
x+y” voor “aan” en “kleiner dan x+y” voor “uit” en als
alle punten elkaar uitsluiten kunnen we deels overlappende
intervallen als relaties onderscheiden die dan in een Venn
diagram voor te stellen zijn).
Een eerste stap in dit onderzoek is een catalogisering van
toestanden zodanig dat we aantallen van een bepaalde soort kunnen
herkennen en dus verzamelen. Toestanden zijn slechts toestanden ten
opzichte van elkaar en dat is onafhankelijk van een bepaald
universum. Bijvoorbeeld: <a<b>> sluit <ab> uit, of
ze nu in vier bits, in acht, in zestien… bits uitgedrukt worden. In
die zin bepaalt elke toestand een soort, namelijk de soort bepaald
door de toestanden die hijzelf uitsluit en daarenboven kan die soort
een intensiteit hebben: het aantal maal dat het bitpatroon herhaald
wordt in het grootste universum dat de evenwichtssituatie voldoende
beschrijft. Het patroon zal onveranderd zijn omdat de verhouding
aan/uit niet verandert. Bijvoorbeeld: <a<b>> vertoont de
verhouding 1/4 in twee onderscheidingen en (4 maal 1)/(4 maal 4) in
vier onderscheidingen.
De catalogisering van toestanden kunnen we dus beginnen met de
vaststelling dat twee toestanden in een lager universum ook
toestanden zijn in een hoger universum maar dan op
een dieper niveau of op een andere schaal. Dat betekent dat
toestanden zich uiteindelijk op alle niveaus kunnen bevinden. Op welk
niveau ze zich bevinden kunnen we kiezen door een andere grootte van
onderscheidingen universum. Dank zij het inzicht in simultaneïteit
zullen we een niveau interpreteren
als een soort. Een atoom is een soort en is beschikbaar vanaf één
onderscheiding, dat geldt ook voor een onderscheiding die dus ook een
soort is. Een één onderscheiding universum is het enige universum
waarop atoom en onderscheiding zich op hetzelfde niveau bevinden.
Sommige soorten zijn pas beschikbaar bij een voldoende groot
universum. Bijvoorbeeld potentiële atoomburen zijn slechts
beschikbaar vanaf twee onderscheidingen. In twee onderscheidingen
zijn 1110 (∼<<a><b>>) en 1101 (∼<a<b>>)
atomen (sluiten elkaar uit) en hun representatie in drie
onderscheidingen, namelijk 11101110 en 11011101, zijn atoomburen
in dat drie onderscheidingen universum en sluiten elkaar ook uit. En
ook: in drie onderscheidingen zijn 11111010 (∼<<a><c>>)
en 11110101 (∼<a<c>>) atoomburen die elkaar uitsluiten,
maar ze zijn opgespannen door maar twee onderscheidingen. Op alle
niveaus zullen we dus elkaar uitsluitende punten vinden. Op centraal
niveau zijn dat dan inbeddingen; dus elk punt op centraal niveau
heeft maar één ander punt dat het uitsluit op centraal niveau. Op
het hoogste (laagste) niveau is er maar 1 punt namelijk <<>>
of <>. Maar kiezen we een toestand T dan zullen we ook op alle
niveaus toestanden vinden die T uitsluiten en dat zijn soorten en ze
zijn dus te tellen in de universa waarin ze als andersduaal
gemodelleerd kunnen worden.
Verder kunnen we vaststellen dat toestanden (op hetzelfde niveau
of op verschillende niveaus) noch simultaan zijn, noch onafhankelijk
zijn van elkaar. Per niveau kan er telkens weer (bij elke
herhaling van het proces in het ervaren) maar één toestand aanwezig
zijn, immers: stel dat dit niet zo zou zijn dan zouden ze elkaar niet
uitsluiten aangezien ze gerealiseerd zouden worden door een toestand
op een hoger niveau (of zouden gebeuren simultaan met een ingebedde
toestand op een lager niveau). Aangezien we een aantal welgevormde
haakuitdrukkingen per niveau kunnen onderscheiden en sommige daarvan
toestanden zijn voor elkaar, kunnen we ook voor het maximaal aantal
toestanden in een tralie een verdeling verwachten van aantallen
tussen het centraal niveau en het extreme niveau. Als we soorten
toestanden zouden kunnen onderscheiden dan zal de soort toestand dan
gegeven worden door het niveau, en aangezien het niveau een metrische
maat is en er per niveau telkens slechts één toestand geselecteerd
wordt, dan zouden we ook de toestanden van verschillende niveaus bij
elkaar kunnen optellen. Het kan dus onmogelijk a priori duidelijk
zijn welke som in een concreet geval gemaakt werd, dit kan hooguit
achteraf vastgesteld worden.
We beschikken dan goed gedefinieerde aantallen in soorten die
opgeteld een totaal aantal toestanden van een “globale” soort
vormen. Met die verdeling kunnen we dan een waarschijnlijkheid
berekenen
van het voorkomen van een bepaald soort toestanden (en dus
van een bepaald soort mogelijk te detecteren sporen) zoals in het
hoger gegeven voorbeeld duidelijk werd waaraan we op een of andere
manier een niveau kunnen verbinden. Die soort kunnen we kiezen.
van het voorkomen van toestanden die een gekozen toestand T
uitsluiten, toestanden samengeteld voor sommige niveaus
(bijvoorbeeld
enkel even niveaus of viertallen) of alle niveaus. We weten dit
niet en we kiezen dit niet (wat natuurlijk betekent dat we het
onderscheid “niveau” niet meer hanteren en eerder een nieuwe
maat krijgen voor de grootte van het relevante onderscheidingen
universum).
We stippen daarbij ook aan dat potentiële (dus welgevormde)
haakuitdrukkingen die elkaar uitsluiten daarom nog niet elkaar
uitsluiten in een gecollapst universum of in een universum met
onvoldoende onderscheidingen om uitsluiting te kunnen uitdrukken (wat
we hierboven uitdrukten in de term “vooraf gekozen”). Toestanden
sluiten elkaar uit ten opzichte van een infimum (disjunctie): het
uitsluitingsniveau of repertorium. Gewoonlijk kiezen we <>
als infimum. De hele redenering blijft opgaan voor een
gecollapste haakuitdrukking waarbij don’t cares ontstaan en het
infimum als bijvoorbeeld 000xxxxx aangegeven zal worden, enkel drie
bits coderen hier potentiële structuur en het aantal punten dat
elkaar uitsluit zal sterk gereduceerd zijn en enkel het gevolg zijn
van de relaties tussen die drie bits.
Na dit eerste snelle inzicht bouwen we de catalogisering heel
kwantitatief op met het bitstring model van het haakformalisme en dit
vanaf een eenvoudig startpunt in drie onderscheidingen.
De verdeling van het aantal toestanden in een
tralie
Toestanden zijn relatief, ze worden gedefinieerd met behulp van
minstens een tweede punt dat ze uitsluiten. Als we één toestand
kiezen kunnen we die positioneren ten opzichte van minstens één
soort, namelijk al de punten die door de toestand uitgesloten
worden in een bepaald universum zonder dat we daarom ook die
toestanden moeten kunnen kiezen, ze zullen enkel maar gebeuren. Dat
is te tellen omdat we nooit dubbel zullen tellen. Sommige van die
niet gekozen punten (ze zijn natuurlijk niet simultaan met de gekozen
toestand) kunnen simultaan zijn met elkaar en zijn dus zeker niet van
hetzelfde niveau. Een soort kunnen we onderscheiden door de punten
verder te karakteriseren, bijvoorbeeld “van hetzelfde niveau”,
“enkel van de oneven niveaus” of “van gelijk welk niveau”.
Bijvoorbeeld: neem <<>>, dit sluit slechts één punt uit
van hetzelfde niveau, namelijk <<>>, maar sluit ook elk
ander punt uit, hoe groot het onderscheidingen universum ook gekozen
wordt en veel daarvan zijn simultaan. In drie onderscheidingen zijn
dat dus in totaal 28 punten, in n onderscheidingen zijn er
dat dus 2EXP2n. Voor <<>> kunnen we niet
kiezen, dus de waarschijnlijkheid is 0 van het realiseren van een
toestand in het geval “zelfde niveau” als in het tweede geval
“gelijk welk niveau”.
Voor een AND-atoom kunnen we wel kiezen. Neem een AND-atoom in
drie onderscheidingen, dit sluit niet elk ander punt meer uit, maar
slechts 27 (dus 28-1) andere punten (“van
gelijk welk niveau”). De waarschijnlijkheid dat een AND-atoom in
drie onderscheidingen een willekeurig ander punt uitsluit is dus
27/28=50%. Vergelijk dat met de vaststelling
dat een AND-atoom 2n-1 punten uitsluit van hetzelfde
atomair niveau in n onderscheidingen (“van hetzelfde niveau”),
punten die elkaar ook wederzijds (dus twee-aan-twee) uitsluiten en de
waarschijnlijkheid daarvan is 2-n, en voor drie
onderscheidingen is dit 1/23=12,5%. Het bitstring model
geeft ook hier de berekeningswijze aan. Dit maakt onmiddellijk
duidelijk dat de beide soorten toestanden (“van hetzelfde niveau”
versus “van gelijk welk niveau”) door hun waarschijnlijkheid van
optreden uit elkaar kunnen gehouden worden. De waarschijnlijkheid dat
een AND-atoom een willekeurig ander punt uitsluit is altijd
22expn-1/22expn=50%, onafhankelijk van het
opspannende universum. De waarschijnlijkheid dat een AND-atoom een
ander AND-atoom uitsluit is altijd 2-n en dit getal is
afhankelijk van het aantal onderscheidingen die hun universum
opspannen. Het verschil tussen de twee manieren van tellen wordt goed
geïllustreerd door het
gooien van een dobbelsteen waarbij men tot de onvermijdelijke
conclusie komt van zuivere willekeur (een waarschijnlijkheid van 50%)
in het geval men de categorieën waarin de waarnemingen moeten
ondergebracht worden niet kent, en een waarschijnlijkheid
verschillend van ½ in het geval dat men het aantal categorieën kent
(een waarschijnlijkheid van 1/n).
Een atoombuur in drie onderscheidingen sluit 26 punten
uit in drie onderscheidingen (dit is 2(8-2)) maar 212
in vier onderscheidingen (dit is 2(16-4)), waar het
uiteraard geen atoombuur meer is, en zo ook 224 in vijf
onderscheidingen (dit is 2(32-8)). We kunnen dat
veralgemenen als volgt: een willekeurig punt op niveau m sluit een
aantal punten uit in een ongekend universum met n AND-atomen, aantal
gelijk aan 2(n-m) waarbij m<n en n en m vrij te kiezen
zijn en n de lengte geeft van het bitstring model (dat ook een deel
van het universum kan representeren, namelijk het
relevante deel, als n geen macht van 2 is).
We merken dat we minstens twee soorten soorten kunnen
onderscheiden, (“van gelijk welk niveau”) versus (“van
hetzelfde niveau”). Zij hebben een soort duale verhouding tot
elkaar. We gaan nu de verdeling van toestanden in de “soort” van
beide soorten expliciteren.
Een soort van gelijk welk niveau
Het gebruik van het begrip “waarschijnlijkheid” is enkel
zinvol als een optelling leidt tot een maximum zodanig dat dit als 1
kan gekozen worden. Hieraan voldoet het totaal aantal punten in een
gekozen onderscheidingen universum maar ook het aantal atomen en het
aantal punten op hetzelfde niveau.
De waarschijnlijkheid dat <<>> een ander punt uitsluit
is 1 (in drie onderscheidingen is dit dus 28/28
of 100%, in vier onderscheidingen is dit dus 216/216
of 100%). Dus de waarschijnlijkheid dat <<>> ervaren is,
is 0.
Op het AND-atoom niveau in drie onderscheidingen zijn er 8
haakuitdrukkingen die elkaar uitsluiten. Er zijn immers 8 posities
waar één 0-bit kan gevonden worden. Dit is het enige niveau waarop
alle punten elkaar wederzijds uitsluiten. In totaal zijn er
dan 27=128 toestanden die door één punt op atomair
niveau uitgesloten worden. Die 128 toestanden hebben als
gemeenschappelijk kenmerk dat ze slechts één 1-bit
gemeenschappelijk hebben: de bit die in het AND-atoom dat ze
uitsluiten een 0-bit is. Bijvoorbeeld: neem het atoom 01111111, dit
sluit de volgende welgevormde haakuitdrukkingen uit die beginnen met
een 1-bit: 11000111, 10010000, enz…. Uiteraard zijn er simultane
punten te vinden in die 128 toestanden, bijvoorbeeld: 11100011 is
simultaan met 11000000 en beide sluiten 01111111 uit. De
waarschijnlijkheid dat een AND-atoom een ander punt uitsluit in drie
onderscheidingen is 1/2 (dus 27/28 of 50% in
drie onderscheidingen, 215/216 of 50% in vier
onderscheidingen), ofwel de helft van de punten die door <<>>
uitgesloten worden. Zuivere willekeur bevindt zich altijd op
AND-atoom niveau en aangezien we altijd iets ervaren kunnen we niet
ontsnappen aan zuivere willekeur.
We kunnen dus spreken van één toestand per niveau (die het
niveau representeert) en dan tellen hoeveel punten door die toestand
uitgesloten worden. Niveauverschillen zijn metrisch. We kunnen de
verdeling van het totaal aantal toestanden voor een punt per niveau
grafisch uitzetten voor drie onderscheidingen, het niveau op de
abscis, het aantal op de ordinaat:
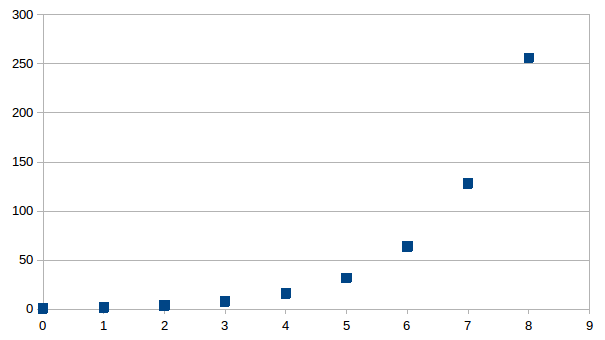
In
het grootste onderscheidingen universum dat voor ons bereikbaar is
heeft dit aantal dus een maximum. We kunnen altijd een kleiner
relevant
aantal kiezen en dus kunnen we ook een waarschijnlijkheid berekenen
in verschillende keuzen. Wat we nu ook zouden kiezen als totaal
aantal (noem dit N, het totaal aantal punten in een universum
bijvoorbeeld), het relatieve aantal van punten die uitgesloten worden
door een toestand op niveau m is 2m/N, het relatieve
aantal voor een toestand op het aanpalend niveau m+1 is 2m+1/N.
De verhouding is 2-1=50%. Dat geldt voor alle aanpalende
niveaus. De interpretatie hiervan is duidelijk: entiteiten kunnen
zich slechts op de even niveaus bevinden omdat enkel die soorten
telbaar zijn, een oneven niveau bevindt zich daar vlak naast en
modelleert gedrag. Het modelleren van willekeurig gedrag van een
entiteit is dus onvermijdelijk, het modelleren van een bepaald soort
gedrag zal een relatie zijn tussen aantallen op niet aanpalende
niveaus.
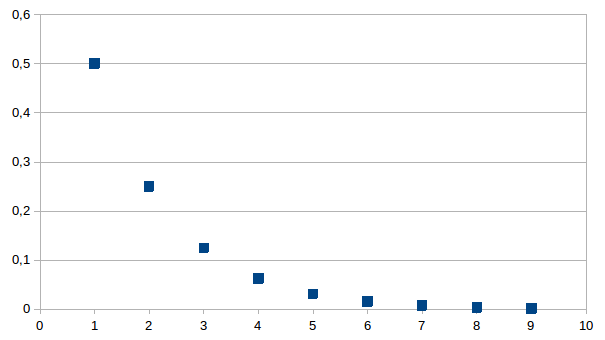
De
verdelingsfunctie (de verhouding van de aantallen in twee
opeenvolgende niveaus) is dus constant. We herkennen de verdeling als
de geometrische verdeling met p=1/2, zodanig dat
P(n)=(1-p)n-1.p=(1/2)n. Dit betekent dat, als
we de niveaus op een lijn uitzetten zoals in de bovenstaande grafiek
(en alle niveaus op gelijke afstand van elkaar aangezien
niveauverschillen metrisch zijn), dat er enkel een maximum (of
minimum) te herkennen is in de uiterste niveaus (we nummeren de
niveaus van 1 tot en met 9 en de totaliteit van de toestanden is dan
511). Veel belangrijker is het volgende inzicht: het maximum (of
minimum) is vrij te kiezen, N is vrij te kiezen, het
onderscheidingen universum is niet a priori bepaald, ook het totaal
is niet op voorhand bepaald, het totaal aantal toestanden kan
vrij gekozen worden we zijn ooit beginnen tellen en kunnen
blijven tellen). Dit betekent concreet dat, als we het aantal sporen
(toestanden) beoordelen naar het niveau waarop ze zich voordoen, dat
we altijd een niveau kunnen kiezen waarop zich dat aantal voordoet.
Er is dus een volledig vrije keuze van niveau omdat er een volledig
vrije keuze is van universum (kies een niveau, stel m, en je vind een
universum groter dan m waarbij de getelde toestanden zich op het
niveau m bevinden). De sporen die in die toestand gegenereerd worden
zijn dus relevant in alle universa en in een onderscheidingen
universum zijn de aantallen overeenkomend met m en n een macht van
twee. Een log2 transformatie van beide assen levert de volgende
grafiek op:
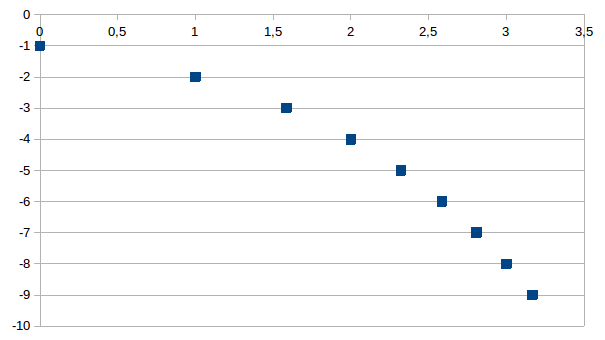
Aangezien
de toestanden elkaar uitsluiten en de niveauverschillen metrisch zijn
kunnen we de aantallen op elk niveau optellen, zo bekomen we een
geometrische reeks en aangezien de verhouding kleiner is dan 1 (in
dit geval is de verhouding ½) convergeert de reeks en dit maakt de
waarschijnlijkheid van een aantal toestanden een zinvol begrip. De
verdeling van het totaal aantal toestanden dat door een punt op een
bepaald niveau uitgesloten wordt is uiteraard enkel door het
onderscheidingen universum beperkt. De reeks 2-1+2-2+2-3+...+2-n
is (voor gelijk welke n) een benadering voor het getal 1 en
leidt tot de volgende cumulatieve distributie, die we hier
voorstellen voor een totaal aantal van 511.
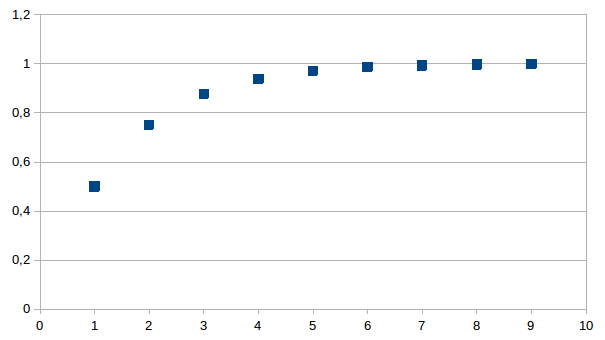
Als
we dus in staat zijn de intensiteit van een soort waar te nemen aan
mogelijke sporen kunnen we dat relateren met een vrij te kiezen
niveau in een tralie van waaruit dat aantal waargenomen wordt. Een
paar voorbeelden van zo’n sporen: de sporen gerelateerd aan de
toestanden a en <a> met disjunctie <> of aan de
toestanden <xi> en<<x>i> met
disjunctie <xi><<x>i>, of aan
de toestanden <x<h1>> en <<x><h2>>
met disjunctie <x<h1>><<x><h2>>,
waarbij dat laatste dus een algemeen voorbeeld is voor gelijk welke
1-splitsing.
Op die basis kunnen de toestanden nog verder gecatalogiseerd worden:
andersduale
en de rest. De andersduale kunnen, dank zij de inbeddingssymmetrie,
geteld worden en coderen dus impliciet voor een aantal, de andere
niet. De andersduale kunnen enkel op even niveaus voorkomen en het
aantal andersdualen is exact het aantal punten op eenzelfde niveau in
een universum met één onderscheiding minder.
Een soort van hetzelfde niveau
Op het uiterste niveau is er 1 welgevormde haakuitdrukkingen en
het sluit zichzelf uit (als <<>>) of in (als <>),
correcter maar abstracter: het is niet te onderscheiden van zichzelf.
We volgen de redenering met laagbits en hoogbits maar exact
dezelfde redenering is mogelijk voor het geval de posities niet
betekend of don’t care zouden zijn.
Op het AND-atoom niveau in drie onderscheidingen zijn er 8
haakuitdrukkingen die elkaar uitsluiten. Er zijn immers 8 posities
waar één 0-bit kan gevonden worden. Het aantal is dus 8!/1!7!. Dit
is het enige niveau waarop alle punten elkaar wederzijds
uitsluiten. Elkaar wederzijds uitsluiten is onvermijdelijk, wat we
formeel terugvinden als het infimum van deze 8 welgevormde
haakuitdrukkingen: het infimum is <>.
Er zijn 28 atoomburen in drie onderscheidingen en dat zijn de
bitstrings met 2 laagbits (0) en 6 hoogbits (1). Voor elke positie
zijn er 7 (namelijk 7!/1!6!) varianten met een 0 op die positie. Een
atoombuur die de variant met een 0 op een bepaalde positie uitsluit,
moet dus een 1 hebben op die positie en dat is dus exact hetzelfde
aantal. Er blijven nog 28-7=21 bitstrings over met op die positie een
1. Van die 21 zijn er 6 (6!/1!5!) met de 0 op een andere positie en
die worden uitgesloten door een even groot aantal met 1 op die
positie. Blijven over: 21-6=15 kandidaten en dit is 6!/2!4!. Dus dit
is het aantal welgevormde haakuitdrukkingen op datzelfde niveau (twee
0-bits, zes 1-bits) die een willekeurig punt op dat niveau
uitsluiten. Voorbeeld: neem 00111111, dit punt sluit de volgende 15
uit op hetzelfde niveau: 11001111; 11010111; 11011011; 11011101;
11011110; 11100111;
11101011; 11101101; 11101110; 11110011; 11110101; 11110110; 11111001;
11111010; 11111100. Aangezien dit een even niveau is zijn er
andersduale
punten te vinden. Er zijn er maar twee die ook 00111111 uitsluiten,
zij zijn 11011011 en 11100111. We
vinden die andersduale punten door een splitsing uit te voeren naar
een universum met 1 onderscheiding minder.
De disjunctie van de 15 punten die
00111111 uitsluiten is 11000000. Beide punten sluiten elkaar uit. De
disjunctie van de andersduale punten 11011011 en 11100111 is 11000011
en dit is een andersduaal punt op centraal niveau.
Elk van de punten op dit niveau wordt gerealiseerd door 2 ruimste
(atomaire) toestanden. Aangezien atomaire toestanden elkaar
wederzijds uitsluiten kunnen we het getal 2 gebruiken om het niveau
te karakteriseren. Een toestand op het niveau onder het atomaire
wordt ofwel door het ene atoom, ofwel door het andere atoom
gerealiseerd. Elke atomaire toestand realiseert 5 van deze punten op
dat niveau. Dat zijn er 5!/1!4!=5. Waarom? 6-1=5 (één toestand is
gekozen) en er blijft nog één 0-bit over. Het andersduaal punt
11011011 staat
voor <a<b>c><<a>b<c>> en dit drukt
uit dat a en c dezelfde waarde hebben en b de tegengestelde waarde.
Het andersduaal punt 11100111 staat voor <ab<c>><<a><b>c>
en dit drukt uit dat a en b dezelfde waarde hebben en c de
tegengestelde waarde. Het andersduaal punt 11000011 staat voor
<b<c>><<b>c> of dus b•c, of b en c hebben
tegengestelde waarde (en deze relatie is onafhankelijk van de waarde
van a). Het is een punt op centraal niveau, waar zich ook zijn
inbedding bevindt, namelijk <b•c>.
Noteer: In het eerste geval (een soort
van gelijk welk niveau) hebben we het totaal aantal punten gezocht
met een eenvoudige redenering. Dit is volledig compatibel met de
redenering die enkel naar de niveaus kijkt. Het totaal aantal
punten die 00111111 uitsluit is immers de som van de punten op de
verschillende niveaus dus
6!/0!6!+6!/1!5!+6!/2!4!+6!/3!3!+6!/4!2!+6!/5!1!+6!/6!0!=1+6+15+20+15+6+1=64.
Vier voorbeelden van zo’n punten zijn: 11111111; 11111101;
11010011; 11000000 en het is duidelijk dat sommige (zoals 11111101 en
11000000) simultaan zijn. Die punten worden door een verschillend
aantal atomaire toestanden gerealiseerd, bijvoorbeeld 11010011 (die
00111111 uitsluit) wordt gerealiseerd door drie atomaire toestanden
11011111; 11110111; 11111011. In totaal zijn er dan 26=64
toestanden die door één punt op dat niveau uitgesloten worden en
deze redenering hebben we gevolgd in het eerste geval.
We herhalen deze opbouw voor de 56 punten met drie nullen in drie
onderscheidingen. Voor de 0 op de meest linkse positie zijn er 21
(7!/2!5!) die die 0 hebben. Er blijven nog 35 kandidaten over. Van
die 35 zijn er 15 (6!/2!4!) met de 0 op de tweede positie. Er blijven
20 over. Daarvan zijn er nog 10 (5!/2!3!) met de 0 op de derde
positie. Er blijven 10 over en dit is 5!/3!2! Bijvoorbeeld neem
00011111 en dit punt sluit uit: 11100011; 11100101; 11100110;
11101001; 11101010; 11101100; 11110001; 11110010; 11110100; 11111000.
Op dit niveau zijn er dus 10 punten die een gekozen punt uitsluiten.
Aangezien dit een oneven niveau is zijn er geen andersduale punten te
vinden. Er zijn voor elke toestand drie atomaire toestanden die
elkaar uitsluiten, wat betekent dat een punt op dat niveau ofwel door
de eerste, ofwel door de tweede, ofwel door de derde atomaire
toestand gerealiseerd wordt. Elke atomair toestand realiseert 6 van
deze uitsluitende punten, dat zijn er 4 twee aan twee 4!/2!2!=6.
Waarom? 5-1=4 (één toestand is gekozen) en er blijven nog twee
0-bits over.
In totaal zijn er dan 25=32
toestanden die door één punt op dat niveau uitgesloten worden, en
uiteraard zullen ook bij die 32 toestanden toestanden vinden die
onderling simultaan zijn (zoals bijvoorbeeld 11101001 en 11100001),
en dit hebben we reeds in het eerste geval vastgesteld.
Op centraal niveau (met 70 punten) is er voor elk punt maar één
uitsluitende toestand meer, een volledig gelijkaardige situatie als
bij het uiterste niveau. Dit aantal is 4!/4!0!. Voor elk punt zijn er
4 atomaire toestanden en elke atomaire toestand realiseert dit enige
punt. Waarom? 4-1=3 en er blijven nog 3 0-bits over dus 3!/3!0!=1. De
andersduale punten op dit niveau zijn 00111100, 01011010, 01100110 en
hun inbeddingen 11000011, 10100101, 10011001. Het zijn er zes omdat
dit het aantal punten is in twee onderscheidingen op centraal niveau.
In totaal zijn er dan 24=16 toestanden die door één punt
op dat niveau uitgesloten worden, bijvoorbeeld: 11110000 sluit
11101111, 10001111 enz... uit.
Op het niveau onder het centraal niveau zijn er geen punten meer
die toestanden van hetzelfde niveau kunnen zijn. Maar zo één punt
op dat niveau zal wel 23=8 toestanden uitsluiten. Met een
concreet voorbeeld: 00000111 sluit uit: 11111000, 11111001, 11111011,
enz… tot de drie beschikbare bits allemaal in al hun combinaties
gebruikt werden.
De volgende niveaus vertonen natuurlijk een gelijkaardige
eigenschap dat er geen punten meer zijn die toestanden van hetzelfde
niveau kunnen zijn, en het totaal aantal dat één punt uitsluit is
dan 22 respectievelijk 21 en 20.
We kunnen de verdeling van het totaal aantal toestanden per niveau
(toestanden enkel van een bepaald niveau of soort) voor drie
onderscheidingen grafisch voorstellen als volgt:
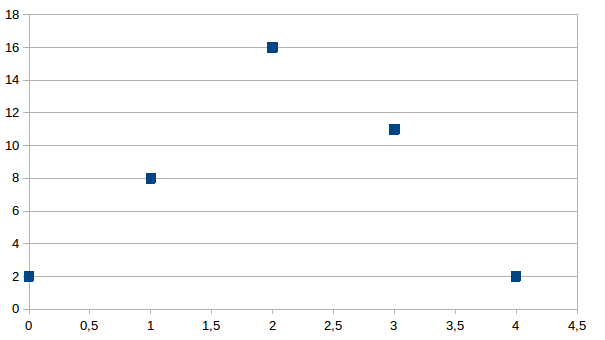
Voor
alle verdere soorten is het aantal gelijk aan nul.
Deze verdeling is geen constante zoals in het eerst bestudeerde
geval, heeft een maximum op een bepaald niveau tussen het uiterste en
het centraal niveau en is in maximum en minimum begrensd door de
vrije keuze van een onderscheidingen universum.
Dit leidt tot de volgende cumulatieve distributie:
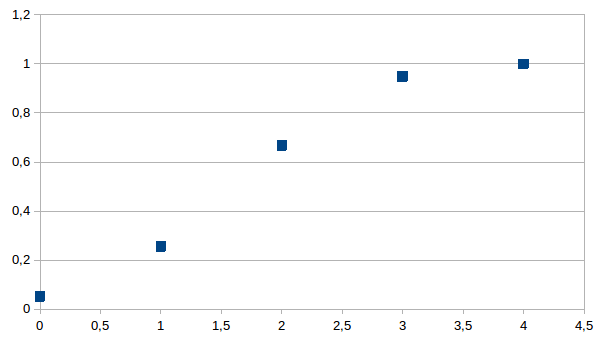
De
verdeling die zo ontstaat is veeleer een logistische dan een normale
(Gauss) verdeling wat we demonstreren door de beste passing te zoeken
in een universum van zes onderscheidingen.
We geven eerst de best passende Gauss verdeling (vierkanten,
gemiddelde waarde 17,60445613, spreiding 2,876262812,
normalisatiefactor 1,34364.1014) ten opzichte van de
verdeling van toestanden per niveau (ruiten).
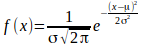

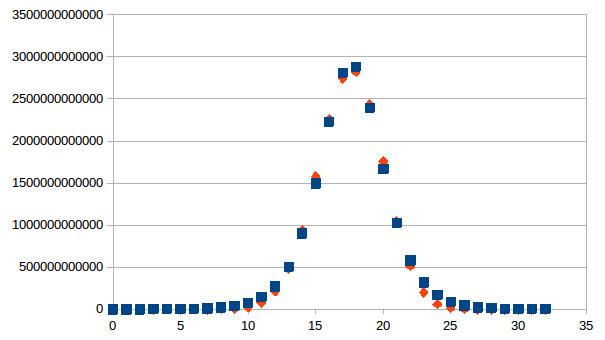
De
logistische verdeling met gemiddelde 17,619101, spreiding 1,513849 en
normalisatiefactor 1,77.1013 (vierkanten) past beter bij
de verdeling van toestanden per niveau (ruiten).
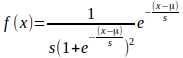
Bespreking
De logistische verdeling is de verdeling die ontstaat als
positieve en negatieve feedback begrensd
zijn door de verhouding van een maximum tot een minimum als
eenheid waarvan de intensiteit een exponentieel verloop kent en op
dat verloop genormaliseerd wordt.
De geometrische verdeling en de logistische verdeling zijn
onvermijdelijk aan elkaar gerelateerd. Kiezen we het niveau (de
soort) van een beperkt aantal afhankelijke uitgesloten
aspecten of toestanden dan is er geen vrije keuze meer voor het
niveau van het totaal aantal uitgesloten aspecten of
toestanden omdat het onderscheidingen universum door die eerste keuze
vastgelegd werd. En ook: kiezen we het niveau (de soort) van het
totaal aantal uitgesloten aspecten of toestanden dan is er
geen vrije keuze meer voor het beperkt aantal afhankelijke
uitgesloten aspecten of toestanden per niveau omdat het
onderscheidingen universum door die eerste keuze vastgelegd werd.
In elke tralie kunnen we drie soorten welgevormde
haakuitdrukkingen onderscheiden: zelfduale, andersduale en logische
relaties van beide. De zelfduale kunnen zich enkel op centraal
niveau bevinden, en dat is zo, hoe groot het universum ook zou zijn.
De andersduale kunnen zich enkel op de even niveaus bevinden,
onder andere ook op centraal niveau, en de logische relaties kunnen
zich op elk niveau bevinden, en voor beide laatste geldt: hoe
groter het universum, hoe meer mogelijkheden.
Dus als het aantal toestanden op meerdere niveaus samengeteld
wordt dan zal zich dat uiten in een verdeling die een combinatie van
beide extremen zal zijn. Dit is niet a priori gegeven en het
resultaat kan aanleiding geven tot een mogelijke kandidaat voor een
universum en een zoektocht naar meer relevante onderscheidingen.