Een Venn diagram is een zeer gekend en didactisch instrument om relaties tussen deelverzamelingen weer te geven. Nochtans sluipen in dit model (deze voorstelling) vooronderstellingen over deelverzamelingen binnen die in het haakformalisme niet noodzakelijk moeten gemaakt worden en dus met het haakformalisme kunnen geëxpliciteerd worden.

De vooronderstelling is dat alle elementen van de verzameling dezelfde waarde hebben, de elementen zijn dus telbaar. Zo’n verzameling hebben we genoteerd als {x_n, <x_n><<x>_n>}. De verschilverzameling van <x_n><<x>_n> blijkt dan <<<x>_n><x_n>> te zijn, dit is niet anders dan de inbedding van de specificatie van de verzameling. Dus als we <x_n><<x>_n> noteren als a, dan zal de verschilverzameling kunnen genoteerd worden als <a> en met beide elementen kunnen we een één onderscheiding universum opbouwen. Op dezelfde manier kunnen we dan uitbreiden naar meerdere onderscheidingen met bijvoorbeeld een <x_m><<x>_m> enz....

Dat alle elementen dezelfde waarde hebben kunnen we illustreren wanneer we daarenboven veronderstellen dat alle elementen elkaar uitsluiten, ze hebben dus allemaal waarde <<>> en zo veronderstellen we dat de som gegeven wordt door een disjunctie (in het duale geval zou de som gegeven worden door een conjunctie). Elke deelverzameling heeft als zodanig ook een infimum en het fijnste infimum kunnen we voorstellen door n=2 te nemen (het kleinste aantal onderscheidingen waarvan we kunnen zeggen dat ze dezelfde waarde hebben). We merken nu op dat we in het algemeen twee soorten deelverzamelingen hebben moeten onderscheiden, x_n versus <<x>_n>. De relaties van deelverzamelingen met elkaar kunnen we in hun algemeenheid bestuderen (met x_i en <<x>_i> versus x_j en <<x>_j>) zodanig dat we ook moeten vaststellen dat in het model van een Venn diagram een bijkomende veronderstelling gemaakt wordt door zowel een supremum als een infimum te veronderstellen voor elke deelverzameling. Er is dan ook een bovengrens aan te nemen voor het aantal elementen die men wil beschouwen. Elke deelverzameling krijgt hierdoor dan ook een supremum indien de elementen elkaar uitsluiten, en een infimum indien de elementen elkaar insluiten en het is zinvol om te spreken van de inbedding van een deelverzameling, namelijk alle elementen die geen element zijn van de deelverzameling.

Basis tralie

We hebben nu alle noodzakelijke veronderstellingen gemaakt om conjuncties en disjuncties te berekenen van verschillende deelverzamelingen en daarmee een tralie op te bouwen. Voor twee deelverzamelingen (impliciet dus van een grotere omvattende verzameling) krijgen we een tralie die isomorf is met het twee onderscheidingen universum. Hieronder de vertaling, niveau per niveau in vier verschillende noteringen.

Niveau 4

Niveau 3

Niveau 2

Niveau 1

Niveau 0

We merken nu het volgende patroon op: de 16 mogelijke diagrammen (deelverzamelingen) van het patroon dat door twee deelverzamelingen a en b gegenereerd worden, zijn op te splitsen in

• 8 deelverzamelingen die kunnen aangeduid en dus bestudeerd worden zonder de omvattende context van minimaal 16 deelverzamelingen maar mogelijks nog meer

• 8 deelverzamelingen die kunnen aangeduid en dus bestudeerd worden als hun duaal, dat we ook als complement ten opzichte van de eerste kunnen beschouwen. Het begrip “duaal” kunnen we altijd gebruiken. Als we het begrip “complement” gebruiken verwijzen we dan impliciet naar de 16 deelverzamelingen. Dit maakt dan nog eens de vooronderstelling van het model van complement duidelijk: de context is begrensd en gekend.

Die deelverzamelingen komen overeen met alle bitstrings waar bijvoorbeeld de meest linkse bit in het eerste geval positief is en in het tweede geval waar de meest linkse bit negatief is, of met andere woorden gezegd: waarbij de disjunctie ab niet kan onderscheiden worden van het ervaren zelf.

14 gehelen

De verdeling van een geheel in blokken waarvan de elementen allemaal dezelfde waarde hebben en waarvan de unie van de blokken het geheel vormt wordt een partitie genoemd. Een partitie heeft uiteraard een duaal en we kunnen dat illustreren door de tralies voor één van de gehelen expliciet te construeren. In twee onderscheidingen heeft één geheel drie partities: neem bijvoorbeeld het punt <<a><b>>, dus (+++-) en op het volgende niveau is het punt (+--+) te vinden dat het eerste punt uitsluit en insluit (de conjunctie is het supremum <<>>, de disjunctie is het infimum ab).

ab

De tralie die dan ontstaat herkennen we natuurlijk en we kunnen controleren dat, als zowel a als b de waarde <<>> hebben, dan de 8 punten de waarde <<>> hebben.

Niveau 4

Niveau 3

Niveau 2

Niveau 1

<ab>

De duale tralie wordt dan gegeven door het supremum <ab>, op het volgende niveau <a>, <b>, <<a<b>><<a>b>>, op het niveau daaronder komen <a><b>, <a>b en a<b>, op het niveau daaronder staat <> en dat is het infimum. En dus: als ab waarde <<>> heeft, dan heeft <ab> waarde <>. In dit geval zou je kunnen zeggen dat je kijkt naar punten die elkaar "insluiten", allemaal waarde <> hebben, het duale van het eerste geval. Het abstracte diagram dat de duale tralie kan voorstellen is exact hetzelfde diagram.

Niveau 3

Niveau 2

Niveau 1

Niveau 0

Grafisch kunnen we beide tralies als volgt voorstellen als twee kubussen in drie dimensies die samen een 4-hypercube vormen:

Venn diagram

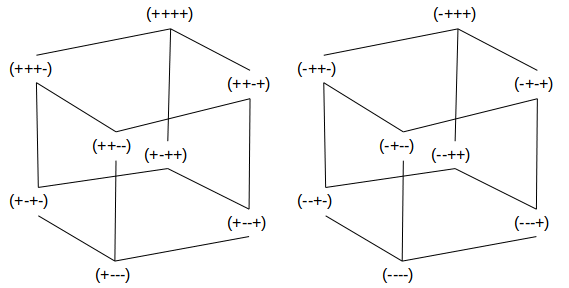
We illustreren nu hoe met een ervaren ab een Venn diagram gemaakt wordt.

De tralie wordt volledig opgespannen door de 3=(2²-1) AND-atomen die de disjunctie ab realiseren (duaal door de 3 OR-atomen <a><b>, <a>b en a<b>), wat we in diagram vorm als volgt kunnen demonstreren:

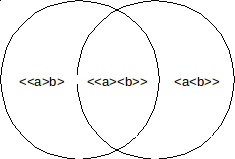
De andere deelverzamelingen (dus a, b, <a<b>><<a>b>, ab) kunnen als som (disjunctie niet verschillend van exclusieve disjunctie) van deze drie deelverzamelingen geconstrueerd worden.

Dit is de tralie waarbij de meest linkse bit irrelevant is en dus kan vervangen worden door een don’t care. Het patroon is dus (x...) en het is het patroon dat belangrijk is. Het patroon kan gerealiseerd worden als (x---) of als (x+++) met alle mogelijkheden daartussen. De som van (+++-), (++-+) en (+-++) is niet verschillend van de som van (x++-), (x+-+) en (x-++).

We herkennen dat we deze tralie bestudeerd hebben bij de rekenmethodes die gebruikt worden voor waarschijnlijkheden, wat ons nu in staat stelt om deze Venn diagrammen als volgt te interpreteren.

Elke deelverzameling is “een gebied” van elkaar uitsluitende punten. Die punten kunnen afgebeeld worden op toestanden aangezien toestanden elkaar uitsluiten, en daartoe is nodig en voldoende om alle onderscheidingen die een toestand opspannen te kennen. Aangezien in dit geval alle toestanden dezelfde waarde hebben, namelijk <<>>, kunnen we ze tellen en de disjunctie van toestanden is dezelfde deelverzameling als de exclusieve disjunctie van toestanden. De toestanden die voorgesteld worden als de punten in een bepaald gebied zijn de toestanden waarin een deelverzameling zich kan bevinden. Als we zouden willen om die toestanden uniek te coderen dan zouden we veel meer onderscheidingen nodig hebben dan de paar onderscheidingen die het diagram opspannen. Het aantal toestanden is beperkt en het wordt in dit model gegeven door de grootte van het gebied. Dat getal gedeeld door het totaal aantal toestanden in het grootste gebied is de waarschijnlijkheid dat de deelverzameling zich in een bepaalde toestand bevindt. We kunnen dus rekenen met deze gebieden zoals we kunnen rekenen met waarschijnlijkheden. De deelverzamelingen die kunnen onderscheiden worden zijn voor elk diagram beperkt en vormen dus een uniek patroon dat onafhankelijk is van de grootte van de deelverzameling (hetzelfde diagram, met dezelfde overlappingen, kan men dus tekenen met verschillende grootten van deelgebieden, dus het gebied a en het gebied b vormen een patroon dat enkel bepaald wordt door de veronderstelling dat ze al dan niet overlappen, we herkennen hierin dat we altijd in staat zijn, in een potentieel zeer grote tralie, deeltralies te onderscheiden, waarbij we dus niet alle onderscheidingen van de grote tralie nodig hebben). De grootte karakteriseert de deelverzameling niet, de deelverzameling wordt gekarakteriseerd door het patroon van alle onderscheidbare deelverzamelingen in een bepaald diagram. Dat bedoelt men als men spreekt over multisets.

De grootte kunnen we dus aangeven als de getalfunctie P(E) van de waarschijnlijkheidsrekening. We merken nu op dat in het algemeen geldt dat de conjunctie van a en b gegeven is door <<a><b>>, dus <>⊕<a>⊕<b>⊕a•b, en de disjunctie van a en b is ab, dus <<>>⊕<a>⊕<b>⊕<a•b>. De som van beide is a⊕b. Dit geldt voor zowel een niet-gecollapste tralie als voor een gecollapste tralie (wat te bewijzen is met de binaire berekeningen voor gecollapste haakuitdrukkingen). Voor de grootte geldt dan P(<<a><b>>)+P(ab)=P(a)+P(b) en dat is niet anders dan een van de axioma’s van de waarschijnlijkheidsrekening, namelijk P(E₁∪E₂)=P(E₁)+P(E₂) dan en slechts dan wanneer E₁∩E₂=∅, en dus P(<<a><b>>)=0.

In een Venn diagram kunnen we dus ook spreken van een complement. Namelijk de som van de intensiteiten van <<a>b>, <<a><b>>,<a<b>> is niet verschillend van de intensiteit van ab en dus, bijvoorbeeld, is de intensiteit van <a<b>> het complement van de intensiteit van de eenheid "<<a>b>+<<a><b>>", en deze laatste som is niet anders dan de intensiteit van a.

Essentieel aan de mogelijke patronen is dat sommige punten in verschillende deelverzamelingen gemeenschappelijk zijn (de punten van hun doorsnede), dit betekent in deze interpretatie dat sommige deelverzamelingen zich in dezelfde toestand kunnen bevinden. Dus als we naar een Venn diagram kijken dan kijken we naar een patroon van overlappingen (doorsneden), gegeven een bepaalde unie van elkaar uitsluitende punten. De hoeveelheid punten is onafhankelijk van het patroon van de structuur die door de overlappingen voorgesteld wordt. Alle mogelijke deelverzamelingen worden opgespannen door een zeer beperkt aantal “grond-gebieden” die dan overeenkomen met de onderscheidingen in het haakformalisme.

Als x en y elkaar uitsluiten (dus in de collaps dat <<x><y>> waarde <<>> heeft) dan zijn de opspannende grond-gebieden niet anders dan x, y en <x<y>><<x>y>.

We kunnen deze tralie daarbij ook afbeelden in het drie onderscheidingen universum met een laatst toegevoegde onderscheiding. De cirkelvormige gebieden zijn dan de disjuncties <u<w>><vw> (links) en <vw><<u<w>><vw>> die niet anders is dan u<w> (rechts).

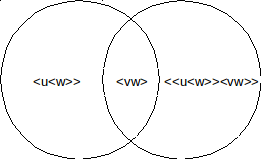
Uiteraard kan het voorbeeld dat we gegeven hebben met twee onderscheidingen verder uitgebreid worden. We documenteren dat met een Venn diagram met drie opspannende deelverzamelingen a, b en c en 7=(2³-1) AND-atomen. Hier zien we dus de ervaren disjunctie abc met zijn binaire representatie (x-------). Ook hier zijn alle andere deelverzamelingen door sommen te construeren aangezien de 7 AND-atomen elkaar uitsluiten.

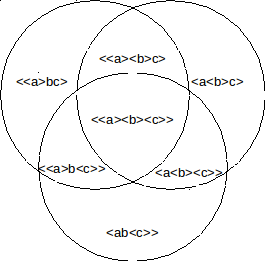
Het totaal aantal toestanden dat in dit diagram voorgesteld wordt is de som van de intensiteiten van de 7 gebieden. De toestanden die <<a>bc>, <a<b>c>, <ab<c>> realiseren, realiseren slechts 1 onderscheiding. De toestanden die <a<b><c>>, <<a>b<c>>, <<a><b>c> realiseren, realiseren 2 onderscheidingen. De toestanden die <<a><b><c>> realiseren, realiseren 3 onderscheidingen. Dat patroon zal zich ook voor alle hogere universa manifesteren en de toestanden die <<x>_iy_j> realiseren zullen i onderscheidingen realiseren waarbij i+j=n, met n het totaal aantal onderscheidingen. Merk op dat j=0 kan genomen worden, maar niet i=0. Worden de functies van i en j gewisseld (dus i=0 kan maar niet j=0), dan wisselt men naar het complement ten opzichte van het aantal toestanden van de context. Het getal i codeert dus structuur: het aantal onderscheidingen dat door een toestand, die enkel maar kan gebeuren, gerealiseerd wordt.