Elke welgevormde haakuitdrukking h kan geschreven worden als (h⊗h)_ℵ en dit betekent dat ℵ in (h⊗h)_ℵ kan geïnterpreteerd worden als het aantal maal dat de bitstring van h moet herhaald worden om h in het meest geschikte universum uit te drukken. We herkennen dat aan de concatenatie van de bitstrings die we hier aanduiden als h.h met het typografisch punt als verbinding. Het onderscheidingen universum met de bitstring h.h heeft dan 1 onderscheiding meer dan het onderscheidingen universum van h. Als het aantal onderscheidingen groter moet worden dan moeten we het onderscheidingen universum divergeren. Als het aantal onderscheidingen kleiner kan worden dan kunnen we het onderscheidingen universum convergeren. Deze concatenatie voegt dus een onderscheiding bij. We herkennen dit heel duidelijk met een voorbeeld.

Neem als h₁ in het twee onderscheidingen universum b dus in bitstring 1100, neem als h₂ in het twee onderscheidingen universum <ab> dus in bitstring 0111. Vorm nu de concatenatie h₁.h₂ 1100.0111. Dit is niet anders dan <c<b>><<c>ab>, of als creatief product (b⊗<ab>)_c. Vorm nu de concatenatie h₂.h₁ 0111.1100. Dit is niet anders dan <cab><<c><b>>, of als creatief product (<ab>⊗b)_c. We hebben twee elkaar uitsluitende bitstrings gekozen en het gevolg is dat de creatieve producten elkaar ook uitsluiten.

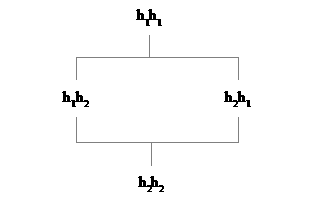
We kunnen nu twee haakuitdrukkingen veronderstellen waartussen een simultaneïteitsrelatie bestaat, veronderstel dat h₂ fijner is dan h₁, bijvoorbeeld neem als h₁ 1100 en als h₂ 1000. Dit zal altijd aanleiding geven tot het verschijnen van tussenliggende niveaus die enkel in het hogere universum kunnen uitgedrukt worden en dus deeltralies met het volgende patroon:

Met voorbeeld komt h₁.h₂ overeen met 1100.1000 en h₂.h₁ komt overeen met 1000.1100.

Dit kunnen we een divergentie-splitsing noemen en als c de laatst toegevoegde onderscheiding is dan zijn ze elkaars invers ten opzichte van de extrema. Inderdaad hebben we in het algemeen aangetoond dat het creatief product vernest is tussen de termen van het product (het bevindt zich altijd tussen conjunctie en disjunctie van de termen).

Een divergentie-splitsing heeft dus twee vormen, h₁.h₂ en h₂.h₁. Beide vormen zijn evenwaardig om de metrische afstand tussen h₁ en h₂ te berekenen, afstand die altijd in twee dimensies kan uitgedrukt worden.