Een entiteit is gedefinieerd als datgene dat geteld kan worden. In de standaard taal zou het minder verwarrend zijn om altijd te spreken van een “entiteit-met-intensiteit” in plaats van een “entiteit”. Het begrip “entiteit” impliceert eigenlijk al een aantal, impliciet beschouwen we het als een soort, “iets” dat een aantal verschillende concrete verschijningen kan hebben, verschijningen die de soort, de “entiteit-met-intensiteit” niet karakteriseren. Alle “entiteiten-met-intensiteit” kunnen als welgevormde haakuitdrukking voorgesteld worden onder de voorwaarde dat de opspannende onderscheidingen dezelfde waarde hebben die verder niet gekend hoeft te zijn. Een entiteit wordt gemodelleerd door het patroon <x_i><<x>_i> dat inbedding symmetrisch is. Hier staat i voor het aantal onderscheidingen met dezelfde waarde <> of <<>>. Het getal i is een andere waarde dan de intensiteit van de entiteit. De intensiteit is het aantal verschillende verschijningen van de soort maar i is een aantal dat karakteristiek is voor de soort zelf, voor de entiteit, niet voor zijn intensiteit. Een individueel aspect x, noem dit x_K onderscheidt zich van een andere individuele x, noem deze x_L, behalve in de waarde die het aanneemt als het karakteristiek is voor de entiteit. Is i=1 dan is <x_i><<x>_i> de welgevormde haakuitdrukking <> en niet x, ook niet x↔<> (uitdrukking die niet anders is dan x), wel <>, een van de twee enige mogelijke waarden, of x↔x. Men zou dus kunnen stellen dat de welgevormde haakuitdrukking x als aspect van een entiteit niet telbaar is, geen entiteit kan zijn, om entiteit te zijn moeten er minimaal twee individuele welgevormde haakuitdrukkingen zijn en we moeten kunnen uitdrukken dat ze dezelfde waarde zouden kunnen hebben. Is i gelijk aan n dan is dit de welgevormde haakuitdrukking <x_n><<x>_n> die ervaringswaarde <> zou kunnen hebben, en indien dat het geval is wordt een entiteit ervaren. Een maximaal mogelijke entiteit in het hoogste onderscheidingen universum bevindt zich daarom altijd op atoombuur niveau (doordat het opgebouwd wordt door een complexe conjunctie of disjunctie van onderscheidingen met dezelfde waarde), maar aangezien onderscheidingen universa in elkaar vernest zijn zal een entiteit in een lager universum simultaan zijn met een entiteit in een hoger universum (inderdaad (met n en m natuurlijke getallen): als n onderscheidingen dezelfde waarde hebben, dan hebben ook n-m onderscheidingen dezelfde waarde). Simultane entiteiten kunnen ook deelentiteiten genoemd worden. Deelentiteiten worden door minder individuele onderscheidingen gekarakteriseerd dan de entiteiten waar ze deel van uitmaken. Door de ordening in de gehele getallen zijn dus ook deelentiteiten geordend en deze ordening is er een van aantallen individueel verschillende maar gelijkwaardige onderscheidingen die niet noodzakelijk een waarde toegekend kregen. Voorbeelden van deelentiteiten zijn te vinden in de voorbeelden van simultaneïteit.

Door het inbedding symmetrisch patroon kunnen entiteiten zich enkel op de even niveaus in een tralie bevinden. Dit onderbouwt ook dat één onderscheiding, bijvoorbeeld x, niet telbaar is. In het binair model is dit snel te zien omdat de veronderstelling impliceert dat de bits in een even aantal moeten voorkomen. Dit model maakt ook duidelijk dat elke welgevormde haakuitdrukking afgebeeld kan worden op een entiteit in een hoger universum door de volgende constructie: neem een willekeurige welgevormde haakuitdrukking met 2ⁿ bits. Construeer nu een welgevormde haakuitdrukking met 2ⁿ⁺¹ bits door de concatenatie van de 2ⁿ bits met 2ⁿ bits met een geïnverteerde volgorde. Deze welgevormde haakuitdrukking met 2ⁿ⁺¹ bits is de gezochte entiteit. Bijvoorbeeld 01100001 heeft een oneven verdeling van bits en kan dus geen entiteit zijn. De geïnverteerde bitstring is 10000110. Dus 01100001 kan afgebeeld worden op 01100001.10000110 in vier onderscheidingen met een even verdeling van bits en die dus een entiteit kan zijn, en inderdaad de volgorde van 01100001.10000110 inverteren verandert de welgevormde haakuitdrukking niet. Dit is een voorbeeld van <x_i><<x>_i> met i=2. In dat vier onderscheidingen universum is ook 01100001 te vinden als 01100001.01100001 en de geïnverteerde bitstring 10000110 als 10000110.10000110. Van dan af is het patroon 01100001.10000110 verder uit te breiden naar 01100001.10000110.01100001.10000110 in vijf onderscheidingen, dat is dan een voorbeeld van <x_i><<x>_i> met i=3 enz…. De ordening van entiteiten is een ordening van punten enkel op even niveaus en is dus onderscheiden van de ordening van simultaneïteit.

Het aantal entiteiten in een universum is dus het aantal welgevormde haakuitdrukkingen in een universum met één onderscheiding minder. Ook dit maakt duidelijk dat er een groot verschil is tussen de ordening van simultaneïteit (die ook mogelijk is tussen punten op aanliggende niveaus in een tralie, een ervan is even en de andere oneven) en de ordening van onderscheidingen universa (en dus verschillende tralies met meer of minder van deels dezelfde onderscheidingen). Het gevolg van dit alles is ook dat elkaar uitsluitende entiteiten enkel kunnen gemodelleerd worden vanuit elkaar uitsluitende toestanden in een universum met één onderscheiding minder. Voor elkaar uitsluitende entiteiten kunnen we de naam “object” gebruiken. Een object sluit een ander object uit omdat beide zich niet in dezelfde toestand kunnen bevinden, een van de onderscheidingen die nodig zijn om een object te beschrijven is bijvoorbeeld een ruimtelijke positie, en van ruimtelijke posities gaan we uit dat ze elkaar uitsluiten. In het hoogste universum bevindt een object zich in een bepaalde toestand en twee toestanden kunnen niet simultaan zijn. Maar dit geeft ook de mogelijkheid om toestanden en ook toestanden van een bepaalde soort te tellen. Dit is dan verder uit te breiden in de volgende zin: twee toestanden bepalen drie soorten, ze sluiten namelijk elkaar uit ten opzichte van een infimum en sluiten samen nog andere toestanden uit ten opzichte van andere infima en dat is niet de som van de toestanden die ze individueel uitsluiten. Maximale uitsluiting is elkaar twee-aan-twee uitsluiten. Dat doet zich enkel op atomair niveau voor. Dit legt eigenlijk het onderscheidingen universum vast. Dit is als volgt te zien met een voorbeeld: neem de vier AND-atomen in twee onderscheidingen in bitstring: 1110, 1101, 1011, 0111. Zij sluiten elkaar ook uit in drie onderscheidingen, want daar worden ze weergegeven als 11101110, 11011101, 10111011, 01110111 en daar bevinden ze zich niet meer op atomair niveau. Zij geven aanleiding tot vier elkaar uitsluitende entiteiten in het drie onderscheidingen universum die zich evenmin op atomair niveau bevinden: 11100111, 11011011, 10111101, 01111110. De soort “toestand” en “elkaar uitsluitende entiteit” op dat niveau sluiten elkaar niet uit.

Een soort kan gegeven worden door een welbepaald niveau in de tralie (we hebben immers toestanden geteld die zich op hetzelfde niveau bevinden en dus een bepaalde verhouding hoogbits versus laagbits gemeenschappelijk hebben en dus van een zelfde soort zijn). We hebben ook toestanden geteld zonder enige beperking van soort (dus zonder enige beperking van niveau in de tralie) door ons af te vragen hoeveel toestanden er zijn ten opzichte van één bepaalde keuze van toestand, zonder dat ze eenzelfde verhouding hoogbits versus laagbits vertonen. Tussen beide extremen moeten er dus ook verdelingen bestaan die we nog niet onderzocht hebben.

Toestanden kunnen dus ook van een bepaalde soort zijn en binnen een soort kunnen toestanden geteld worden aangezien ze elkaar uitsluiten. Dit geeft betekenis aan een begrip als “soorten som” of “soort eenheid die gesommeerd wordt”. Dit wordt concreter met een voorbeeld. Een som als soort kan bijvoorbeeld afgebeeld worden op een mogelijke partitie van een geheel getal en elk deel van de partitie kan dan als een soort beschouwd worden. Dit kan dan een dubbele interpretatie krijgen waartussen we een vrije keuze hebben. Bijvoorbeeld: het geheel getal 4 heeft 5 soorten partities want 4 kan opgesplitst worden in de volgende sommen waarbij de volgorde geen rol speelt (het is een soort partitie):

In de tabel wordt duidelijk dat de grootte van het deel van de partitie kan afgebeeld worden op een aantal entiteiten of op een niveau in de tralie. Voorbeeld van dit laatste: als we maar de tralie met 4 bits beschouwen dan beelden we de entiteit die door 4 toestanden gerealiseerd wordt af op een van de beide extremen, <> of <<>>, en de entiteit die door 3 atomaire toestanden gerealiseerd wordt beelden we af op een “tegenoverliggende” atomaire toestand van de entiteit die door 1 atomaire toestand gerealiseerd wordt. Andere voorbeelden van soorten zijn te vinden bij de voorbeelden van simultaneïteit die altijd gerelateerd zijn aan een niveauverschil in een tralie. De vrije keuze herkennen we ook met een voorbeeld: neem de partitie 2+1+1 (waarin we drie soorten eenheden herkenden), dan kunnen we toch zeggen dat 2 entiteiten zich in toestand A bevinden (een voorbeeld van interpretatie 1), een derde entiteit wordt door 1 toestand gerealiseerd (een voorbeeld van interpretatie 2) en een vierde entiteit wordt door 1 andere toestand gerealiseerd (eveneens een voorbeeld van interpretatie 2). We kennen dus een fundamentele beperking die we op twee gelijkwaardige manieren kunnen uitdrukken: een aantal entiteiten (en impliciet dus een aantal sporen of symbolen) of een aantal niveaus in de tralie (en impliciet dus een aantal onderscheidingen), en elke combinatie van die twee uitdrukkingen is gelijkwaardig.

Wanneer we de aantallen welgevormde haakuitdrukkingen per niveau berekenen dan wordt er nog een patroon duidelijk: voor een oneven niveau is het aantal gelijk aan een veelvoud van het aantal atomen, voor een even niveau is dit geen veelvoud, maar dit aantal is gelijk aan de som van het aantal entiteiten (en dus het aantal welgevormde haakuitdrukkingen op een bepaald niveau in een één lager universum) en een veelvoud van het aantal atomen. Dit wordt duidelijker met een voorbeeld, door de symmetrie in de tralie moet het voorbeeld maar voor de helft van het aantal niveaus gegeven worden.

In twee onderscheidingen met de entiteiten ontstaan uit één onderscheiding (die dus op het enige even niveau van het twee onderscheidingen universum terechtkomen):

In drie onderscheidingen met de entiteiten ontstaan uit twee onderscheidingen:

In vier onderscheidingen met de entiteiten ontstaan uit drie onderscheidingen:

In vijf onderscheidingen met de entiteiten ontstaan uit vier onderscheidingen:

We merken nu op dat de factoren van het aantal toestanden een zelfde fit geven met een Gauss curve als het aantal welgevormde haakuitdrukkingen (berekend als de minimalisering van de som van kwadratische verschillen). We berekenen de formule (laatste kolom) zoals bij de volledige tralie van vijf onderscheidingen (voorlaatste kolom):

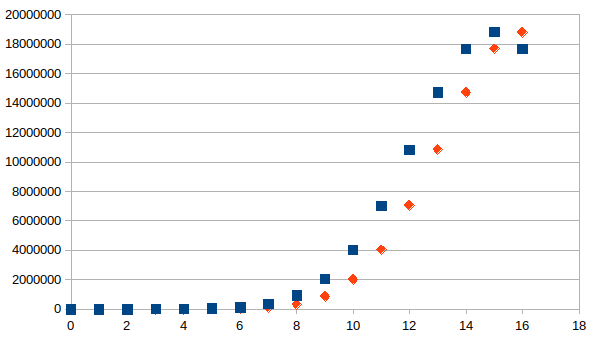
De grafiek voor de voorlaatste kolom hebben we elders al gegeven. Hieronder de grafiek voor de laatste kolom waarbij de berekende Gauss curve (vierkanten) gecentraliseerd is op x=15 en de verdeling van de aantallen in de tralie (ruiten) gecentraliseerd is op x=16 (om de passing te kunnen demonstreren).

Uiteraard kunnen we de sommen verder expanderen naar de verschillende “onderliggende” soorten, bijvoorbeeld met het laatste aantal: 601080390=12870+18783360*32=70+800*16+18783360*32==6+8*8+800*16+18783360*32=2+1*4+8*8+800*16+18783360*32=1*2¹+1*2²+8*2³+800*2⁴+18783360*2⁵. Zo kunnen we een nieuwe tabel samenstellen waarin de vernesting van onderliggende onderscheidingen universa (en dus soorten sommen) duidelijk te zien is:

Als we nu enkel de oneven niveaus weergeven dan komen de coëfficiënten van het hoogste universum duidelijk tot hun recht:

De coëfficiënten zijn gekend in de Online Encyclopedia of Integer Sequences (OEIS)als A281123. Er wordt daar aangetoond dat ze een “driehoek” T(n, k) vormen als volgt:

1

1

1, 1

1, 7, 7, 1

1, 35, 273, 715, 715, 273, 35, 1

1, 155, 6293, 105183, 876525, 4032015, 10855425, 17678835, 17678835, 10855425, 4032015, 876525, 105183, 6293, 155, 1

enz…

Ze worden gegenereerd als coëfficiënten van de volgende veeltermen:

q(0,x) = 1,

q(1,x) = x,

q(2,x) = x³ + x = x*(x² + 1),

q(3,x) = x⁷ + 7*x⁵ + 7*x³ + x = x*(x² + 1)*(x⁴ + 6*x² + 1),

q(4,x) = x¹⁵ + 35*x¹³ + 273*x¹¹ + 715*x⁹ + 715*x⁷ + 273*x⁵ + 35*x³ + x = x*(x² + 1)*(x⁴ + 6*x² + 1)*(x⁸ + 28*x⁶ + 70*x⁴ + 28*x² + 1),

enz...

We kunnen in vijf onderscheidingen ook expliciet enkel de rijen overhouden met simultane entiteiten zoals ze ontstaan uit toestanden ook in vier onderscheidingen, en dat zijn dan alle even niveaus:

We kunnen in vijf onderscheidingen expliciet enkel de rijen overhouden met simultane entiteiten zoals ze ontstaan uit toestanden ook in drie onderscheidingen en dat zijn dan alle niveaus die viervouden zijn:

We kunnen in vijf onderscheidingen expliciet enkel de rijen overhouden met simultane entiteiten zoals ze ontstaan uit toestanden ook in twee onderscheidingen en dat zijn dan de niveaus die achtvouden zijn:

En uiteraard geeft niveau 16 ook de simultane entiteiten zoals ze ontstaan uit toestanden ook in één onderscheiding.

Besluit

Entiteiten kunnen zich niet op oneven niveaus bevinden. De punten op de oneven niveaus kunnen niet op een lager onderscheidingen universum afgebeeld worden. Dit is altijd zo voor het grootste universum. Het atomair niveau is oneven en hier bevinden zich dus geen entiteiten, enkel toestanden. Er is dus minstens één onderscheiding van het hoogste universum die entiteiten niet karakteriseert en enkel een individuele toestand karakteriseert (aangezien alle toestanden elkaar wederzijds uitsluiten).

Aangezien alle getallen als (relaties tussen) binomiaal coëfficiënten ontstaan kunnen veel relaties ontdekt worden die al bekend zijn bij het onderzoek naar de vermenigvuldiging van veeltermen, maar die nog niet geïnterpreteerd werden in de context van ervaarbare aspecten.

Het niveau waarop de waarschijnlijkheid dat er zich een entiteit bevindt het kleinst is, is het atoombuur niveau (de waarschijnlijkheid is nul op het atomair niveau). In 5 onderscheidingen en dus met 2³²=4294967296 mogelijkheden (welgevormde haakuitdrukkingen), is die waarschijnlijkheid 2⁴/2³²=16/4294967296=3,72529029846.10^-9. Het niveau waarop de waarschijnlijkheid dat er zich een entiteit bevindt het grootst is, is het centraal niveau. Het centraal niveau is altijd even, behalve voor één onderscheiding. Dit aantal is een som van aantallen die ook in minder onderscheidingen kunnen uitgedrukt worden (en die dus deelentiteiten zijn). In 5 onderscheidingen kunnen zich 12870 entiteiten bevinden op het meest waarschijnlijke niveau, dat is dus de fractie 12870/601080390=2,14114454807.10^-5. De waarschijnlijkheid dat een mogelijkheid (een mogelijke welgevormde haakuitdrukking) zich op dat meest waarschijnlijke niveau bevindt is 601080390/4294967296=0,139949934091, maar de waarschijnlijkheid dat dit een entiteit is, is dus 12870/4294967296=2,99653038383.10^-6. Dit niveau is het centraal niveau in vijf onderscheidingen en is dus ook het niveau met de meeste simultane entiteiten, entiteiten van een verschillende soort (en in dit geval dus 1 in 1 onderscheiding, 1 in 2 onderscheidingen, 8 in 3 onderscheidingen, 800 in 4 onderscheidingen want 1*2¹+1*2²+8*2³+800*2⁴=12870).