en
Door één keuze te maken is een willekeurige haakvector H voor te stellen als een koppel (h1, h2) waarbij h1 staat voor de haakvector overeenkomend met de ene kant in de splitsing en h2 staat voor de haakvector overeenkomend met de andere kant in de splitsing. Zo een koppel hebben we al onderzocht bij de afstanden die kunnen onderscheiden worden in het binair model.
Het koppel (h1, h2) noemen we een 1-splitsing.
Een koppel (h1, h2) heeft een ordening, en inderdaad kunnen we zowel in de bitstring als in de welgevormde haakuitdrukking vaststellen dat commuteren gewoonlijk leidt tot een ander resultaat. Dit hebben we ook vastgesteld bij het creatief product: <x<h1>><<x><h2>> en <x<h2>><<x><h1>> zijn in het algemeen verschillend. En ook: twee delen van een bitstring wisselen geeft over het algemeen een ander resultaat.
Een 1-splitsing is dus een geordende lijst van haakvectoren.
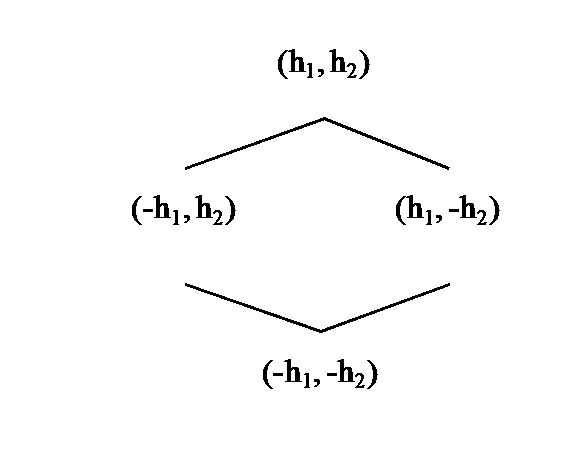
Met een koppel kunnen we dan nieuwe koppels genereren waarmee twee tralies te construeren zijn die volledig isomorf zijn met deze van het één-onderscheiding universum:

en

Het
koppel (h1, h2) genereert dan twee 1-splitsing
universa die gekarakteriseerd worden doordat de twee zijden van de
splitsing onderling verwisseld worden.
De koppels maken het nu mogelijk om een operator model te construeren voor het haakformalisme. Dat zullen we op twee manieren doen:
Deze operaties kunnen we een naam geven, bijvoorbeeld 1(h1, h2) als de identiteitsoperator die (h1, h2) omzet in (h1, h2). Dan kunnen we -1(h1, h2) als de inbeddingsoperator zien die (h1, h2) omzet in (-h1, -h2). Noem nu e(h1, h2) de operator die (h1, h2) omzet in (-h2, h1) zoals in de laatste tralie. We merken nu op dat, als we nog eens deze operator uitvoeren op het resultaat, we (-h1, -h2) genereren. Anders uitgedrukt: e(e(h1, h2)) resulteert in -1(h1, h2). Hiermee hebben we een operator waarvan het kwadraat resulteert in de inbedding van de identiteitsoperator.
We kunnen de operaties voorstellen als matrices als operatoren en we zullen ze afbeelden op 2x2 matrices die dan kunnen ageren op 1-splitsingen die voorgesteld worden als een geordende lijst van twee haakvectoren.
We benadrukken expliciet dat het 1-splitsing universum gedefinieerd is onafhankelijk van de universa waarin h1 en h2 uitgedrukt zouden zijn. Daarenboven moeten we niet veronderstellen dat h1 en h2 in hetzelfde universum moeten uitgedrukt worden want het overkoepelend universum dat toelaat de relaties tussen h1 en h2 uit te drukken wordt in de operator gecodeerd. Veronderstellen we nu wel dat h1 en h2 in hetzelfde universum uitgedrukt worden dan kunnen we het speciaal geval van de orthogonale involutie onderzoeken.
Dit model moet niet verward worden met het model voor divergentie en convergentie van universa, hoewel natuurlijk beide onder voorwaarden met elkaar gerelateerd zijn. De voorwaarde is de volgende: in het 1-splitsing model gebruiken we het gegeven dat <> fijner is dan <<>>, en we zouden zowel h1 als h2 kunnen beschouwen als coëfficiënten van <<>>. In het model voor divergentie gebruiken we het gegeven dat h2 fijner is dan h1 en, indien we dat zouden willen, zou elk van deze welgevormde haakuitdrukkingen een coëfficiënt kunnen krijgen.