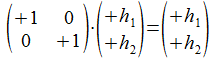
We onderzoeken nu de meest primitieve operaties die in staat zijn te opereren op een 1-splitsing. De haakvector h zullen we daarbij voorstellen als het koppel (h1, h2) waarbij h1 staat voor de string overeenkomend met de eerste term in de 1-splitsing en h2 staat voor de string overeenkomend met de tweede term in de 1-splitsing. We veronderstellen hierbij niets over de welgevormdheid van de haakuitdrukkingen.
De identiteit stellen we voor als de operatie ε dus ε(h1, h2) is niet te onderscheiden van (h1, h2) en -ε(h1, h2) is niet te onderscheiden van (-h1, -h2).
In matrix formaat:
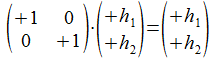
Wat ook de componenten van h zijn, deze matrix is de identiteitsmatrix.
Kwadrateren van deze operatie levert terug de identiteitsmatrix.
Voor de tegengestelde signatuur vinden we:
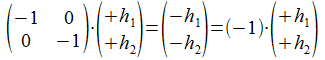
Wat ook de componenten van h zijn, deze matrix genereert de uitwendige involutie van h.
Kwadrateren van deze operatie levert terug de identiteitsmatrix.
De operatie υ, dus υ(h1, h2) is niet te onderscheiden van (h2, h1) en -υ(h1, h2) is niet te onderscheiden van (-h2, -h1).
In matrix formaat:
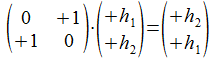
Kwadrateren van deze operatie levert hetzelfde terug de identiteitsmatrix ε op, ook kwadrateren van de uitwendige involutie levert terug de identiteitsmatrix ε op.
De operatie ν, dus ν(h1, h2) is niet te onderscheiden van (h1, -h2) en -ν(h1, h2) is niet te onderscheiden van (-h1, h2).
In matrix formaat:
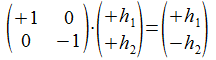
Kwadrateren van deze operatie levert terug de identiteitsmatrix ε, ook voor de uitwendige involutie.
De operatie νυ, dus νυ(h1, h2) is niet te onderscheiden van (h2, -h1) en -νυ(h1, h2) is niet te onderscheiden van (-h2, h1). Hierin is de operatie de matrix vermenigvuldiging. Als we nog eens de operatie -νυ uitvoeren is het resultaat het koppel (-h1 , -h2). We beschikken dus nu over een operatie op koppels waarvan het kwadraat overeenkomt met een vermenigvuldiging met -1, anders gezegd komt de operatie overeen met de wortel nemen uit -1.
In matrix formaat:
![]()
Het is duidelijk wat de inbedding van beide leden van de vergelijking oplevert.
Kwadrateren van deze operatie levert -ε op, en hiermee is de operator νυ de enige van de primitieve operaties met deze eigenschap.
νυ ontstaat als matrix vermenigvuldiging van ν met υ
![]()
-νυ ontstaat als matrix vermenigvuldiging van υ met ν en is dus niet verschillend van υν
![]()
De introductie van de techniek van matrices, en in het bijzonder de matrix vermenigvuldiging introduceert een niet-commutativiteit. Dit komt niet overeen met de eigenschappen van de vectorvermenigvuldiging (transformatie) in het haakformalisme (zie het verschil tussen νυ en υν). De enige niet-commutatieve operatie in het haakformalisme is het creatief product. De introductie van matrices veronderstelt dus dat een creatief product als enige operatie gebruikt wordt. Door matrices te gebruiken voert men dus minstens één extra onderscheiding toe, en inderdaad is dit de interpretatie van de 1 splitsing die één extern standpunt introduceert. We zullen moeten construeren hoe dat dan wel gebeurt en zo zullen we de vooronderstellingen van matrix techniek kunnen blootleggen. Aangezien elke welgevormde haakuitdrukking als een creatief product kan uitgedrukt worden kan een gedetailleerde uitwerking van een vertaling van het haakformalisme in matrix formaat tot bijkomende inzichten leiden in het repertorium van matrices.
Het 1-splitsing universum genereert dus de matrix vermenigvuldiging die dan ook een nieuwe operatie is die een geordende combinatie is van som en vectorvermenigvuldiging (transformatie). Die ordening wordt gekarakteriseerd doordat ze de gekozen splitsing (in dit geval een 1-splitsing) in alle operaties respecteert.