We hebben al een
proces met een constante eigenwaarde onderzocht. Binnen één
overkoepelend systeem zullen we nu simuleren dat meerdere processen
(met eventueel verschillende eigenwaarden resulterend in zowel
positieve als negatieve feedback) de intensiteit veranderen en dat
dit resulteert in een (simulatie van) gedrag dat waarneembaar is in
het overkoepelend systeem.
Door de studie van één proces blijkt dat de intensiteit van een
entiteit bij elke processtap (bijvoorbeeld in de tijd) exponentieel
verandert. De berekende intensiteit (1±k)n is niet anders
is dan een product van n dezelfde termen, dus Πn(1±k).
We willen daarom eerst het model van het getalproduct zelf beter
begrijpen.
Betekenis van het product model
We starten de analyse door te veronderstellen dat na het bereiken
van stap 2 de factor k gewijzigd wordt naar k' en dan stabiel blijft
tot n. We bouwen terug de
tabel op voor de positieve feedback.
Tijdstap
|
Positieve feedback
|
0
|
(x-x0)
|
1
|
(x-x0)+k(x-x0)=(x-x0)(1+k)
|
2
|
(x-x0)+k(x-x0)+k{(x-x0)+k(x-x0)}=(x-x0)(1+2k+k2)
|
3
|
(x-x0)+k(x-x0)+k{(x-x0)+k(x-x0)}+k'{(x-x0)+k(x-x0)+k{(x-x0)+k(x-x0)}}=(x-x0){(1+2k+k2)+k'(1+2k+k2)}=(x-x0)(1+2k+k2)(1+k')
|
...
|
...
|
n
|
(x-x0)(1+k)2(1+k')n-2
|
Hieruit volgt dat (1+k)m zich zal gedragen als een
constante voor alle stappen groter dan m tot de stap n. In het
voorbeeld is m=2. We merken ook op dat dit compatibel is met (1+k)m
∝(1-k)-m.
In deze redenering hebben we niets verondersteld over k', dus deze
kan evenzeer kleiner zijn dan nul, waarmee dan negatieve feedback
gemodelleerd wordt. In de limiet kan men dan ook voor elke stap een
andere k veronderstellen en op stap n wordt dan (x-x0)Πn(1+km)m’
bereikt waarbij km zowel positief als negatief kan zijn.
Het product is dus een product van n termen en m’ is kleiner dan of
gelijk aan n, en de som van verschillende m is gelijk aan n. We
merken dus op dat (x-x0)(1+k)n voor een
bepaalde k en n ook kan geïnterpreteerd worden als de evaluatie van
de relatie (x-x0)Πν(1+κ) op het punt n en k,
waarbij zowel ν als κ variabelen zijn en -1<κ<+1. Dit toont
dus het meest algemene product model.
Dit is een opmerkelijk resultaat voor een interpretatie van de
processtappen n als “stappen in de tijd”. Het geeft aan dat “de
chronologie” van het proces in dit model geen rol hoeft te spelen,
enkel het aantal stappen (de intensiteit van de eenheid “stap”)
en de betrokken eigenwaarden. Dit wordt duidelijk met een voorbeeld:
veronderstel 8 stappen en drie eigenwaarden k, k’ en k’’.
Veronderstel dat er bij stap 8 de volgende relatie geldt:
(x-x0)(1+k)2(1+k’)(1+k'’)8-3. We
kunnen ons nu voorstellen dat deze relatie op verschillende manieren
chronologisch ontstaan kan zijn. Laten we de veronderstelde
chronologie als de nevenschikking van de termen na (x-x0)
weergeven, met een uitbreiding van de nevenschikking geïnterpreteerd
als een volgende stap in de tijd. Bijvoorbeeld: de chronologie
(x-x0)(1+k)(1+k’)(1+k'’)5(1+k) is
gelijkwaardig met de chronologie
(x-x0)(1+k'’)3(1+k’)(1+k)(1+k'’)2(1+k)
enz.… Dit impliceert ook dat er geen andere stap is dan de stap van
het proces, dus bij één stap kan er simultaan een (1±k), een
(1±k’), een (1±k'’)2, …, een (1±km’)n
een invloed uitoefenen. Inderdaad: simultaneïteit in een tralie die
gebouwd wordt in het getallendomein hebben we kunnen modelleren als
het getalproduct dat een eenheid vormt op een dieper niveau dan
het atoom niveau.
Hieruit volgt dus ook dat (x-x0)(1±k)n voor
een bepaalde k en n ook kan geïnterpreteerd worden als de simultane
invloed van n aspecten (1±k) en dat is uiteraard compatibel met de
simultaneïteit van (x-x0)(1±k)n-m met
(x-x0)(1±k)n voor m<n.
Met een product zullen we dus simultane interacties van
eigenwaarden modelleren, in tegenstelling met een som (die enkel zin
heeft als de elementen van de som elkaar uitsluiten). Zoals we
aantoonden ligt simultaneïteit aan
de basis van causaliteit. Dit toont aan wat de relatie van “de
klassieke tijd” is met het aantal stappen n.
Beschrijving en interpretatie met één
eigenwaarde
Het onderzoek naar de interpretatie van simultane interacties
beginnen we met de relaties van de intensiteit van het verschil dat
een verschil maakt (getal) met de stappen grafisch voor te stellen.
Dit doen we voor de vier mogelijke feedback processen. Hierbij kunnen
we al onmiddellijk een eerste gevolg afleiden: zowel k speelt een
rol, maar daarenboven speelt evenzeer een constante factor een rol
(waarvoor we hieronder het getal 0 kiezen). Bij de negatieve feedback
speelt de constante een rol als doel dat nooit bereikt wordt maar dat
geanticipeerd kan worden, bij de positieve feedback speelt de
constante de rol van startpunt waarvan nooit vertrokken wordt maar
dat achteraf gereconstrueerd kan worden.
In de voorbeelden in de onderstaande tabel is k=0,2 en zijn 30
stappen weergegeven, we kunnen de stappen interpreteren als tijd of
niet, essentieel is dat de stappen elkaar uitsluiten:
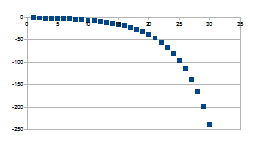
0-(1+k)n
|
Wordt kleiner vanaf -1-k naar verdere -
|
Positieve feedback in de negatieve zin
|
|
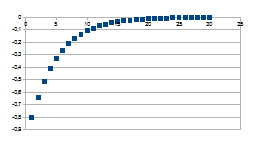
0-(1-k)n
|
Wordt groter vanaf -1+k dichter naar 0
|
Negatieve feedback in de positieve zin
|
|
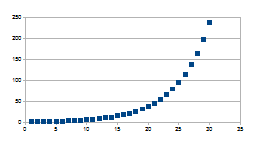
0+(1+k)n
|
Wordt groter vanaf 1+k naar verdere +
|
Positieve feedback in de positieve zin
|
|
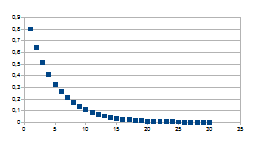
0+(1-k)n
|
Wordt kleiner vanaf 1-k dichter naar 0
|
Negatieve feedback in de negatieve zin
|
|
Wat vanuit de grafische voorstelling onmiddellijk opvalt is dat de
positieve feedback steeds verder divergeert naar verschilwaarden die
verder toenemen (het verschil van de intensiteiten op stap n en stap
n+1 wordt steeds groter) en dat de negatieve feedback steeds verder
convergeert naar verschilwaarden die verder afnemen (het verschil van
de intensiteiten op stap n en stap n+1 wordt steeds kleiner).
Dit heeft grote praktische gevolgen voor elke waarnemend agens.
Deze is immers beperkt in waarnemingsresolutie, wat we kunnen
modelleren als het “venster”, het interval dat op de as van de
intensiteiten overeenkomt met een interval op de as van de stappen.
Aan dit venster kunnen we twee karakteristieken toekennen: het
interval is een verschil (eerste karakteristiek) op een bepaald
verschil van een nulpunt (tweede karakteristiek). Bijvoorbeeld: er
kan maar een intensiteitsverschil waargenomen worden van een minimale
grootte van 100 en maximale grootte van 105
(bijvoorbeeld tussen 102 en 107) vanaf een
intensiteit van minimaal 10-3 tot maximaal 1010.
Bijvoorbeeld: ziende agentia stellen hun sensor in op een gemiddelde
lichtintensiteit en kunnen dan slechts een beperkt aantal
intensiteitsverschillen waarnemen. Wat buiten die grenzen valt is
geen verschil meer dat een verschil maakt.
Voor de positieve feedback is er een stap waarbij er niets meer
waarneembaar is omdat de maximaal (minimaal) waarneembare intensiteit
overschreden wordt of het verschil tussen de stappen het maximaal
verschil overstijgt. Als we de stappen als tijd interpreteren komt
dit overeen met een moment in de toekomst, interpreteren we de
stappen niet als tijd dan komt dit overeen met een grotere schaal.
Een positieve feedback proces explodeert of dooft uit en daarna “is
er geen proces meer” omdat er geen output meer waarneembaar is. Een
positieve feedback proces “begint nooit” (is met grote
onzekerheid te reconstrueren) en eindigt in een big bang of big
crunch. Wat ook de toestand op stap n was, voor de positieve feedback
is het resultaat altijd verschillend van nul (wat we kunnen
interpreteren als "ooit waarneembaar") omdat gelijk welk,
eventueel onwaarneembaar of niet relevant geacht, verschil (in het
verleden bijvoorbeeld, of op een bepaalde schaal) in de loop van het
proces uitvergroot wordt (en dan waarneembaar en relevant kan
worden).
Voor de negatieve feedback is er een stap (bijvoorbeeld een moment
in het verleden, of een kleinere schaal) waarbij er niets
waarneembaar is, een proces wordt plots waargenomen met een bepaalde
intensiteit van output en blijft output genereren, hoe ver men ook in
de toekomst of in de ruimte gaat: de output bereikt een attractor
gebied waarbij de attractor evenwel nooit bereikt wordt. Een
negatieve feedback proces begint in een big bang of big crunch
(bijvoorbeeld een plots inzicht) en eindigt nooit hoewel de
waarneming ervan onder de waarnemingsresolutie kan zakken. Voor de
negatieve feedback geldt dat wanneer de toestand op stap n niet
verschillend waargenomen wordt van de huidige toestand die het
referentiepunt is, het resultaat nul is (wat we kunnen interpreteren
als "niet waarneembaar") en nul blijft. Het is duidelijk
dat een verschil dat geen verschil maakt niet anders is dan de
waarnemingsresolutie van het agens. Een verschil dat geen verschil
maakt geeft ook de
logische onderbouwing die de nul genereert en die dus de volle
wiskundige modellering zinvol maakt. De kwantitatieve meting van
relevante verschillen is dus gemakkelijk te simuleren (te
anticiperen) door een hedendaags computer proces te gebruiken, maar
geeft tezelfdertijd de grens aan van elke simulatie: de huidige
toestand bevat alle informatie om de volgende toestand grotendeels
te anticiperen (hoewel in werkelijkheid ook een niet te
anticiperen gebeurtenis zal optreden). Een simulatie is in een
beperkte mate relevant voor het werkelijk optredend proces maar is
bijvoorbeeld zeer waardevol om aan te geven hoe lang het agens wil en
kan wachten om een volgende actie uit te voeren.
Laten we het inzicht iets specifieker met processen in de tijd
illustreren. De constructie van zowel positieve als negatieve
feedback (re)construeert
het verleden: bij positieve feedback hoeft er in het verleden
geen doel gekozen te zijn, er kan gebeuren wat er gebeurt en er is
steeds meer dat er kan gebeuren, in die zin is sturen op positieve
feedback geen doelgerichte sturing maar vergroot een initieel
eventuele kleine afwijking (een eventueel klein verschil dat "nog"
geen verschil maakt). Het proces verwijdert zich meer en meer van een
startpunt dat nooit “aanwezig was” maar als anti-doel kan
beschouwd worden. Positieve feedback is dus het mechanisme waarmee
het mogelijk wordt “iets anders” te bereiken of iets
(bijvoorbeeld een ongewenste entiteit) volledig te vernietigen of
onwaarneembaar te maken. Daarentegen moet bij negatieve feedback een
doel niet alleen in het verleden maar ook in de toekomst
beschikbaar zijn: iets moet waarneembaar zijn maar ook blijvend
waarneembaar zijn in het proces hoewel het pas op één bepaald
moment “uit het niets opduikt” en hoewel het na verloop van tijd
buiten de waarnemingsresolutie zal vallen en dus niet meer
waargenomen zal worden. Als negatieve feedback gebruikt wordt om te
sturen dan is dit "bewust gewilde" doel een attractor van
het gestuurde proces. Het mechanisme van de negatieve feedback is de
anticipatie hoe een intensiteit naar een bepaalde waarde kan gestuurd
worden, dus hoe het verschil ten opzichte van die waarde gereduceerd
kan worden zonder dat het volledig verdwijnt hoewel het
onwaarneembaar kan worden. Indien er enkel het mechanisme van de
negatieve feedback beschikbaar zou zijn, dan zou er nooit iets kunnen
veranderen. Ondanks het feit dat de getalmatige formulering in
dezelfde vorm kan uitgedrukt worden, toch is er een zeer groot
verschil voor operationeel verifieerbare uitspraken. Positieve en
negatieve feedback zullen altijd samen voorkomen, al was het maar
omdat ze in elkaar uit te drukken zijn ((1+k)n ∝(1-k)-n).
Positieve feedback kan zorgen voor een niet te voorspellen
verrassing eens het proces van de exponentiële groei een
waarneembare toestand bereikt (in positieve zin) of volledig
verdwijnt (in negatieve zin) en nog niet het waarneembare interval
overschrijdt. Positieve feedback is bijvoorbeeld te zien bij de groei
van cellen of bacteriën: hun aantal zal blijven groeien zolang
materiaal en energie beschikbaar is (aangevoerd kan worden), tot een
bepaalde grens bereikt is waarbij niet genoeg materiaal en energie op
de plaats van de transformatie meer beschikbaar is en verdere groei
onmogelijk wordt. Positieve feedback kan zowel gewenst zijn
(verandering is nodig) als gevaarlijk zijn (verandering moet vermeden
worden) en met de aanvoer van materiaal en energie kan dat gestuurd
worden (dit is dan de negatieve feedback). Dit moet blijken in
werkelijkheid, enkel het explosief karakter is voorspelbaar, wat in
werkelijkheid zal bereikt worden is niet te anticiperen, hangt
onvermijdelijk samen met negatieve feedback, is een dynamisch
gegeven, en eens een evenwicht bereikt is zal elke "afwijking
van het evenwicht" dan onmogelijk worden door het bestaan van de
negatieve feedback.
Het relatief verschil tussen twee eigenwaarden
We kunnen nu k variëren en op die manier gedragseigenschappen van
deelprocessen in een groter geheel met zelfde tijdstap ten opzichte
van elkaar onderscheiden. In de voorbeelden in de onderstaande tabel
is k=0,8 en zijn 30 stappen in de tijd weergegeven en houden we de
constante factor nog steeds op 0:
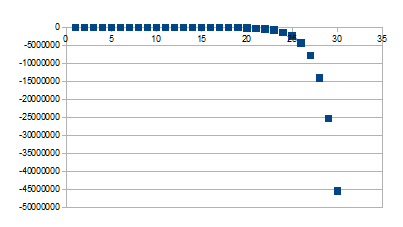
0-(1+k)n
|
Wordt kleiner vanaf -1-k naar verdere -
|
Positieve feedback in de negatieve zin
|
|
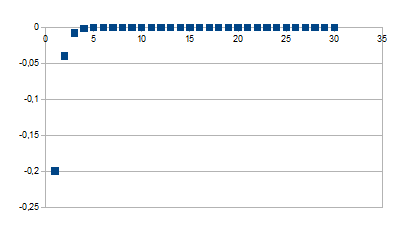
0-(1-k)n
|
Wordt groter vanaf -1+k dichter naar 0
|
Negatieve feedback in de positieve zin
|
|
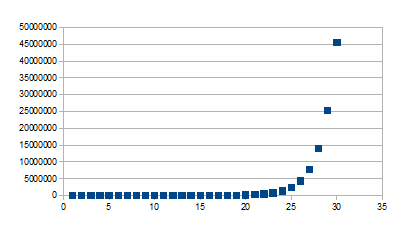
0+(1+k)n
|
Wordt groter vanaf 1+k naar verdere +
|
Positieve feedback in de positieve zin
|
|
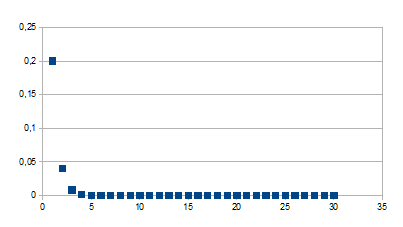
0+(1-k)n
|
Wordt kleiner vanaf 1-k dichter naar 0
|
Negatieve feedback in de negatieve zin
|
|
We kunnen nu de volgende kwalitatieve uitspraak doen: hoe groter k
(hoe kleiner de verdubbelingstijd/halveringstijd) hoe langer de
intensiteit zich in een heel klein gebied bevindt ten opzichte van
het hele intensiteitsbereik, zodanig dat de intensiteitsverschillen
bij de verschillende stappen in dat gebied misschien niet meer groter
zijn dan de waarnemingsresolutie van het "agens met een grotere
k". Dan kan het agens de verschillende tijdstappen niet meer
onderscheiden omdat het gerelateerde intensiteitsverschil buiten zijn
waarnemingsgevoeligheid ligt. Het doel dat nooit bereikt kan worden
maar dat geanticipeerd kan worden, wordt dus door het "agens met
een grotere k" beschouwd als "bereikt" (negatieve
feedback) omdat het geen verschil meer waarneemt. Het startpunt
(positieve feedback) waarvan nooit vertrokken wordt maar dat
gereconstrueerd kan worden wordt door het "agens met een grotere
k" met een veel grotere onnauwkeurigheid achteraf
ge(re)construeerd: het kan in een heel gebied van mogelijke stappen
liggen. Hierbij moeten we goed beseffen dat dit een kwalitatieve
uitspraak is ten opzichte van een intensiteitsbereik van deze
specifieke "agens met een grotere k". Om dit te illustreren
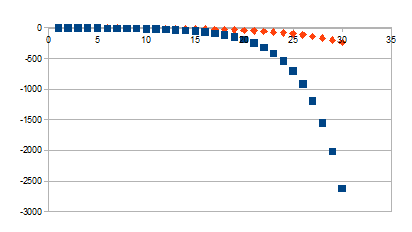
tonen we in de onderstaande tabel een vergelijking tussen een curve
voor k=0,3 en voor k=0,2 (we kiezen een relatief klein verschil om
het effect waarneembaar te maken (!) op de resolutie van de grafiek).
De waarden voor k=0,3 zijn met een vierkant symbool aangegeven, de
waarden voor k=0,2 zijn met een ruitsymbool aangegeven.
0-(1+k)n
|
Wordt kleiner vanaf -1-k naar verdere -
|
Positieve feedback in de negatieve zin
|
|
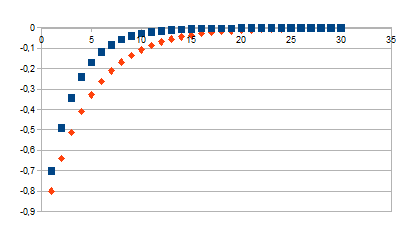
0-(1-k)n
|
Wordt groter vanaf -1+k dichter naar 0
|
Negatieve feedback in de positieve zin
|
|
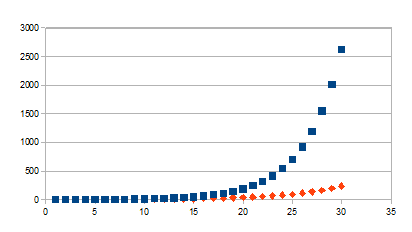
0+(1+k)n
|
Wordt groter vanaf 1+k naar verdere +
|
Positieve feedback in de positieve zin
|
|
0+(1-k)n
|
Wordt kleiner vanaf 1-k dichter naar 0
|
Negatieve feedback in de negatieve zin
|

|
Dit maakt duidelijk dat ten opzichte van elkaar het "agens
met een grotere k" sneller het geanticipeerde gedrag realiseert,
of het nu positieve of negatieve feedback is. Toch zien we een
duidelijk verschil tussen positieve en negatieve feedback als we de
waarden in ordinaat bekijken. De intensiteit is bij negatieve
feedback per definitie begrensd in absolute waarden tussen 0 en 1,
bij positieve feedback is de intensiteit in dit voorbeeld begrensd in
absolute waarden tussen 0 en 3000, maar die afstand is natuurlijk
willekeurig groot te maken. Beide effecten samen kunnen we als volgt
verwoorden: hoewel het "agens met een grotere k" sneller
het geanticipeerde gedrag realiseert is dit misschien voor zichzelf
niet waarneembaar voor de positieve feedback als zijn
waarnemingsresolutie beperkt wordt door het veel grotere bereik dat
moet gerealiseerd worden om waarneembaar te zijn (een verschil te
maken dat een verschil maakt). Deze agens moet immers toestanden
onderscheiden die elkaar uitsluiten om enige zin te kunnen geven aan
het begrip “stap”. Aangezien we nu veronderstellen dat beide
agentia deelprocessen vertegenwoordigen van een globaal proces
(waaraan ze dus beide onderhevig aan zijn, een proces met k=1) dan
kunnen we dit interpreteren dat het "agens met een kleinere k"
veel gevoeliger kan zijn voor verandering bij opeenvolgende
tijdstappen, verandering die voor deze agens als elkaar uitsluitend
kunnen gewaardeerd worden terwijl ze voor het "agens met een
grotere k" nog niet binnen zijn resolutiebereik ligt (het
verschil dat moet waargenomen kunnen worden). We
tonen aan dat de grootte van de k gerelateerd is met de
waarschijnlijkheid dat het agens actie zou ondernemen, een
grotere k en dus een kleinere verdubbelingstijd of halveringstijd,
zou dan een agens meer tot actie bewegen. Dit is dan een eerste
indicatie voor het belang van de verscheidenheid binnen een systeem
van waarnemende deelsystemen omdat verscheidenheid hoe dan ook
gerelateerd is met “een verschil dat een verschil maakt”. Elk
waarnemend deelsysteem dat zich van een ander deelsysteem
onderscheidt, zal onvermijdelijk in een ander gebied gevoelig zijn en
vroeger of later uitgedaagd of aangespoord worden tot het nemen van
actie. En het meest opmerkelijke is dat dit geldt voor de positieve
feedback en op een “genormaliseerde” manier (“tussen 0 en 1”)
geldt voor de negatieve feedback! Negatieve feedback (of
doelgerichtheid naar een te anticiperen attractor die
nooit bereikt wordt) heeft voldoende aan eenzelfde soort
waarnemingsgevoeligheid voor alle deelsystemen en het deelsysteem met
kleinere k (en dan een grotere halveringstijd realiseert en dus
trager naar het doel evolueert) zal langer een onzekerheid verdragen
dan een deelsysteem met grotere k. Deze laatste zal sneller actie
ondernemen bij een afwijking van de geanticipeerde attractor.
We kunnen nog een andere belangrijk verschil beklemtonen dat het
duidelijkst is bij de positieve feedback in positieve zin en de
negatieve feedback in negatieve zin. Bij de positieve feedback (in
absolute waarde) impliceert de intensiteit van de grotere k deze van
de kleinere k, maar bij de negatieve feedback (in absolute waarde)
impliceert de intensiteit van de kleinere k deze van de grotere k.
Implicatie is hier gebruikt als de interpretatie
van simultaneïteit: de grotere intensiteit van een eenheid
impliceert een kleinere intensiteit van dezelfde eenheid. Met een
voorbeeld: als er vier koeien in de weide staan impliceert dat dat er
ook drie staan, en als een koe 600kg weegt dan impliceert dat dat ze
ook 200kg vlees kan opleveren.
Eenzijdige begrenzing en som
De som ±C±(1±k)n is eenzijdig begrensd door de keuze
van k. De eigenwaarde hebben we moeten kiezen tussen 0 en 1. Bij de
keuze k=0 is er geen feedback, bij de keuze k=1 is er enkel positieve
feedback en geen negatieve feedback. We kiezen nu een ±k als start
punt.
+k-(1+k)n
|
Wordt kleiner vanaf -1 naar verdere -
|
Positieve feedback in de negatieve zin
|
-k-(1-k)n
|
Wordt groter vanaf -1 dichter naar 0
|
Negatieve feedback in de positieve zin
|
-k+(1+k)n
|
Wordt groter vanaf +1 naar verdere +
|
Positieve feedback in de positieve zin
|
+k+(1-k)n
|
Wordt kleiner vanaf +1 dichter naar 0
|
Negatieve feedback in de negatieve zin
|
We veronderstellen nu een coëfficiënt voor (1±k)n.
Dit modelleert een som van een aantal (namelijk c) van dezelfde
(1±k)n die de dynamiek genereert. Aangezien ±c(1±k)n
voor een bepaalde n niet meer kan onderscheiden worden van de
intensiteit (1±k)m zal de keuze voor een intensiteit c
(die we dan kunnen schrijven als (1±k)m-n) niets
veranderen aan het patroon. We kunnen dus ook schrijven:
+ck-c(1+k)n
|
Wordt kleiner vanaf -c naar verdere -
|
Positieve feedback in de negatieve zin
|
-ck-c(1-k)n
|
Wordt groter vanaf -c dichter naar 0
|
Negatieve feedback in de positieve zin
|
-ck+c(1+k)n
|
Wordt groter vanaf +c naar verdere +
|
Positieve feedback in de positieve zin
|
+ck+c(1-k)n
|
Wordt kleiner vanaf +c dichter naar 0
|
Negatieve feedback in de negatieve zin
|
Er is dus een samenspel te modelleren van de constante term c (het
doel of anti-doel) en de variabele term (1±k) in de som ±ck±c(1±k)m.
Het ligt nu voor de hand om de constante term ook door een variabele
term te vervangen zodanig dat ook positieve feedback en negatieve
feedback met elkaar gesommeerd kunnen worden binnen één systeem
(met dezelfde eenheid).
De interpretatie hiervan is de volgende: een som van twee
variabele termen (die de intensiteit geven van een eenheid in een
proces) is slechts gedefinieerd als beide processen onafhankelijk
zijn. Ze zullen dan voor elkaar als een referentiepunt functioneren.
Een som van (1+k) en (1-k), dus met zelfde k zal geen evenwicht
bereiken, beide processen evolueren in dezelfde zin, een verschil van
(1+k) en (1-k) (dus met zelfde k) bereikt evenmin een evenwicht, maar
een intensiteit die evenredig is met de eigenwaarde.
Een klassiek voorbeeld hiervan is een badkuip met een kraan om
water toe te voeren en een kraan om water af te voeren, waarbij het
debiet van beide kranen “op dezelfde manier” (met zelfde
eigenwaarde k) afhankelijk is van de hoeveelheid water in de badkuip
maar waarbij beide kranen onafhankelijk van elkaar bediend worden. De
bediening is het proces en dat kan een positief feedback proces zijn
of een negatief feedback proces. De praktische toepassing voor het
beheerst vullen van de badkuip is dat de toevoer een negatief
feedback proces is: hoe meer water in het bad, hoe minder water
toegevoegd wordt. Weinig mensen zijn bezorgd over de modellering van
de afvoer van een bad, tenzij deze ongewild zou ontstaan
(bijvoorbeeld door een lek), maar op dezelfde manier zou ook een bad
beheerst kunnen geledigd worden. De afvoer zou dan met een positief
feedback proces kunnen gebeuren: hoe meer water in het bad, hoe
groter de afvoer, hoe minder water in het bad, hoe kleiner de afvoer.
Noteer dat de niet veranderende eenheid een volume is, en dat volume
is relevant voor het bad, de eenheid: het bad heeft een maximaal
en minimaal volume.
We kunnen nu de vier feedback processen door symbolen vervangen:
<<+>> voor (1+k)n, <+> voor -(1+k)n,
<<->> voor (1-k)n en <-> voor -(1-k)n.
Sommen van telkens twee verschillende van deze vier leiden tot zes
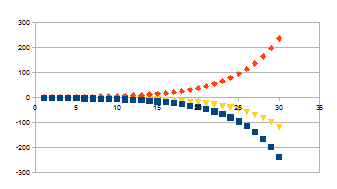
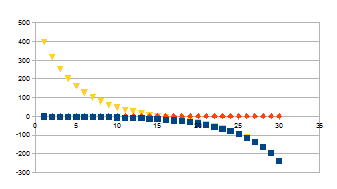
mogelijkheden. In de grafiek is de keuze gemaakt van k=0,2 voor beide
deelaspecten en 30 stappen in het proces. We introduceren hierbij
twee coëfficiënten c1 en c2. We kiezen voor
c1=1 en c2 is zodanig gekozen dat er drie
verbanden te zien zijn op de resolutie van de grafiek: de datapunten
die als driehoek aangegeven zijn geven het gedrag van de uitdrukking
die in de eerste kolom weergegeven is, de datapunten met vierkant en
ruit geven het gedrag van de twee onafhankelijke factoren van die
uitdrukking.
Uitdrukking
|
Grafiek
|
Bespreking
|
1<+>+0,5<<+>>
|
|
Indien beide coëfficiënten gelijk genomen worden is het
resultaat voor elke stap nul. Positieve feedback in de negatieve
zin en positieve feedback in de positieve zin heffen elkaar dan
op.
|
1<+>+500<->
|
|
Dalende S curve, de datapunten van het resultaat bij de hogere
stappen is amper te onderscheiden van de datapunten van <+>
|
1<+>+500<<->>
|
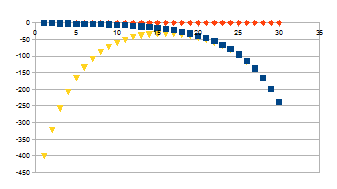
|
U curve met centraal maximum, de datapunten van het resultaat bij
de hogere stappen is amper te onderscheiden van de datapunten van
<+>
|
1<<+>>+500<->
|
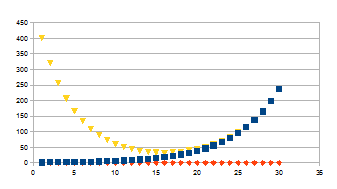
|
U curve met centraal minimum, de datapunten van het resultaat bij
de hogere stappen is amper te onderscheiden van de datapunten van
<<+>>
|
1<<+>>+500<<->>
|
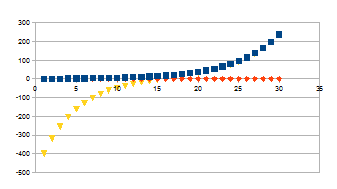
|
Stijgende S curve, de datapunten van het resultaat bij de hogere
stappen is amper te onderscheiden van de datapunten van <<+>>
|
1<->+0,5<<->>
|

|
Indien beide coëfficiënten gelijk genomen worden is het
resultaat voor elke stap nul. Negatieve feedback in de negatieve
zin en negatieve feedback in de positieve zin heffen elkaar dan
op.
|
Behalve de reeds goed gekende patronen van exponentiële toename
en afname worden nu ook een S-patroon en een U-patroon gegenereerd
wanneer de twee elementen van de som ±c1(1±k)n±c2(1±k)n
een tegengestelde karakteristiek hebben, de ene (1+k), de andere
(1-k). Dit zijn de elementen die de dynamiek genereren. Ze modelleren
namelijk de onzekerheid dat wat door het agens geanticipeerd wordt
ook ervaren kan worden, waardoor ze de waarschijnlijkheid modelleren
dat er na n stappen actie ondernomen zal worden door het betrokken
agens.
De twee voorbeelden die geen S-patroon of U-patroon vertonen maken
de interpretatie duidelijk. Wat we modelleren is de intensiteit van
een eenheid die “gevuld” wordt (positieve of negatieve feedback
in de positieve zin) of die “geledigd” wordt (positieve of
negatieve feedback in de negatieve zin). In de voorbeelden wordt het
vullen en ledigen uitgevoerd met een proces met zelfde eigenwaarde.
Enkel voor de twee voorbeelden die geen S-patroon of U-patroon
vertonen kunnen we zeggen dat dit overeenkomt met dezelfde
verdubbelingstijd (respectievelijk halveringstijd) want enkel dan
geeft dezelfde eigenwaarde een zelfde verdubbelingstijd voor een
positieve feedback als voor een negatieve feedback. Het verschil
merken we goed aan de grootte van de coëfficiënten en dit maakt de
volgende interpretatie mogelijk: om het S of U patroon waar te nemen
heeft men een groot verschil nodig van <<de gelijkaardige
(zelfde k) positieve feedback processen>> en <<de
gelijkaardige (zelfde k) negatieve feedback processen>>,
processen die in parallel een entiteit groter of kleiner
maken. Dit maakt dan de volgende interpretatie mogelijk: het product
van eigenwaarden met de coëfficiënten modelleert een aantal
gelijkaardige entiteiten (entiteiten met zelfde eigenwaarde) die
in parallel ageren. Als we twee coëfficiënten onderscheiden dan
zijn beide referentiepunt voor elkaar. Dat betekent dat voor elke
soort entiteit het doel (negatieve feedback) of het anti-doel
(positieve feedback) ook tijdens de loop van het proces kan
veranderen afhankelijk van een aantal gelijkaardige entiteiten die in
parallel ageren. We zullen “gelijkaardige entiteiten” ook als een
soort modelleren en de toename of afname van populaties
die elkaar beïnvloeden kunnen onderzoeken.
De voorbeelden maken ook duidelijk dat S-patroon en U-patroon
enkel op de schaal van de grafiek verschijnen als de negatieve
feedback een grotere intensiteit heeft dan de positieve feedback.
Door variëren van de intensiteit is het mogelijk om een ongeveer
symmetrisch ogende curve te bekomen, toch is de curve, noch naar
links, noch naar rechts, begrensd. De stappen zijn enkel begrensd
door de keuze van start en eind.
Algemeen som gedrag
Beide nieuwe patronen kunnen beter bestudeerd worden door de
relatie verder te veralgemenen. We merken op dat elke genererende
term ±c(1±k)n de intensiteit c is van een som van de
intensiteit n van producten. De eenheid is dan (1±k). De
intensiteit van die eenheid kunnen we in zijn algemeenheid noteren
als ±c(1±k)±d(n±m), inderdaad de som in de exponent
codeert een vermenigvuldiging van een aantal (1±k) elementen. De
sommen (1±k) en (n±m) worden gewogen met een eigen coëfficiënt
(terug een product). Indien we veronderstellen dat bij elke stap ook
de coëfficiënten kunnen variëren, dan is (n±m) ook in de vorm
(1±k) te schrijven. Elk van deze product termen is dan in een vorm
gebracht van een getal dat de rol van intensiteit kan spelen
voor elke operatie (som,
product, machtsverheffing en tetratie), waarbij enkel een
dubbelgetal de kan rol van eenheid spelen voor elk van de
volgende operaties: som, product, machtsverheffing en tetratie. Het
“laatst
toegevoegde getal” vinden we dan in de exponent.
Het S-patroon of het U-patroon wordt enkel gegenereerd door een
keuze van de ki met tegengesteld teken, n en m met
tegengesteld teken, en de coëfficiënt van de exponent met zelfde
teken. Het verschil tussen een S-patroon of een U-patroon wordt
bepaald door het tegengesteld teken (voor S) of het zelfde teken
(voor U) van de coëfficiënten ci. Het teken van de
coëfficiënt in de exponenten bepaalt de richting van het patroon.
De algemene getalmatige relatie van een enkelvoudige combinatie van
spontane gedragingen kunnen we dan voorstellen als
c1(1-k1)f(d-n)-c2(1+k2)g(e-n)
waarin enkel de n gemeenschappelijk is in de twee termen, verwijzend
naar de stap in het globale proces. Het bepalen van acht getallen
(c1, c2, k1, k2, d, e, f,
g) op basis van de waarneming (en dus van de waarde van de feedback
na de anticipatie) maakt het dus mogelijk de relevante (globale) stap
te bepalen in het proces en omgekeerd: de globale stap genereert
minstens 8 (telbare) entiteiten in het proces. De bestudeerde
patronen zijn intensiteiten van dezelfde eenheid. Het is belangrijk
om dit te beklemtonen aangezien we ook kunnen modelleren dat
verschillende soorten (eenheden) elkaar zouden kunnen beïnvloeden.
De afhankelijkheid
van het aantal stappen van een eigen eigenwaarde kunnen we ook
afzonderlijk modelleren en onderzoeken (een aantal entiteiten hebben
dan een veranderende eigenwaarde als bijkomend proces).
S patroon
Als eerste voorbeeld geven we de grafiek die overeenkomt met het
volgende verband: (1-k)f(d-n)-(1+k)f(e-n) in de
loop van de stappen op de horizontale as, waarbij k=0,2 f=1,5 d=35,
e=5 en n tussen 0 en 40. Merk op dat er een quasi lineair verband
bestaat tussen stap 13 en stap 27, de verandering wordt in die
periode (of in dat volume of schaalverschil) blijkbaar in een
duidelijk bepaald gebied gebufferd, het verschil dat een verschil
maakt is amper groter dan de resolutie van de ordinaat as.
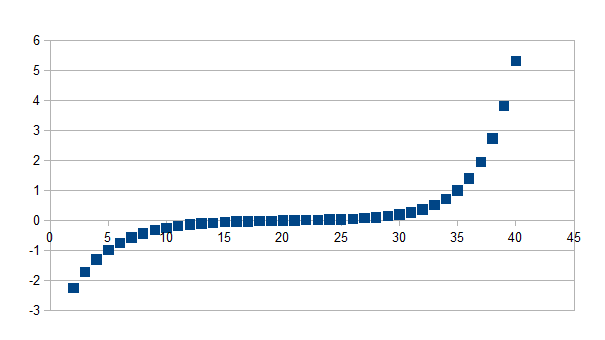
De
S-curve is natuurlijk een duidelijke S of Z bij het wisselen van de
assen.
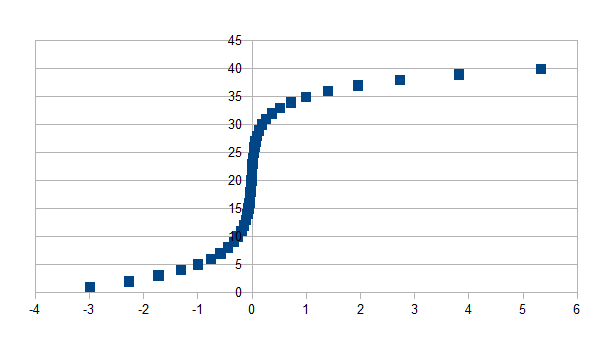
Dit
illustreert ook mooi de dualiteit van tijd of ruimte en de waarneming
van een veranderende intensiteit. We kunnen immers de waarneembare
intensiteiten als tijdstap interpreteren en de tijdstap als
intensiteit en zo wordt duidelijk dat op één moment, tussen het
waarnemen van 0-x en 0+x “plots” een intensiteitstoename bereikt
wordt, of een nieuwe situatie die daarvoor onbereikbaar geacht werd
(niet kon geanticipeerd worden). Hierbij hangt x enkel af van onze
waarnemingsresolutie.
De getalwaarde van d en e zijn gerelateerd aan de getalwaarde van
de stappen dus aan simultaneïteit. Kiest men (voor de gemaakte keuze
van c1 en c2) het gemiddelde van d en e
ongeveer in het midden van het geanticipeerde traject (dus waar in de
voorbeelden de nullijn overschreden wordt) dan genereert dit een
symmetrische curve. Hoe groter het verschil tussen de twee getallen,
hoe kleiner de waarde van de uitdrukking (de intensiteit van het
verschil dat een verschil maakt). De getalwaarde van f, dus de
grootte van het product van eigenwaarden, zal dan de vlakheid van het
centraal gedeelte bepalen: hoe groter f hoe vlakker het centraal
gedeelte, hoe langer dus de intensiteit van het verschil dat een
verschil maakt in een zeer beperkt gebied blijft. Als voorbeeld geven
we de grafiek die overeenkomt met het volgende verband:
(1-k)f(d-n)-(1+k)f(e-n) in de loop van de
stappen op de horizontale as, waarbij k=0,2 f=7 d=45, e=-5 en n
tussen 0 en 40.
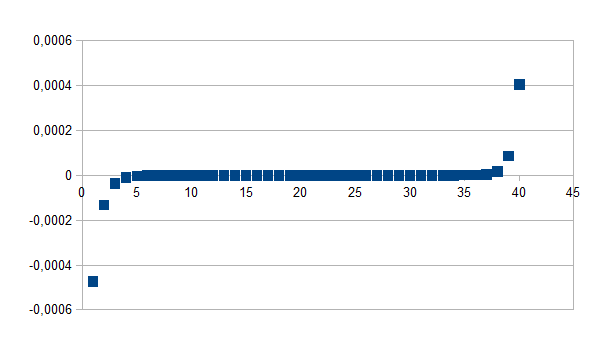
De
omslagpunten zijn hiermee duidelijker weergegeven.
U patroon
Als tweede voorbeeld geven we de grafiek die overeenkomt met het
volgende verband: (1-k)f(d-n)+(1+k)f(e-n) in de
loop van de stappen op de horizontale as, waarbij k=0,2 f=3 d=45,
e=-5 en n tussen 0 en 40.
Uiteraard zijn hier de omslagpunten evenzeer duidelijk.
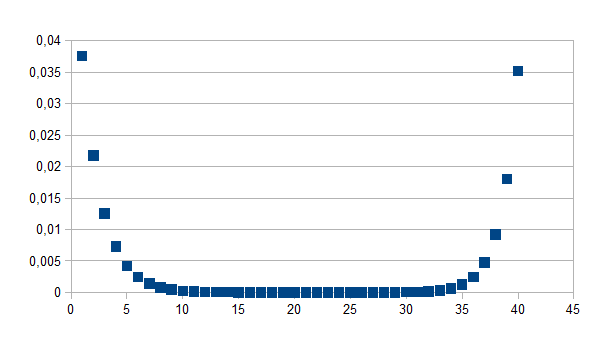
Een S-patroon of een U-patroon wordt dikwijls waargenomen in
spontane processen. Het S-patroon vinden we dikwijls bij een plotse
toename of afname van een parameter in het proces, waarna het proces
op een ander niveau schijnt te stabiliseren (het exponentieel gedrag
wordt goed door een lineair gedrag benaderd). Een U-patroon of
“badkuip kromme” vinden we in een proces dat enkel afwijkend
gedrag aan het begin en aan het einde vertoont zoals bij de
introductie van een nieuw product dat in het begin kinderziekten
vertoont en op het einde niet meer functioneert zoals gewenst.
De stabiliteit gedurende een langere tijd voedt op het eerste
zicht de overtuiging dat het gedrag in een attractor beland is en
hier dus niet weg kan. Er is blijkbaar evenwicht bereikt. Niets
blijkt minder waar te zijn, want hier zijn ook twee omslagpunten of
kantelpunten te zien (“tipping points”) waarbij dat evenwicht
plots verbroken wordt. Die omslagpunten zijn dus anticipeerbaar, ze
hoeven niet het gevolg te zijn van een willekeurige beslissing. Door
deze manier van modelleren als een universeel som gedrag kunnen we
dus modelleren dat sommige processen pas na een zekere tijd
“reageren” op veranderingen. Het zal niet eenvoudig zijn om de
coëfficiënten hiervoor met voldoende grote resolutie te bepalen.
Er zijn veel voorbeelden van omslagpunten en uitgestelde reacties
die verrasten (die niet konden geanticipeerd worden zelfs al
werd vermoed dat ze zouden kunnen waargenomen worden). Pas achteraf
kon er dan een causale betekenis aan verbonden worden. Bijvoorbeeld:
de faseovergang (vast-vloeibaar-gas) van water op het einde
van een vlak stabiel gedrag in de loop van een geleidelijke
toename/afname van moleculaire beweging (warmte)
de plotse magnetisatie als dipolen zich spontaan organiseren
de plotse omslag van een stabiel geachte organisatie naar een
andere vorm (zoals bij het plotse instorten van de Sovjetunie in
1989, de bankencrisis in 2008, of bij de “arabische lente” in
2010) waarbij plots een vicieuze cirkel doorbroken werd van de
wederzijdse beïnvloeding van individuele agentia die geloven dat
andere agentia geloven in de toekomst van die organisatievorm maar
er zelf niet in geloven (en dat terwijl andere agentia geloven dat
de individuele agentia dat wel doen, zich daarnaar gedragen en zo de
indruk geven dat elke individuele agens alleen staat). Dit voorbeeld
laat ook de noodzaak zien van een grote hoeveelheid parallelle
processen om de doelgerichtheid van negatieve feedback de overhand
te kunnen geven in een proces.
het plotse inzicht in het sprookje van Andersen over de
nieuwe kleren van de keizer, toen een kind uitriep dat de keizer
geen kleren aan had (terwijl niemand dat durfde te zeggen omdat
juist niemand anders dat durfde te zeggen). Hier wordt het kind
gebruikt om aan te geven dat het zo moeilijk is om ons iets voor te
stellen zonder duidelijk oorzakelijk verband.
bistabiele schakelaars die pas plots schakelen als er eerst
voldoende energie gebufferd werd
het onvoorspelbare van catastrofale gebeurtenissen, een
plotse emotionele omslag, de verspreiding van “urban legends” en
andere “besmettelijke patronen” (memes), ...
Verder onderzoek
We hebben de som van twee termen onderzocht die enkel als product
te schrijven zijn. Elke term is dus een deelproces, een entiteit die
enkel van intensiteit verandert. Elke term is dus van het type h•g
en is dus een specifieke invulling van een welgevormde
haakuitdrukking met getalcoëfficiënten.
De coëfficiënten modelleren een som van dezelfde eenheid. Het is
dus te verwachten dat elke dynamische anticipatie (die dus een
“indien..., dan..., zoniet...” is) als een
som van vier van deze termen, als minimaal aantal verschillende
eenheden kan geschreven worden waarvan er drie hetzelfde teken
hebben (aangezien dat eveneens geldt voor welgevormde
haakuitdrukkingen die eveneens een “indien..., dan..., zoniet...”
zijn). Het resultaat zal dan kunnen beschouwd worden als een som van
één U-curve (twee maal een positieve coëfficiënt) met één
S-curve (een maal een positieve coëfficiënt, eenmaal een negatieve
coëfficiënt), meer dan deze twee soorten relaties is er niet nodig.





















