De processnelheid is een metrisch begrip dat de relatie kwantificeert tussen twee extrema in een verandering (een proces met een laatst toegevoegde onderscheiding die niet ingebouwd wordt in de tralie). Op basis van deze zeer eenvoudige aanname kunnen we twee elementen onderscheiden: een eenheid met een intensiteit (x-x₀)_(t) waarbij de eenheid (x-x₀) niet verandert (enkel de intensiteit) en een processnelheid k die we een eigenwaarde van het proces genoemd hebben. De intensiteit van de eenheid kan door verschillende processen veranderd worden, processen die in tegengestelde zin werken, die in dezelfde zin werken, en die daarenboven zowel positieve feedback processen als negatieve feedback processen kunnen zijn. We zijn immers altijd in staat een steady state proces te modelleren door een geschikte normalisatie van de intensiteit van elk deelnemend proces. We kunnen ons dan voorstellen dat de grootte van een eenheid door een input proces en een output proces bepaald wordt, waarbij beide processen dus afhangen van de intensiteit van de eenheid zelf. Het input proces heeft een eigenwaarde, het output proces heeft een eigenwaarde. De grootte van de eenheid is dan de grootte van een buffer.

We hebben daarenboven ook begrepen dat de verandering van intensiteit van een entiteit en de verandering van intensiteit van een eigenwaarde door hetzelfde patroon kunnen gegeven worden.

Een volgende stap in het onderzoek van welk gedrag we kunnen modelleren zetten we nu door de eigenwaarde van een deelproces ook afhankelijk te maken van de veranderende intensiteit van een andere entiteit. Dat is een nieuwe stap in de modellering van interagerende processen waarbij een input van het ene een output is van het andere. Bijkomend veronderstellen we dat door een geschikte normalisering de veranderende intensiteit kleiner dan 1 kan gehouden worden om te simuleren dat beide veranderende entiteiten deelprocessen zijn van hetzelfde groter proces.

De intensiteit van het eerste deelproces met eigenwaarde k₁ wordt in zijn algemeenheid gegeven door c₁(1+k₁)^f(d-n).

De intensiteit van het tweede deelproces met eigenwaarde k₂ wordt in zijn algemeenheid gegeven door c₂(1+k₂)^g(e-n).

We kunnen nu k₁ laten afhangen van de intensiteit van het tweede deelproces en dus wordt de intensiteit van het eerste deelproces gegeven door c₁(1+c₂(1+k₂)^g(e-n))^f(d-n).

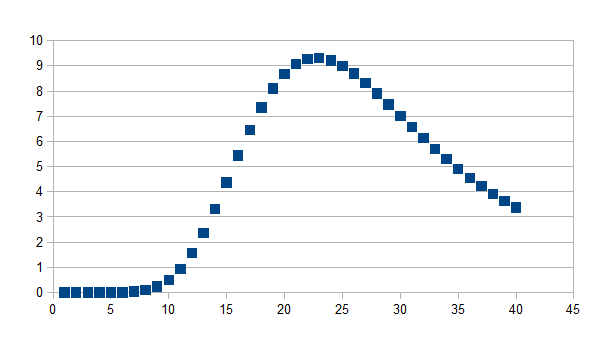
We geven hiervan een voorbeeld met de volgende constanten: c₁=0,5; c₂=-1; k₂=0,01; g=7; e=0; f=1; d=10.

Deze grafiek kunnen we als volgt interpreteren.

Stel dat de waarnemingsresolutie niet groter is dan 1 stap op de ordinaat as, dan is de intensiteit slechts groot genoeg na 11 tijdstappen om een verschil waar te nemen dat een verschil maakt. Rond stap 23 wordt een omslagpunt bereikt.

We kunnen de intensiteiten ook in de abscis weergeven, wat de volgend interpretatie misschien vergemakkelijkt:

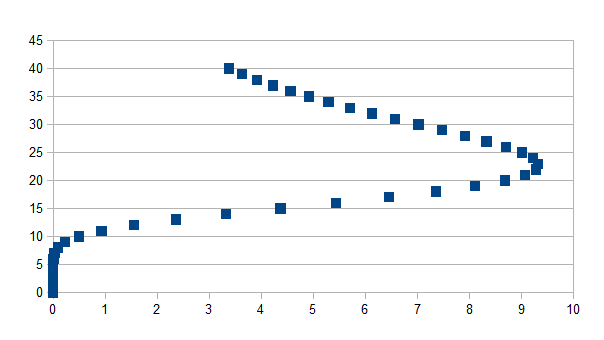
Stel dat we een lijst van intensiteiten hebben, dan is duidelijk dat in de lage intensiteiten er onzekerheid is over wanneer (of op welke schaal) de intensiteit zou waargenomen kunnen zijn, maar een onzekerheid tussen twee stappen blijft (of we dat nu in de grafiek kunnen representeren of niet, er zijn altijd twee schalen die met de waargenomen intensiteit zouden kunnen overeenkomen). Dit kunnen we heel duidelijk maken door de volgende constructie: de relatie tussen stap en waarnemingsintensiteit van een entiteit kan ook door een transformatie van de schaal op de assen getransformeerd worden. De logaritme is een transformatie die één op één is. We nemen de logaritme van de formule m=c₁(1+c₂(1+k₂)^g(e-n))^f(d-n). Dus logm=log(c₁(1+c₂(1+k₂)^g(e-n))^f(d-n)) en dus logm=f(d-n)log(c₁(1+c₂(1+k₂)^g(e-n))=f(d-n){logc₁+log(1+c₂(1+k₂)^g(e-n))}=f(d-n){logc₁+g(e-n)log(1+c₂(1+k₂))}=f(d-n)logc₁+f(d-n)g(e-n)log(1+c₂(1+k₂)) en dit is een kwadratische vergelijking in n. Voor elke m (intensiteit) zullen er dus twee n (stappen) zijn.

logm=f(d-n)logc₁+f(d-n)g(e-n)log(1+c₂(1+k₂))

logm=fdlogc₁-nlogc₁+fglog(1+c₂(1+k₂))(de-dn-en-n²)

logm=fdlogc₁+ fglog(1+c₂(1+k₂))de-(logc₁+d+e)n-fglog(1+c₂(1+k₂))n².

Dit werpt een ander licht op de beperking van een agens om op basis van voor hem te onderscheiden intensiteiten toekomstig gedrag te anticiperen of verleden gedrag te reconstrueren. Hetzelfde verschil dat een verschil maak kan immers waargenomen worden in de toekomst als in het verleden, de inherente beperking van elke waarneming maakt de hypothese van cyclische processen onvermijdelijk.

Dit maakt duidelijk dat rotatie en de inherente beperking van waarneming uitdrukkingen zijn van hetzelfde patroon.

Dit moet het mogelijk maken om op een nieuwe manier hysteresis verschijnselen en bifurcaties te modelleren.

Dit is natuurlijk verder uit te breiden. Met een kubische vergelijking in n en veeltermen met nog hogere machten zouden de verschillende topologische vormen uit de catastrofe theorie (René Thom, Christopher Zeeman 1977) kunnen gemodelleerd worden.