Verschil van welgevormde haakuitdrukkingen

Een gecollapste haakuitdrukking drukt altijd een ervaren uit, en kan altijd door een verschil van twee welgevormde haakuitdrukkingen geconstrueerd worden. We hebben het verschil (y⊕<x>) geconstrueerd van twee (elkaar uitsluitende) toestanden x en y en aangetoond dat dit een noodzakelijke voorwaarde is voor elke toestand, wat we dus de dynamiek genoemd hebben in het ervaren zelf. Het verschil is niet anders als van elke welgevormde haakuitdrukking een zelfde haakuitdrukking afgetrokken of opgeteld wordt, bijvoorbeeld (y⊕<x>)=(y⊕z)⊕<(x⊕z)>. Dit herkennen we als een eigenschap van “snelheid”: een referentiepunt (een aantal toestanden, een bepaald onderscheidingen universum) is willekeurig te kiezen en enkel een verandering hiervan is waarneembaar. Aan een welgevormde haakuitdrukking kan geen “snelheid” verbonden worden, het begrip “snelheid” vereist een verschil.

Ook de referentie toestand speelt een rol. We hebben het verschil gekozen als (y⊕<x>), maar we hadden evenzeer kunnen kiezen voor (<y>⊕<x>). We moeten die keuzevrijheid steeds voor ogen houden. Dit is belangrijk om de volgende reden: het is altijd mogelijk om uit te drukken dat de toestanden x_i dezelfde waarde hebben, hoe uitgebreid we i ook nemen, daarentegen het is niet mogelijk om uit te drukken dat de toestanden x_i tegengestelde waarde hebben, dat kan enkel voor twee toestanden. Hoe dan ook zijn er twee referentie toestanden: y en <y>.

We kunnen ook verschillen van verschillen van toestanden construeren en we hebben dat generaties genoemd. De intensiteit van een atoom kunnen we modelleren door het product van twee verschillen uit de eerste generatie en ook door het product van een verschil uit de eerste en de tweede generatie (maar niet door een product van twee verschillen uit de tweede generatie).

Het verschil (y⊕<x>) is als klassieke vector (projector) uit te drukken en is niet anders dan een gewogen projector van een afgeleide bijvoorbeeld (y⊕<x>) is niet verschillend van x•(<>⊕x•y). De afgeleide is een welgevormde haakuitdrukking, en dus is het aspect “snelheid” niet van toepassing op de afgeleide x•y. Maar (<>⊕x•y) kunnen we wel de betekenis geven van een klassiek vectoriële (gerichte) snelheid aangezien (<>⊕x•y) een projector is (de identiteitstransformatie voor zijn ruimte en gezien de speciale eigenschappen van projectoren). Dus de eenheid (<>⊕x•y) kunnen we hanteren als een snelheidseenheid die een intensiteit kan hebben, eenheid die simultaan is met twee toestanden. We moeten dus voorzichtig zijn met de connotaties die men aan het begrip “snelheid” verbindt. Daarom gaan we het abstracte begrip “snelheid” nu onderzoeken als “processnelheid” met de bedoeling om ook een verandering van “onvermijdelijke verandering” te kunnen modelleren.

Processnelheid is abstracter dan snelheid

Voor sommige processen (“veranderingen in de tijd”, maar zoals we zullen aantonen ook veranderingen in resolutie) kunnen alle mogelijke toestanden (al dan niet atomen) geanticipeerd (of gereconstrueerd) worden. Anticipatie (of reconstructie) verwijst naar de potentialiteit die we modelleren. Een proces dat meer van die geanticipeerde (gereconstrueerde) toestanden bereikt heeft is sneller dan een proces dat minder van die geanticipeerde (gereconstrueerde) toestanden bereikt of doorlopen heeft. Het gebruik van de begrippen “meer” en “minder” duidt er op dat we dan iets zouden kunnen kwantificeren als we een eenheid zouden vinden. Vanuit het inzicht dat uit het onderzoek naar dynamiek ontstaan is en hierboven herhaald werd, is dit het aantal onderscheidingen in een simultaneïteitsinterval en is de eenheid (<>⊕x•y). Het is dat kwantificeerbaar verschil dat zowel aan het begrip “rotatie”, als aan het begrip “processnelheid” betekenis geeft. Dit begrip moeten we nu heel precies modelleren omdat de keuze van een naam voor het abstracte inzicht niet vanzelfsprekend is wanneer we a priori willen vermijden. Inderdaad:

1. behalve voor voorbeelden hebben we nergens het begrip “tijd” moeten gebruiken, we hebben het vervangen door het begrip “elkaar uitsluiten” en bijvoorbeeld ook “punten in de fysische ruimte” sluiten elkaar uit.

2. de afstand tussen twee toestanden in hetzelfde onderscheidingen universum kan onmogelijk in één dimensie uitgedrukt worden, maar kan, zoals alle welgevormde haakuitdrukkingen op een unieke manier in twee dimensies gekwantificeerd worden. Een afstand is metrisch en is geordend. Binnen één dimensie is die ordening strikt.

3. “dynamiek” hebben we gerelateerd met de intensiteit van een laatst toegevoegde onderscheiding, en die kan al dan niet ingebouwd worden in de tralie die het agens kan hanteren om zijn werkelijkheid op te spannen. Wordt de laatst toegevoegde onderscheiding ingebouwd, dan gebeurt dit onvermijdelijk ook in een toestand.

Een verschil van toestanden is een noodzakelijke voorwaarde voor elke toestand en het is dat verschil dat we nu “processnelheid” noemen: het verschil dat onvermijdelijk niet kan onderscheiden worden van “een ervaren”. Door processnelheid te kwantificeren, kwantificeren we dynamiek.

Classificatie van processnelheid

We onderscheiden nu drie mogelijkheden: een processnelheid nul, een maximale (minimale) resolutie en een meetbare processnelheid.

Processnelheid nul

De snelheidseenheid (<>⊕x•y) is niet verschillend van de nul vector voor x=y. Dan is een van de extrema eveneens niet verschillend van de nulvector (want (y⊕<x>) is niet verschillend van X). Het is dus enkel de som (en het dus begrip projector) die “een processnelheid gelijk aan nul” betekenis geeft en dit volgt rechtstreeks uit simultaneïteit. Dan speelt de laatst toegevoegde onderscheiding zijn rol als volgt in het interval: A=(x⊗X)_ℵ=<x>⊕<ℵ•x>=x•(<>⊕<ℵ>)=ℵ•x•(<>⊕<ℵ>). In dat geval is de commutator A⊕<A^-1> die dus niet anders is dan <ℵ•x>⊕<ℵ•y> gelijk aan ℵ•x en gelijk aan ℵ•y, en geeft daarmee duidelijk de grootte van het universum (de bitstring van x en van y moet een aantal maal herhaald worden om uitdrukbaar te zijn in het momentaan laatste en grootste universum).

Indien de eenheid van processnelheid nul is geeft de commutator de grootte van het universum.

We beschikken dan over een interval tussen X en x (of tussen X en y) en dat zijn de twee extrema waarbij dus de waarde van x (en dus ook y) niet gekend is. Het interval heeft het karakter van een gewogen projector, de projector van de laatst toegevoegde onderscheiding die daardoor een ervaren uitdrukking is. Een concreet voorbeeld hiervan is dat de (uiteraard vectoriële) snelheid nul is wanneer het ervaren van x ook het ervaren van y impliceert, x en y hebben dan dezelfde waarde <> en het zijn dus geen elkaar uitsluitende toestanden. Een snelheid gelijk aan nul is natuurlijk ook mogelijk voor twee elkaar uitsluitende toestanden (en daarvoor is het voldoende dat één van de toestanden ervaringswaarde <<>> heeft) maar dan met de extra veronderstelling dat beide ervaringswaarde <<>> hebben. Inderdaad: veronderstel dat x de waarde <<>> heeft en dat y de waarde <<>> heeft, dan sluiten ze elkaar uit (hun conjunctie heeft de waarde <<>>) en er geldt ook dat de afgeleide x•y de waarde <<>> heeft en dus dat de snelheid (<>⊕x•y) niet onderscheiden kan worden van de nulvector. Dit is het geval bij simultaneïteit in het gebeuren (wanneer het laten gebeuren van x ook het laten gebeuren van y impliceert, x en y hebben dan evenzeer dezelfde waarde). De processnelheid is dus nul als de toestanden simultaan zijn, en dat moeten we dubbel interpreteren, zowel elkaar insluiten als elkaar uitsluiten. Maar het begrip is nog abstracter: de processnelheid is nul als twee toestanden dezelfde waarde hebben, waarde die verder niet gekend is.

Nul kunnen we operationeel interpreteren als waarneembaar willekeurig klein en daarenboven onwaarneembaar nog kleiner. In deze interpretatie vinden we ook dat de standaard taal de ordening uitdrukt die aan de basis ligt van simultaneïteit. Door het gebruiken van “nul” kunnen we de (gekozen of niet gekozen) onmogelijkheid van (het waarnemen van) ordening uitdrukken.

Resolutie

We merken nu op dat het centraal axioma zegt dat we altijd iets ervaren en dat dit niet onderscheiden kan worden van iets anders dat gebeurt. Dus, “we ervaren hoe dan ook altijd iets” is niet anders dan de veronderstelling dat een van beide toestanden de waarde <> heeft. De andere toestand moet dan waarde <<>> hebben, want stel dat die toestand geen waarde zou hebben dan kan niet uitgedrukt worden dat beide toestanden elkaar uitsluiten. In het ervaren zelf hebben de beide toestanden dus een tegengestelde waarde, en juist dat is het andere extreem geval, dus x•y=<> of x en y hebben tegengestelde waarde. “Tegengestelde waarde hebben” is een unieke situatie voor twee toestanden (want het is niet uit te drukken voor meerdere toestanden). In dat geval is (x⊗(y⊕<x>))_ℵ=<y>=x, de extrema van het interval zijn niet te onderscheiden (er zijn geen twee verschillende toestanden) behalve voor het symbool dat we eraan toekennen en de snelheidseenheid <>⊕x•y is niet verschillend van <<>>. Hierbij moeten we opmerken dat de intensiteit van <<>>=(<<>>⊗<<>>)_ℵ, die gegeven wordt door ℵ zowel zeer groot als zeer klein kan zijn, maar verschillend van nul (is de intensiteit groot dan is de inverse van de intensiteit klein). ℵ codeert immers het grootste universum waarin de welgevormde haakuitdrukkingen moeten uitgedrukt worden, en de lengte van de vectoren en de grootte van dat universum is als de binaire logaritme van de som van de kwadraten van de bits te berekenen. Dit is dus een getal en dus meetbaar. Hetzelfde getal ℵ vinden we bij de twee toestanden terug, namelijk (x⊗x)_ℵ=x en (<y>⊗<y>))_ℵ=<y>. Dit kunnen we niet anders interpreteren als dat de twee punten elkaars inbedding zijn want <y>=x dus y=<x> en <<x>>=x. In dat geval is de commutator A⊕<A^-1>, die dus niet anders is dan <ℵ•x>⊕<ℵ•y>, gelijk aan de nul vector.

De eenheid van processnelheid geeft de grootte van het universum en de commutator is nul.

Merk dat dualiteit ingebakken zit in het concept “processnelheid”. De projectieve snelheidseenheid <>⊕x•y gelijk aan <<>> met een bepaalde intensiteit gegeven door ℵ kan dus geen verandering modelleren maar geeft wel de waarde van de grootte van het onderscheidingen universum (voor twee toestanden die elkaars inbedding zijn) op dezelfde manier als bij de processnelheid gelijk aan nul (voor twee toestanden die zich niet onderscheiden van elkaar). De maximale (minimale) grootte van een onderscheidingen universum interpreteren we als de maximale (minimale) resolutie die door het agens-in-context kan gerealiseerd worden, dus de maximale (metrische) afstand tussen twee punten die altijd de afstand is tussen de twee punten die elkaars inbedding zijn. De maximale (minimale) waarde van de eenheid van de processnelheid, namelijk <>⊕x•y=<<>>, is dus gegeven door de maximale (minimale) resolutie die mogelijk is om een onderscheid te maken tussen twee extrema die elkaar inbedding zijn en dus maximaal (minimaal) verschillen. Dit is agens-in-context gebonden.

Maar nu dringt zich nog een tweede interpretatie op want <<>> is de tweede afgeleide naar ℵ. De tweede afgeleide geeft het punt dat simultaan is met de verandering (het proces) van de snelheid en dus ook een processnelheid. De processnelheid is in het onvermijdelijke geval van een interval tussen twee toestanden die elkaars inbedding zijn dus een versnelling (want dit begrip begrijpen we als “de verandering van een snelheid”, snelheid die ook als processnelheid gemodelleerd is, dus “de processnelheid van een processnelheid”). In een ervaren toestand is processnelheid dus onontkoombaar en heeft een maximale (minimale) numerieke waarde: de grootte van het onderscheidingen universum dat in een bepaalde ervaren toestand nodig en voldoende is om de toestand ten opzichte van een andere toestand te onderscheiden.

Hier herkennen we wat in de algemene relativiteitstheorie zonder verklaring moet aanvaard worden: aan versnelling is niet te ontsnappen, aan een onderscheidingen universum met een bepaalde grootte is niet te ontsnappen. Als we dan een referentie nodig hebben dan is het altijd mogelijk om de lokale spontane versnelling (“de vrije val”) als referentie te gebruiken. Maar deze inzichten moeten natuurlijk nog verder onderbouwd worden eens we de onderliggende begrippen goed begrepen hebben. We zullen in staat zijn fysische afstanden en krachten te modelleren en dan zullen we zien dat sommige krachten onvermijdelijk omgekeerd evenredig moeten zijn met het kwadraat van een afstand zoals dat gekend is bij de gravitatie en de elektrische kracht.

Processnelheid meetbaar

We hebben dus een duidelijk getal ℵ als een processnelheid die nul kan zijn en geen verandering kan modelleren, en die maximaal (minimaal) kan zijn en evenmin verandering kan modelleren. We kunnen dan altijd veronderstellen dat de relaties nog wel associatief, maar niet commutatief zijn voor een waarde van de klassieke vectoriële snelheid die niet extremaal is (dus die niet maximaal of die niet minimaal is) en verschillend van nul. Juist dat wordt gemodelleerd door een fractie van de maximale (minimale) intensiteit van de afgeleide. In de fractie herkennen we de deling, en de operatie van delen is niet commutatief.

Verschillen van nul herkennen we in de de commutator. Dat betekent dus dat we veronderstellen dat de commutator minimaal afwijkt van nul (onafhankelijk of we het extremum maximaal of minimaal veronderstellen) gemeten in een begrensde eenheid, maximaal of minimaal gegeven door het grootste onderscheidingen universum dat twee extrema met elkaar kan verbinden en die we kunnen interpreteren als het onvermijdelijke “momentane maximale (of minimale) verschil of dus processnelheid”. Dat betekent dus dat we moeten veronderstellen dat er een kleinste (grootste) verschil moet zijn dat zorgt voor de niet-commutativiteit en dus voor de ordening (“in de tijd” of “in de ruimte”) die geïntroduceerd wordt door ℵ, en dat dit kleinste (grootste) verschil de actuele, momentane, “processnelheid” moet zijn. Dat betekent dus dat we kunnen veronderstellen dat k(ℵ•(<x>⊕<y>)) een zinvolle uitdrukking is met k een reële getalwaarde tussen 0 en 1 (die dus als de intensiteit van een minimale eenheid kan functioneren). Het extremale wordt enerzijds gegeven door k=1, en anderzijds door k=0, die de snelheidseenheid (<>⊕x•y) geeft die niet verschillend is van de nul vector (en dus x=y). De uitdrukking k(ℵ•(<x>⊕<y>)) moet gelezen worden als een disjunctie met de meetbare eenheid (ℵ•(<x>⊕<y>)) en dus invariant voor de transformaties van de tralie opgespannen door ℵ, x en y, minimaal dus drie welgevormde haakuitdrukkingen. Merk op dat de meetbare eenheid bepaald wordt door zowel x als y en geprojecteerd wordt in het grootste onderscheidingen universum die de x en de y met elkaar laten combineren. Merk op dat ℵ•(<x>⊕<y>) perfect uitdrukt welke impact de grootte van het universum heeft waarin ℵ uitgedrukt wordt, grootte van een universum dat ons enkel kan gebeuren en waar we maar gedeeltelijk kunnen voor kiezen. Inderdaad, wat ook het universum is waarin x of waarin y moeten uitgedrukt worden, het is het vectorproduct met ℵ dat het universum van ℵ opdringt aan de andere. We zijn daarenboven van de veronderstelling uitgegaan dat x en y elkaar uitsluitende toestanden zijn. Dat betekent dat hun conjunctie niet verschillend is van <<>>, dus dat <>⊕<x>⊕<y>⊕x•y=<<>>, of dus <x>⊕<y>=<>⊕<x•y>, dus ℵ•(<x>⊕<y>) kan ook geschreven worden als ℵ•(<>⊕<x•y>). Het vectorkwadraat van de commutator ℵ•(<x>⊕<y>) is (<>⊕<x•y>) aangezien de projector idempotent is. Dit geeft dus de eenheid. Noteer dat uit <x>⊕<y>=<>⊕<x•y> ook volgt dat x⊕y=<<>>⊕x•y en dus (<>⊕x)⊕(<>⊕y)=<>⊕x•y, een som van de projectoren van de uitsluitende toestanden is de projector van de afgeleide naar ℵ van het simultaneïteitsinterval (x⊗y)_ℵ. We hebben ℵ reeds als een eenheid geïnterpreteerd en het is deze invariant die ook optreedt als disjunctie met <<>>, dus k<<>> is niet verschillend van k•ℵ.

Hiermee correleren we een scalair aan een simultaneïteitsinterval dat geordend wordt door de haakrelaties tussen ℵ, x en y. We hebben bewezen dat ℵ zich bevindt tussen x en (y⊕<x>) en we kunnen het spoor van ℵ dus interpreteren als de intensiteit k van de eenheid <<>> die ook de eenheid (<>⊕<x•y>) kwantificeert in een universum waarin de nulvector gedefinieerd is. Door het feit dat we 0<k<1 kiezen is het getal k een minimaal getal (en dus is k^-1 een maximaal getal) dat begrensd is door het aantal onderscheidingen van het grootste universum dat zich in ℵ manifesteert. Het is het aantal onderscheidingen waarmee twee toestanden van elkaar verschillen dat de waarnemingsresolutie kan genoemd worden van het agens-in-context dat het proces meemaakt en dus minstens gelijk is aan 1. Het getal k modelleert de intensiteit van verandering, dus de processnelheid die inherent is aan het simultaneïteitsinterval tussen een toestand en het verschil met een andere toestand inherent aan de waarnemingsresolutie van het agens-in-context. Het is een momentane intensiteit, en als dit verandert kunnen we spreken van een versnelling en die verwijst dus naar de grootte van een onderscheidingen universum, en die heeft dan een onvermijdelijk minimum, namelijk 1, minstens 1 onderscheiding moet gemaakt worden.

We merken op dat het duale verschil (en dus het duale simultaneïteitsinterval) tot exact dezelfde voorwaarden leidt: x•y=<> en x•y=<<>> gelden onafhankelijk welke waarde aan x of aan y toegekend wordt. We kunnen dit ook herkennen als volgt: de commutator ℵ•(<x>⊕<y>) kan ook geschreven worden als <ℵ>•(x⊕y) en x=(x⊗x)_ℵ=(x⊗x)_<ℵ>. Dit betekent dat we altijd kunnen veronderstellen dat A=(x⊗(y⊕<x>))_ℵ de “richting” codeert waarin het interval doorlopen wordt. Inderdaad, <A>=(<x>⊗(<y>⊕x))_ℵ=((y⊕<x>)⊗x)_<ℵ> en A^-1=((y⊕<x>)⊗x)_ℵ. De redenering kan volledig duaal opgebouwd worden door de eenheden (<>⊕<x•y>) en (<>⊕x•y) te wisselen en dus te veronderstellen dat x en <y> elkaar uitsluiten.

Merk op dat x en y die elkaar uitsluiten, waarbij een van beide ervaren is, de meest eenvoudige tralie vormen: een 1-splitsing.

Totale ordening

We hebben al begrepen dat een simultaneïteitsinterval kan uitgebreid worden met verschillende tussenliggende punten, wat bijvoorbeeld voor twee tussenliggende punten tussen p en q de uitdrukking oplevert: <<<p>x₁><<x₁>x₂><<x₂>q>>. Dit interval vertoont dus een totale ordening zoals bij de reële getallen, ordening die een “indien... dan...” constructie is met punten die zich tussen de extrema bevinden. In het interval is x₁ groter dan x₂ (indien x₁ dan ook x₂), en dus is x₁ een conjunctie van meer onderscheidingen met dezelfde waarde. Daarom kunnen we ons voorstellen dat sommige verschillen meer simultaan zullen doorlopen worden dan andere naargelang men meer tussenliggende punten kan veronderstellen (anticiperen) en daarom meerdere onderscheidingen moet kunnen inzetten. Daarom kan men altijd een continu doorlopen pad veronderstellen van tussenliggende toestanden (die misschien enkel geanticipeerd kunnen worden, of gereconstrueerd, maar niet waargenomen zullen worden). Deze veronderstelling werd zeer duidelijk 2500 jaar geleden geïllustreerd door Zeno van Elea in de paradox van Achilles en de schildpad. Zeno wou hiermee het idee van “veelheid” bekampen door de “ondeelbare eenheid” te illustreren aan de hand van de volgende redenering: Achilles haalt natuurlijk de schildpad in, hoezeer je ook de afstand die zij afleggen in deelafstanden zou gaan opsplitsen. Immers: per tijdseenheid (per waargenomen verschil van elkaar uitsluitende toestanden) legt Achilles een grotere afstand af dan de schildpad wanneer de afstand gemeten wordt in eenheden die voor de schildpad relevant zijn. Of nog anders uitgedrukt: de eenheden die voor de schildpad relevant zijn, zijn niet relevant voor Achilles, Achilles hanteert een andere “ondeelbare eenheid”. Achilles heeft enkel voordeel in een bepaald soort wedstrijd. We kunnen dit zelfde immers ook illustreren met de waarneming dat het afhankelijk is van de context van de wedstrijd wie zal winnen, bijvoorbeeld: Achilles zal zeker verliezen indien het een wedstrijd zou zijn voor de meest precieze beweging wanneer de variaties gemeten worden in eenheden die voor de schildpad relevant zijn. De veronderstelling van tussenliggende punten die niet waargenomen zullen worden wordt ook geïllustreerd door de waarnemingsparadoxen als gevolg van de continuüm hypothese. Snelheid is dus een meer fundamenteel begrip dan de termen “a” en “tijdseenheid” uit de uitdrukking “(a) per (tijdseenheid)”. Tot deze conclusie zijn we ook gekomen bij de studie van het vermenigvuldigen en delen van getallen en het heeft het mogelijk gemaakt om het begrip “schaalfactor” in het haakformalisme te introduceren. (Proces)snelheid is onvermijdelijk en agens-in-context afhankelijk. We kunnen dit inzicht ook als volgt verwoorden: het is de onvermijdelijkheid van de constructie van een tijdseenheid en een richtingseenheid a (voor een agens-in-context die elkaar uitsluitende toestanden onderscheidt) die zich voordoet als “<<a>> per <<tijdseenheid>>”. We moeten dat interpreteren als “<<a>> per <<processtap>>”. Zowel de a als de tijdseenheid zijn dus aan elkaar gerelateerde maar afgeleide begrippen van het centraal begrip “snelheid” of “schaalfactor”. Dit wordt ook geïllustreerd in de relativiteitstheorie waarin de beide eenheden in elkaar omgezet worden door delen of vermenigvuldigen met een constante snelheid (namelijk x=ct) die we de lichtsnelheid c noemen en die ook als de maximale (minimale) resolutie beschouwd wordt van informatie overdracht door onze zintuigen, resolutie die door de grootte van een onderscheidingen universum gemeten wordt.

Stel dat we k niet als een constant getal beschouwen maar als een valuatie beschouwen van een getalfunctie κ, dan is k de momentane waarde van de tweede afgeleide naar ℵ van een gecollapste haakuitdrukking <y>⊕ℵ•x⊕ℵ•y (tweede afgeleide die altijd een waarde <<>> heeft, in dit geval dus gewogen door k). Dus als we k niet als constant getal beschouwen modelleren we ook de verandering van een momentane versnelling in het haakformalisme, dus de verandering van “de verandering inherent aan het verschil tussen twee waarneembare toestanden”, versnelling die door de maximale (minimale) resolutie begrensd wordt.

Merk op dat het simultaneïteitsinterval A=<y>⊕ℵ•x⊕ℵ•y, als ℵ een rol van eenheid speelt, kan geschreven worden als <y>⊕kℵ•(x⊕y) en dus <y>⊕λ(x⊕y) met 0<λ<1 en λ(x⊕y) een disjunctie waarbij λ de intensiteit is van de <<>> van het momentaan universum. Met λ=0 is dit niet anders dan <y>, met λ=1 is dit niet anders dan x. Als x en y elkaar uitsluiten is dat niet verschillend van <y>⊕λ(<<>>⊕x•y) met 0<λ<1 (want <>⊕<x>⊕<y>⊕x•y=<<>>). Dit is de som van een “punt” en een gewogen projector. Het invers ten opzichte van ℵ wordt dan gegeven door <y>⊕λ(<<>>⊕x•y) met -1<λ<0. Dit alles kunnen we begrijpen als een voorbeeld van de kracht van de klassieke hypothese.

De gecollapste haakuitdrukking <y>⊕ℵ•x⊕ℵ•y kunnen we ook schrijven als (y⊕<x>)•(<>⊕ℵ)⊕x•(<>⊕<ℵ>) in de basis van ℵ. Dus x en (y⊕<x>) zijn de coëfficiënten in die basis. Dus is het simultaneïteitsinterval (x⊗(y⊕<x>))_ℵ de 1-de divergentie-splitsing (x, (y⊕<x>)). De eenheid van de processnelheid bekomen we door het product van beide coëfficiënten te nemen, namelijk x•(y⊕<x>), dit maakt duidelijk dat de eenheid van processnelheid op een factor na bepaald is, inderdaad ook de coëfficiënten C•x en C•(y⊕<x>) zullen tot dezelfde snelheidseenheid leiden. Als C, x en y orthogonale projectoren zijn dan is dit product niet verschillend van de vectorsom en dat herkennen we natuurlijk als de onbepaaldheid van een primitieve in zijn interpretatie als integraal.

Het is de divergentie-splitsing die hierbij optreedt die de verantwoording geeft voor de metriek in de klassieke hypothese.

Voorbeeld

Uitwendige kwantificering

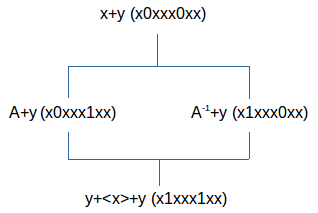
We werken het voorbeeld uit dat we gebruikt hebben om dynamiek te illustreren. We hebben daar twee toestanden verondersteld (elkaar uitsluitende welgevormde haakuitdrukkingen) x als 1100 en y als 0111 (uitgedrukt in een twee onderscheidingen universum). Als laatst toegevoegde onderscheiding ℵ nemen we een vorm die slechts één onderscheiding bijvoegt, namelijk 11110000. Dus ℵ•x wordt uitgedrukt door 11000011 (en de bitstring van x moet daarvoor éénmaal herhaald worden). Dus (y⊕<x>) is 01110111⊕00110011 = 1x001x00.

De som met de referentie toestand levert de volgende tralie op:

Dit is een gecollapste tralie van één onderscheiding (slechts twee betekende bits op dezelfde positie). Dit is in termen van de projector (<>⊕x•y) (som van de elkaar uitsluitende toestanden) niet anders dan

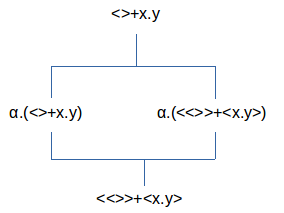
De simultaneïteit van (<>⊕x•y) en dus ook (<<>>⊕<x•y>) is duidelijk te zien. Centraal zien we ℵ•(<>⊕x•y) en <ℵ>•(<>⊕x•y). Dit is niet anders dan ((<>⊕x•y)⊗(<<>>⊕<x•y>))_ℵ en ((<<>>⊕<x•y>)⊗(<>⊕x•y))_ℵ.

De kwantificering met 0<λ<1 enerzijds en -1<λ<0 anderzijds is een invariant voor de tralie met enkel (<>⊕x•y) en (<<>>⊕<x•y>).

Merk op dat y een welgevormde haakuitdrukking is. Een speciaal geval hiervan is <<>> en dus kunnen we ook schrijven dat κ=(A⊕<<>>)_(t+Δt)/(A⊕<<>>)_(t). In dat geval is A⊕<<>>=<ℵ>•(<>⊕<x>) voor elke A. De factor κ kan dan geïnterpreteerd worden als de verhouding van de intensiteit (de coëfficiënt) van de projector (<>⊕<x>) tussen twee onderscheiden stappen en dus zijn lengte. Merk op dat we nu niet meer moeten veronderstellen dat x een toestand zou zijn want de conjunctie van elke x en <<>> is <<>>, ze sluiten elkaar dus altijd uit.

Inwendige kwantificering

De divergentie-splitsing stellen we in zijn meest eenvoudige vorm voor als:

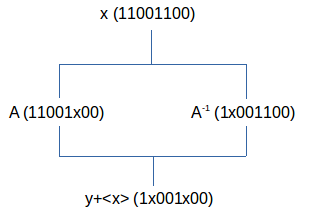
De vier punten hebben zes invariante bits en de twee punten op centraal niveau hebben maar één don’t care. We kunnen dus een kwantificering uitrekenen (die een functie is van het aantal bits van de tralie en dus geen invariant is voor de tralie) met behulp van de inwendige discriminatie intensiteit van elk van deze vier punten met zichzelf.

<x|x>=p²₈+p²₇+p²₆+p²₅+p²₄+p²₃+p²₂+p²₁

<A|A>=p²₈+p²₇+p²₆+p²₅+p²₄+0+p²₂+p²₁

<A^-1|A^-1>=p²₈+0+p²₆+p²₅+p²₄+p²₃+p²₂+p²₁

<y⊕<x>|y⊕<x>>=p²₈+0+p²₆+p²₅+p²₄+0+p²₂+p²₁

Dit zijn 4 vergelijkingen met 3 onbekenden, namelijk de som van de zes invarianten: p²₈+p²₆+p²₅+p²₄+p²₂+p²₁, en de intensiteiten p²₇ en p²₃. Van de vier intensiteiten zijn <A|A>, <A^-1|A^-1> en <y⊕<x>|y⊕<x>> intensiteiten in een ervaren standpunt. De intensiteit van <x|x> kunnen we natuurlijk gebruiken als normalisatie zodanig dat deze intensiteit gelijk is aan 1. De genormaliseerde intensiteiten <A|A>/<x|x>, <A^-1|A^-1>/<x|x> en <y⊕<x>|y⊕<x>>/<x|x> zijn dan fracties van 1.

We kunnen nu ook eens een voorbeeld geven van een laatst toegevoegde onderscheiding die in een groter universum moet uitgedrukt worden. We nemen daarom als laatst toegevoegde onderscheiding 1111111100000000 dan is duidelijk dat de divergentie-splitsing ook de volgende simultaneïteitsrelatie kent:

De sommen worden nu wat uitgebreider, maar het patroon is hetzelfde.

In principe zouden beide kwantificeringen dezelfde informatie coderen. Dit moet nog uitgewerkt worden.

Simulatie

Al deze inzichten kunnen we nu in een praktische vorm gieten die een simulatie mogelijk maakt van opeenvolgende ervaren toestanden. Inderdaad, we beschouwden in het onderzoek naar processnelheid elkaar uitsluitende toestanden die elkaar opvolgen x₀, x₁, x₂,.... Bij het ervaren van deze toestanden hebben de toestanden een ervaringswaarde. Die is waar te nemen als de intensiteit van een eenheid, minimaal een ja voor iets maar misschien wel een intensiteit κ₀, κ₁, κ₂.... In het ervaren zijn ze dus niet verschillend van de onderzochte gecollapste simultaneïteitsintervallen A₀, A₁, A₂,.... Dus een voortschrijdend proces is als een opeenvolging van “A intervallen” waarneembaar, elk met een eigen intensiteit. De intervallen zijn van het type A=<y>⊕ℵ•x⊕ℵ•y en kunnen we ook schrijven als de opeenvolging van verschillen van die intervallen met een vaste referentie toestand y (bijvoorbeeld een begintoestand, dus de toestand van een niet gestart proces), dit zijn dus “A⊕y intervallen”, met A⊕y=ℵ•x⊕ℵ•y, elk met een eigen intensiteit. We kunnen nu een andere naam geven aan y, bijvoorbeeld A₀, want y is de referentie toestand (begintoestand) en het proces is nog niet begonnen. We kunnen dat simuleren door een proces waarvan we veronderstellen dat ℵ niet anders is dan de nulvector X, dus dat A=<y>⊕X•x⊕X•y=<y>. Dus wat we waarnemen zijn “A⊕A₀ intervallen” waarbij enkel A de variabele is, elk met een eigen intensiteit. Als een proces loopt dan is dit interval nooit gelijk aan de nulvector. Het proces is niet anders dan een opeenvolging van “κ_i(<<>>⊕x•A₀) intervallen” waarbij κ_i de intensiteit is van de anderspotente projector of vectoriële eenheid (<<>>⊕x•A₀) en dus (x⊕A₀), eenheid die door twee vaste extrema gedefinieerd is.

De starttoestand A₀ is de enige (onvermijdelijk) die vrij gekozen is, de toestand x is onbekend maar sluit de gekozen toestand uit die niet verschillend is van het simultaneïteitsinterval A₀, en bepaalt samen met die starttoestand de richting van het simultaneïteitsinterval. Dus is ook de eenheid (x⊕A₀) onbekend. Toch kunnen we de intensiteiten van de “A⊕A₀ intervallen” recursief berekenen (een totaal geordende proces) door de volgende procedure om elkaar opeenvolgende intensiteiten te berekenen uitgaande van de beschikbare informatie in een gekozen begintoestand: (A⊕A₀)_(t+Δt)=κ(A⊕A₀)_(t) met -1<κ<+1. Hierbij krijgt het bekende en gekozen simultaneïteitsinterval (de gekozen resolutie, het minimale verschil tussen twee elkaar uitsluitende toestanden) als symbool A₀ en het onbekende simultaneïteitsinterval als symbool A. De parameter κ kan zowel constant als variabel zijn en geeft de intensiteit (product niet verschillend van disjunctie) van het simultaneïteitsinterval. Indien κ=0 dan is er geen verandering. Indien κ negatief is dan is er bij elke stap een vermindering van het verschil met de referentie. Indien κ positief is dan is er bij elke stap een toename van het verschil met de referentie. Hierbij zijn t en Δt geen absolute waarde (zoals de meeste mensen intuïtief tijd begrijpen) maar afhankelijk van de karakteristieken van het proces. Ze zijn afhankelijk van de inherente onderscheidbaarheid van de eenheid A⊕A₀ voor een bepaald agens in een bepaalde context, het is die eenheid die we de waargenomen entiteit noemen en aanleiding geeft tot toestanden die elkaar uitsluiten. Hierbij gebruiken we Δt als het symbool voor de resolutie van de stappen. We schrijven nu κ=(A⊕A₀)_(t+Δt)/(A⊕A₀)_(t). De intensiteit κ meet hoe groot de telbare verhouding is tussen de intensiteiten van het verschil van twee verschillende simultaneïteitsintervallen (dat is dus het verschil dat een verschil maakt) die binnen die beperking waargenomen wordt. De beperking is de beperking van simultaneïteit die als de onvermijdelijke stappen in het proces waarneembaar is.

De intensiteit κ is dus het reëel getal dat de eigenwaarde is van de projectie van een van de elkaar uitsluitende toestanden op de andere. In het algemeen is een eigenwaarde een getal κ dat een transformatie T kan uitdrukken van een (eventueel vectoriële) variabele v zodanig dat T(v)=κv.

We zullen gedetailleerd onderzoeken wat het behoud van de verhouding κ betekent in de klassieke benadering van evenwicht als in de dynamische benadering van evolutie.

Gevolgen

Ervaren is onvermijdelijk en kan niet onderscheiden worden van iets-anders-te-laten-gebeuren. Iets gebeurt altijd in het grootst mogelijke universum dat aspecten heeft dat het ervarend agens (nog) niet kan hanteren om zijn werkelijkheid op te spannen en dat z(h)ij enkel kan aanvaarden als een onvermijdelijk spoor. Het ervarend agens evolueert onvermijdelijk van toestand naar toestand. Toestanden sluiten elkaar uit en zijn juist daardoor uitdrukking van de beperkingen (en mogelijkheden) van het agens in zijn context. Dit noemen we “veranderen”. Veranderen in het grootst mogelijke universum is onvermijdelijk. Snelheid als uitdrukking van de beperkingen is dus onvermijdelijk en de keuze van een referentie is volledig vrij en evenzeer onvermijdelijk. De eenheid van (proces)snelheid hebben we geconstrueerd als een gecollapste haakuitdrukking die een gewogen vorm is van een ervaren uitdrukking. Snelheid is onvermijdelijk en inherent aan het-ervaren-nu maar fundamenteler dan de toestand zelf die verandert in het grootst mogelijke universum omdat juist de onvermijdelijkheid-van-ervaren twee toestanden genereert die dan het begrip snelheid kunnen definiëren gegeven de context en het verschil van twee toestanden de éne telbare dimensie genereert die geen enkel absoluut standpunt veronderstelt omdat daarmee lokaal de nulvector kan gecreëerd worden en die we dus kunnen interpreteren als de waarnemingsresolutie.

Het agens-in-context zal altijd iets ervaren dat afwijkt van datgene dat stabiel blijft (en dat dus zijn waarnemingsresolutie bepaalt). De evolutie van toestand naar toestand kunnen we zowel als minimaal als maximaal beschouwen doordat er een verhouding ontstaat (waarvoor een invers kan gedefinieerd worden) van “het verschil met een referentietoestand in de ene ervaren toestand” met “het verschil met een referentietoestand in de andere ervaren toestand”, en dat dit voor elk paar toestanden geldt. Die evolutie is het gedrag dat waargenomen kan worden van een entiteit (eenheid) die niet verandert. Wat er waargenomen wordt, wordt beschreven door onderscheidingen die de entiteit niet karakteriseren, enkel zijn gedrag beschrijven en dit is context afhankelijk. Een wetenschappelijke beschrijving van dat gedrag vereist dat die context duidelijk in de meetprocedure beschreven wordt en dat enkel toevallige aspecten het gedrag meetbaar maken.

Merk op dat we niet méér moeten veronderstellen. Het begrip “toestand” is enkel misleidend wanneer men er (gewoonlijk intuïtief) van uitgaat dat een volledige beschrijving van de toestand mogelijk en noodzakelijk is voor alles wat het agens kan ervaren, terwijl hier alleen maar nodig is dat twee welgevormde haakuitdrukkingen elkaar uitsluiten om ze als toestand te kunnen benoemen (en dat is agens-in-context afhankelijk), van waaruit onvermijdelijk (dus in het grootst mogelijke universum) een snelheid volgt als verschil van een toestand met een referentie toestand. Die snelheid kan dan ook veranderen en aan die verandering kunnen we een intensiteit toekennen die ook nul kan zijn. Die intensiteit is die van een onvermijdelijke dus dynamische verandering. Een snelheid van verandering wordt ook een versnelling genoemd en dat is dus ook wat bedoeld wordt met het begrip “processnelheid” wat dan ook impliceert dat we geen versnelling (en wel snelheid) kunnen modelleren als een intensiteit die nul is.