Nemen we y als referentie punt dan kunnen we elk punt sommeren met y en vinden we als 1-splitsing:
Uitgaande van de modellering van onmogelijkheid (<<>>) en onvermijdelijkheid (<>) kunnen we op een eenvoudige wijze dynamiek modelleren in het haakformalisme zonder een nieuw axioma nodig te hebben. We zullen aantonen dat dynamiek het verschil is van de intensiteit van de waardetoekenning aan twee toestanden in het grootste universum. Een verschil maken impliceert een maximaal (of minimaal) verschil en zo is dynamiek gegrond in de onvermijdelijke erkenning dat toestanden (van een agens-in-context) elkaar uitsluiten en dat dit gemodelleerd wordt door een “waarnemingsresolutie”, een verschil dat een verschil maakt voor het agens-in-context.
Iets een waarde geven (dus iets ervaren) is onvermijdelijk. We beschouwen (elkaar uitsluitende) toestanden (onmogelijk simultaan te ervaren) die elkaar opvolgen x0, x1, x2,… en daardoor sporen genereren die strikt geordend zijn. Bij het onvermijdelijk ervaren van deze toestanden hebben de toestanden een ervaringswaarde. Die is waar te nemen als een intensiteit van een eenheid, minimaal een ja voor iets maar soms ook het getal van het simultaneïteitsinterval met infimum de waargenomen toestand <<>>⊕<xk>, dit is namelijk de uitdrukking voor een xk die niet verschillend is van <>. De toestanden kunnen gerelateerd zijn met (en gecorreleerd worden met) een voldoende blijvend spoor in een beschikbaar medium (onderscheidingen universum) dat de verandering waarneembaar maakt. De index markeert de verschillende “momenten in de tijd” (het zijn die toestanden die elkaar uitsluiten en geen andere, het begrip "tijd" en het begrip "proces" hebben enkel betekenis in die context) en markeert ook de elkaar uitsluitende sporen die waarneembaar zijn. Als toestanden elkaar uitsluiten is het onvermijdelijk dat er een laatst toegevoegde onderscheiding kan gevonden worden. We kunnen dit gebruiken in het creatief product. Als we steeds dezelfde onderscheiding gebruiken is het (niet commutatief) creatief product associatief en is een invers gedefinieerd. Dat is dus het geval voor de hier gebruikte laatst toegevoegde onderscheiding.
(x⊗x)ℵ=x, (y⊗y)ℵ=y, (x⊗y)ℵ=h, (y⊗x)ℵ=h-1, ...
Na het ervaren van een toestand (die dus een andere uitsluit) wordt onontkoombaar een andere toestand bereikt die van de eerste verschilt (anders zouden twee toestanden niet te onderscheiden zijn). Er is een niveau in een tralie te vinden dat als de invariante entiteit kan geïnterpreteerd worden die gerealiseerd wordt in elke beschouwde toestand. We zeggen dan dat de beschouwde toestanden xi varianten zijn (concrete realisaties) van die invariante entiteit die we “de toestand van de entiteit” noemen. De toestand van de entiteit is dus een abstractie die in verschillende concrete realisaties kan herkend worden, abstractie omdat deze toestand in een kleiner universum kan beschreven worden, een universum met minder onderscheidingen dan de onderscheidingen die nodig zouden zijn om een variant uniek te markeren (met een laatst toegevoegde onderscheiding). Aan de toestand van de entiteit kunnen we dus een intensiteit xi toekennen. In het meest eenvoudige geval is dat één getal, één spoor, maar dit is gemakkelijk uit te breiden naar meerdere getallen die aan één toestand gecorreleerd zijn wanneer meerdere getallen moeten gebruikt worden om het punt te beschrijven dat in een toestandsruimte ingenomen wordt in één bepaalde concreet gerealiseerde toestand.
We kunnen de verschillen berekenen van die intensiteiten. Dat betekent dat we twee verschillende momenten in de ordeningsparameter moeten veronderstellen, stel het moment gemarkeerd met 1 en het moment gemarkeerd met 0, dus we berekenen (de intensiteit van) x1-x0, en dan ook misschien x2-x0, …, xi-x0, .... Het verschil is hoe dan ook een relatief verschil van iets. Inderdaad: de verschillen zijn niet anders als van elke intensiteit een zelfde getal afgetrokken of opgeteld wordt, bijvoorbeeld x1-x0=(x1-g)-(x0-g). Met de expliciete vermelding van de eenheid e wordt dit dan (x1-x0)•e=(x1-g)•e-(x0-g)•e. Het is niet uit te sluiten dat g astronomisch groot of astronomisch klein zou zijn, dit maakt hoe dan ook geen verschil dat een verschil maakt.
Het verschil van toestanden genereert niet enkel een verschillende intensiteit maar ook een nieuwe eenheid. Is er geen verschil, dan is er geen toestand en in het ervaren van een toestand ervaart men altijd een verschil.
We bewijzen nu dat het verschil van een toestand x met een andere toestand y, dus (<x>⊕y), een noodzakelijke voorwaarde is voor de toestand x en dus x een voldoende voorwaarde is voor (<x>⊕y). We moeten dus bewijzen dat de disjunctie van (<x>⊕y) en <x> niet verschillend is van <>.
We drukken eerst uit dat x en y elkaar uitsluiten, dus de conjunctie <>⊕<x>⊕<y>⊕x•y=<<>> of dus <x>⊕<y>⊕x•y=<>
De disjunctie van (<x>⊕y) en <x> is <<>>⊕<(<x>⊕y)>⊕<<x>>⊕<(<x>⊕y)•<x>>
<<>>⊕x⊕<y>⊕x⊕<(<<>>⊕y•<x>)>
<<>>⊕<x>⊕<y>⊕<>⊕y•x
<x>⊕<y>⊕y•x
<>
Deze laatste stap hebben we hierboven bewezen door te veronderstellen dat zowel x als y toestanden zijn.
QED
Dit bewijs is formeel heel helder maar intuïtief moeilijk met woorden af te leiden. Bijvoorbeeld in de klassieke uitspraak “indien x dan (<x>⊕y)”. Terwijl duidelijk is dat “indien we een toestand ervaren er een toestand moet zijn die niet ervaren is en dus een toestand die enkel kan gebeuren en dus waarde <<>> heeft, en dan zal de som van <x> en y de waarde <> hebben.
Dynamiek kunnen we onderzoeken doordat het verschil van twee elkaar uitsluitende toestanden met een van de toestanden simultaan zal zijn.
Het verschil van toestanden is juist wat het begrip “dynamiek” uitdrukt en wordt dus rechtstreeks uit <<>> afgeleid en de som operatie zonder extra veronderstellingen. In het haakformalisme is dat dus helemaal geen mysterie.
Om de notaties eenvoudig te houden schrijven we de twee toestanden als x en y en zo één verschil als (<x>⊕y). We kunnen ons dan voorstellen dat een van beide een referentiefunctie vervult. Dat verschil is een origineel nieuwe onderscheiding, want noch met enkel toestand x (dus x0), noch met enkel toestand y (dus x1) is dat verschil beschikbaar, het is een relatie tussen toestanden en dus slechts beschikbaar als relatie tussen twee verschillende toestanden, als berekening vanuit twee verschillende toestanden, dus als berekening vanuit verschillende elkaar uitsluitende tijdstippen (als reconstructie gezien vanuit een later moment, of als anticipatie gezien vanuit een vroeger moment), berekening die uitgevoerd wordt met de intensiteiten van de eenheden x en y, eenheden die elkaar uitsluiten. De berekening geeft een waarde aan een nieuwe eenheid, namelijk (<x>⊕y).
We noteren y-x∼(<x>⊕y)=<y>•(<>⊕x•y) en we merken op dat x•y de afgeleide is naar ℵ van (x⊗y)ℵ. We kunnen hetzelfde doen voor de projectoren van de toestanden, we noteren het verschil van projectoren dus (<>⊕y)⊕<(<>⊕x)>=<>⊕y⊕<<>>⊕<x>=(<x>⊕y)=<y>•(<>⊕x•y) en uiteraard is dat geen andere relatie dan bij het verschil van toestanden. Een verschil van projectoren van toestanden onderscheidt zich niet van een verschil van toestanden. We merken ook op dat x•y telbaar is, dus dat het zin heeft een intensiteit aan de eenheid x•y te verbinden en deze dus te beschouwen als een entiteit. We merken ook op dat de operatie van het berekenen van een verschil een universele involutie is. We merken ook op dat het verschil van twee welgevormde haakuitdrukkingen die niet elkaars inbedding zijn onvermijdelijk een gecollapste haakuitdrukking genereert, die de interpretatie geeft dat er een gerelateerde welgevormde haakuitdrukking niet verschillend is van <>, en dus ervaren is, en ervaren is onvermijdelijk. Een gecollapste haakuitdrukking is altijd een ervaren haakuitdrukking die gewogen is met een welgevormde haakuitdrukking en kan dus de toestand die op dat moment ervaren is modelleren.
Het verschil (<x>⊕y), de gecollapste haakuitdrukking, laat altijd toe een simultaneïteitsinterval te construeren dat eveneens een gecollapste haakuitdrukking is. We construeren nu het simultaneïteitsinterval met de extrema x en (<x>⊕y) en beschouwen deze met de laatst toegevoegde onderscheiding ℵ, en we noemen dit interval A. Hierbij kunnen we y begrijpen als een referentie.
A=(x⊗(<x>⊕y))ℵ=(<y>•<x•y>⊗<y>•(<>⊕x•y))ℵ=<y>•(<x•y>⊗(<>⊕x•y))ℵ
Het creatief product van een toestand en een verschil van toestanden is dus van het type gewogen (<H>⊗(<>⊕H))ℵ met H de afgeleide naar ℵ van het creatief product van de twee betrokken toestanden x en y. We merken op dat de afgeleide naar ℵ van het type (<H>⊗(<>⊕H))ℵ niet anders is dan <H>•(<>⊕H) en dus (<>⊕H), een van de termen van het creatief product. De afgeleide x•y van (x⊗y)ℵ is onafhankelijk van ℵ en de tweede afgeleide naar ℵ heeft dus de waarde <<>> en het is onvermijdelijk dat deze eenheidswaarde een intensiteit heeft die we kunnen interpreteren als een scalair en scalairen zijn de kwantificeringen die moeten gebruikt worden in het stappenmodel. Aangezien x en y elkaar uitsluitende toestanden zijn, is er een universum te creëren waarin x•y een atoombuur is. Met behulp van enkel gewogen atoomburen is gelijk welke welgevormde haakuitdrukking te construeren. Een voorbeeld van weging is <<disjunctie niet verschillend van exclusieve disjunctie>> met een intensiteit.
We drukken A nu uit als een vectorsom. A=(x⊗(<x>⊕y))ℵ=<x>⊕<(<x>⊕y)>⊕<ℵ•x>⊕ℵ•(<x>⊕y)=<y>⊕ℵ•x⊕ℵ•y.
We bewijzen dat A ook in een vorm kan geschreven worden met toevoeging van een projector:
(x⊗<y>))(<>⊕<ℵ>)=<x>⊕y⊕(<>⊕<ℵ>)•<x>⊕(<>⊕<ℵ>)•<y>=<x>⊕y⊕x⊕ℵ•x⊕y⊕ℵ•y=<y>⊕ℵ•x⊕ℵ•y=A.
QED
De afgeleide naar (<>⊕<ℵ>) is <x•y>.
Als gevolg van de distributiviteit van som ten opzichte van het creatief product geldt ook dat A⊕y=(x⊕y⊗(<x>⊕<y>))ℵ=ℵ•x⊕ℵ•y. Hierbij zien we het patroon verschijnen van (P⊗<P>)ℵ=ℵ•P. Dit volgt ook uit A=(x⊗(<x>⊕y))ℵ voor een y=X. De afgeleide naar ℵ van A⊕y is (x⊕y)•(<x>⊕<y>) en dus <>⊕<x•y>⊕<x•y>⊕<>=(<<>>⊕x•y) en aangezien de afgeleide op een factor na bepaald is, is dit ook te schrijven als (<>⊕<x•y>).
A=<y>⊕ℵ•x⊕ℵ•y is een som van drie welgevormde haakuitdrukkingen en dit is dus ook niet verschillend van (<>⊕<y>)⊕(<>⊕ℵ•x)⊕(<>⊕ℵ•y), een som van drie projectoren. Zo'n simultaneïteitsinterval kan dus ook in drie vectoriële dimensies voorgesteld worden. We merken op dat A een gecollapste haakuitdrukking is en dus hebben we nu een constructie in drie vectoriële dimensies zoals we ook bewezen dat elke welgevormde haakuitdrukking in drie vectoriële dimensies voorgesteld kan worden. We kunnen (<<>>, ℵ) begrijpen als de coëfficiënten in de basis gemaakt door som en verschil van de extrema <x> en x⊕<y>, inderdaad <y>⊕ℵ•x⊕ℵ•y=<<>>•<y>⊕ℵ•(x⊕y)=<<>>•(<x>⊕(x⊕<y>)⊕ℵ•(x⊕y) maar de termen van A zijn ook de coëfficiënten in de basis van ℵ, inderdaad: de gecollapste haakuitdrukking <y>⊕ℵ•x⊕ℵ•y kunnen we ook schrijven als (y⊕<x>)•(<>⊕ℵ)⊕x•(<>⊕<ℵ>) in de basis van ℵ. Dus is het simultaneïteitsinterval (x⊗(y⊕<x>))ℵ de 1-de divergentie-splitsing (x, (y⊕<x>)).
De referentiefunctie die we voor y verondersteld hebben komt tot uitdrukking in het feit dat
A⊕y=<y>⊕ℵ•x⊕ℵ•y⊕y=ℵ•x⊕ℵ•y=ℵ•(x⊕y)
Het invers van A ten opzichte van ℵ is A-1=((<x>⊕y)⊗x)ℵ=<(<x>⊕y)>⊕<x>⊕ℵ•(<y>⊕x)⊕ℵ•x=<y>⊕<ℵ•x>⊕<ℵ•y> en is dus eveneens een som van drie projectoren. Dezelfde termen commuteren nu in de basis van ℵ, inderdaad: <y>⊕<ℵ•x>⊕<ℵ•y>=(<x>⊕y)•(<>⊕<ℵ>)⊕x•(<>⊕ℵ).
We kunnen dus ook de commutator A⊕<A-1>, die we noteren als [A, A-1], berekenen als <ℵ•x>⊕<ℵ•y> en zijn inbedding <A>⊕A-1 of dus [A-1, A] gelijk aan ℵ•x⊕ℵ•y. De constructie van een commutator scheidt op een éénduidige manier de laatst toegevoegde onderscheiding af, inderdaad [A, A-1]=<ℵ>•(x⊕y). Deze is niet anders dan de (inbedding van de) commutator van (x⊗<y>)ℵ. Inderdaad (x⊗<y>)ℵ=<x>⊕y⊕<ℵ•x>⊕<ℵ•y> en (<y>⊗x)ℵ=<x>⊕y⊕ℵ•x⊕ℵ•y en dus is het verschil van beide gelijk aan ℵ•x⊕ℵ•y. De commutator is dan ook gelijk aan A⊕y=A-1⊕y.
Aangezien x en y elkaar uitsluiten en dus <x>⊕<y>⊕x•y=<> is [A, A-1]=<ℵ•x>⊕<ℵ•y> ook niet anders dan ℵ•(<>⊕<x•y>). De ℵ in ℵ•(<>⊕<x•y>) geeft dus de intensiteit van een projector en die projector is een eenheid die in het universum opgespannen door x en y kan gevonden worden. Dus ℵ zullen we interpreteren als de intensiteit van de dynamiek met eenheid (<>⊕<x•y>).
We hebben het invers van A berekend ten opzichte van ℵ. A kunnen we echter ook met een projector als toegevoegde laatste onderscheiding voorstellen:
A=(x⊗<y>))(<>⊕<ℵ>)=<x>⊕y⊕(<>⊕<ℵ>)•<x>⊕(<>⊕<ℵ>)•<y>=<x>⊕y⊕x⊕ℵ•x⊕y⊕ℵ•y=<y>⊕ℵ•x⊕ℵ•y
Het invers van A ten opzichte van (<>⊕<ℵ>) is nu een andere uitdrukking:
(<y>⊗x))(<>⊕<ℵ>)=y⊕<x>⊕(<>⊕<ℵ>)•y⊕(<>⊕<ℵ>)•x=y⊕<x>⊕<y>⊕<ℵ•y>⊕<x>⊕<ℵ•x>=x⊕<ℵ•x>⊕<ℵ•y>.
Hiervoor moeten we dan een nieuw symbool kiezen, we kiezen voor A<>-1.
Dit leidt tot een andere commutator A⊕<A<>-1>, die we noteren als [A, A<>-1] en deze is <x>⊕<y>⊕<ℵ•x>⊕<ℵ•y>.
Dit de gecollapste haakuitdrukking (x⊕y)•(<>⊕ℵ), een uitdrukking in een deel van de basis van ℵ.
We construeren nu drie voorbeelden van A=(x⊗(<x>⊕y))ℵ=<y>⊕ℵ•x⊕ℵ•y.
Stel y=<<>> dan wordt A=(x⊗(<x>⊕<<>>))ℵ=<>⊕ℵ•x⊕ℵ en dus A⊕<<>>=ℵ•(x⊕<<>>)
Stel y=<> dan wordt A=(x⊗(<x>⊕<>))ℵ=<<>>⊕ℵ•x⊕<ℵ> en dus A⊕<>=ℵ•(x⊕<>)
Stel y=ℵ dan wordt A=(x⊗(<x>⊕ℵ))ℵ=<ℵ>⊕ℵ•x⊕ℵ•ℵ en dus A⊕<>=ℵ•(x⊕<>)
De laatste veronderstellingen zijn niet verschillend van elkaar.
We interpreteren dit als volgt: de laatst toegevoegde onderscheiding geeft in het ervaren zelf een intensiteit aan een projector die hier als eenheid functioneert.
Met dezelfde onderscheidingen kunnen we ook een ander interval construeren.
We construeren nu drie voorbeelden van B=(y⊗(<y>⊕x))ℵ=<x>⊕ℵ•y⊕ℵ•x.
Stel x=<<>> dan wordt B=(y⊗(<y>⊕<<>>))ℵ=<>⊕ℵ•y⊕ℵ en dus B⊕<<>>=ℵ•(y⊕<<>>)
Stel x=<> dan wordt B=(y⊗(<y>⊕<>))ℵ=<<>>⊕ℵ•y⊕<ℵ> en dus B⊕<>=ℵ•(y⊕<>)
Stel x=ℵ dan wordt B=(y⊗(<y>⊕ℵ))ℵ=<ℵ>⊕ℵ•y⊕ℵ•ℵ en dus B⊕<>=ℵ•(y⊕<>)
De laatste veronderstellingen zijn niet verschillend van elkaar.
Wat dit allemaal betekent wordt tastbaar met een voorbeeld in het drie onderscheidingen universum. Het drie onderscheidingen universum is voldoende omdat ℵ uiteindelijk het “grootste” universum bepaalt waarin x en y moeten uitgedrukt worden en we moeten het patroon niet ingewikkelder maken dan nodig. Stel x als 1100 en y als 0111, twee elkaar uitsluitende punten in het twee onderscheidingen universum die niet elkaars inbedding zijn (inderdaad, hun conjunctie is niet verschillend van 1111 en de inbedding van x is 0011 en dit is verschillend van 0111). Om zo algemeen mogelijk te blijven veronderstellen we ook niet dat ze punten zijn van hetzelfde niveau. Dus (<x>⊕y) is 0111⊕0011 en is dus 1x00.
We bewijzen nu op een alternatieve manier dat het verschil (<x>⊕y) een noodzakelijke voorwaarde is voor elke toestand x en dus x een voldoende voorwaarde is voor (<x>⊕y). Inderdaad: de conjunctie van x en (<x>⊕y) is de conjunctie van 1100 en 1x00 en dat is dus 1100 en dat is niet anders dan x, de disjunctie is 1x00 en dat is niet anders dan (<x>⊕y). Dus x en (<x>⊕y) zijn de extrema van het interval. Dat betekent dus dat (<x>⊕y) een noodzakelijke voorwaarde is voor x en dus x een voldoende voorwaarde is voor (<x>⊕y). QED.
We kiezen nu een punt uit een universum met één onderscheiding meer en genereren daarmee een interval en zijn invers in het hoogste universum. We geven daar twee voorbeelden van die dus aantonen dat hiermee het patroon ontstaat van een don’t care op een bepaalde positie en in een derde voorbeeld geven we ook aan dat we voor sommige keuzen geen punt in het hoogste universum bereiken, en wat daarvan de karakteristiek is.
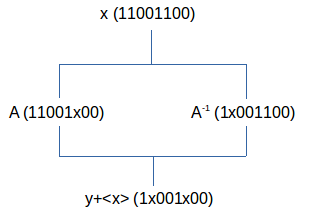
Stel ℵ als laatst toegevoegde onderscheiding voor als 11110000. Dus ℵ•x wordt uitgedrukt door 11000011 (en de bitstring van x moet daarvoor éénmaal herhaald worden). Dus ℵ•y wordt uitgedrukt door 01111000 (en de bitstring van y moet daarvoor éénmaal herhaald worden). Het interval A is dan 10001000⊕11000011⊕01111000=11001x00. Het interval A-1 is dan 10001000⊕00111100⊕10000111=1x001100.
Stel ℵ als laatst toegevoegde onderscheiding voor als 10010100. Dus ℵ•x wordt uitgedrukt door 10100111 (en de bitstring van x moet daarvoor éénmaal herhaald worden). Dus ℵ•y wordt uitgedrukt door 00011100 (en de bitstring van y moet daarvoor éénmaal herhaald worden). Het interval A is dan 10001000⊕10100111⊕00011100=1x001100. Het interval A-1 is dan 10001000⊕01011000⊕11100011=11001x00.
Stel ℵ als laatst toegevoegde onderscheiding voor als 11110111. Dus ℵ•x wordt uitgedrukt door 11000100 (en de bitstring van x moet daarvoor éénmaal herhaald worden). Dus ℵ•y wordt uitgedrukt door 01111111 (en de bitstring van y moet daarvoor éénmaal herhaald worden). Het interval A is dan 10001000⊕11000100⊕01111111=11001100. Het interval A-1 is dan 10001000⊕00111011⊕10000000=1x001x00. Beide intervallen zijn punten uit het twee onderscheidingen universum.
Wanneer we kiezen voor de laatst toegevoegde onderscheiding als 11110000, dan bekomen we steeds als intervallen een punt in het drie onderscheidingen universum.
Aangezien <<A><A-1>> niet anders is dan x en AA-1 niet anders is dan (<x>⊕y) ontstaat er dus een 1-splitsing, bijvoorbeeld:

Nemen
we y als referentie punt dan kunnen we elk punt sommeren met y en
vinden we als 1-splitsing:
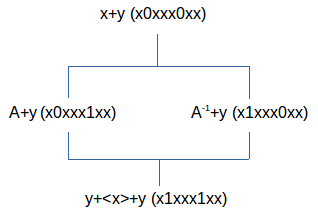
Als
we de conventie volgen om het extremum met enkel hoogbits bovenaan te
nemen dan schrijven we dat als:
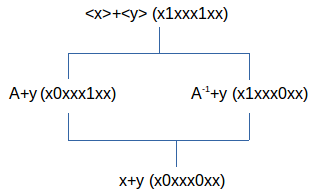
Deze
structuur is af te beelden op een één onderscheiding universum.
De beide extrema zijn symmetrische uitdrukkingen en dit betekent dat x en y hetzelfde patroon vertonen, uitwisselbaar zijn. Wanneer we stellen dat A=(x⊗(<x>⊕y))ℵ=<y>⊕ℵ•x⊕ℵ•y, dan kunnen we ook een B onderscheiden met B=(y⊗(<y>⊕x))ℵ=<x>⊕ℵ•x⊕ℵ•y en dus kunnen we een tweede structuur maken met <x>⊕<y>, B⊕x, B-1⊕x en x⊕y met exact dezelfde ℵ. Namelijk A⊕y=B⊕x=ℵ•x⊕ℵ•y. Dit is niet anders dan [A-1, A]. We kunnen ook berekenen dat A⊕B=<x>⊕<y>⊕<ℵ•x>⊕<ℵ•y> en dit is niet anders dan het tweede type commutator [A, A<>-1].
Dit betekent dat we exact hetzelfde patroon op twee manieren kunnen herkennen, een manier die we als A voorgesteld hebben en een manier die we als B voorstellen. Dit is uiteindelijk te herleiden tot een verschil van referentie: keuze van y leidt tot A, keuze van x leidt tot B. Het vectorproduct x•y kan voorstellen of beide referenties dezelfde waarde hebben of tegengestelde waarde.
We berekenen nu x•y: 01000100.
Dus x•y=<> is gegeven door 0x000x00. In dat geval hebben x en y tegengestelde waarde en dan is de commutator <ℵ•x>⊕<ℵ•y> gelijk aan nul.
We berekenen nu de commutator uit het eerste voorbeeld, dus 11001x00⊕0x110011=x1xxx0xx. Inderdaad, in de gecollapste tralie met die zes betekende bits is x1xxx0xx niet te onderscheiden van xxxxxxxx.
We berekenen nu de commutator uit het tweede voorbeeld, dus 1x001100⊕00110x11=x0xxx1xx. Inderdaad, in de gecollapste tralie met die zes betekende bits is x0xxx1xx niet te onderscheiden van xxxxxxxx.
We berekenen nu de commutator uit het derde voorbeeld, dus 11001100⊕0x110x11=x1xxx1xx. Inderdaad, in de gecollapste tralie met die zes betekende bits is x1xxx1xx niet te onderscheiden van xxxxxxxx.
In het andere extreem is x•y=<<>> gegeven door x1xxx1xx en we zien dus dat de twee uitersten voor de afgeleide een 1-splitsing uitvoeren. Dit is de 1-splitsing die overeenkomt met de orthogonale basis (<>⊕x•y) of 1x111x11 versus (<>⊕<x•y>) of x1xxx1xx. In het ene deel van de splitsing zijn er zes betekende bits, in het andere deel zijn er twee betekende bits. We zien dus onmiddellijk dat, als ℵ in een groter universum moet uitgedrukt worden, dat de 1-splitsing waarin we y als referentie in de som gebruikt hebben niet verschilt van de volgende 1-splitsing.
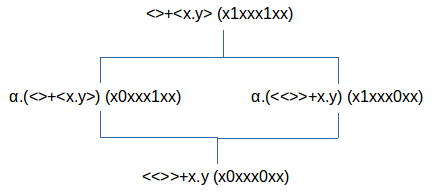
Deze
structuur maakt duidelijk dat de 1-splitsing uitsluitend tot de
dualiteit van ℵ versus <ℵ> te reduceren is, maar dat
dynamiek op twee manieren zal kunnen voorgesteld worden, een manier
met referentiekeuze x en een manier met referentiekeuze y.
Deze structuur is de structuur van een gecollapste atoombuur.
Aangezien ℵ per definitie het grootste universum codeert waarin de welgevormde haakuitdrukkingen x en y moeten uitgedrukt worden is het, in dit geval, het verschil tussen twee en drie onderscheidingen. Dit verschil is 1 en dus 21 geeft het aantal waarmee het bit patroon in het universum van x•y moet vermenigvuldigd worden, inderdaad we hebben het patroon van x•y moeten verdubbelen om ook in het universum van ℵ te kunnen functioneren. Noteer dat de uitdrukking x•y ook in staat is een x en y te combineren die eventueel in een verschillend universum hun meest eenvoudig bitstring patroon kunnen hebben. Stel dat ℵ een vier onderscheidingen universum zou binnengebracht hebben dan zouden we als factor van vermenigvuldiging 22 of 4 gevonden hebben enz... Dit maakt duidelijk dat het verschil kwantitatief uit te drukken is: de afgeleide naar ℵ heeft de intensiteit van het grootste universum dat in een 1-splitsing kan opgesplitst worden. De opsplitsing wordt bepaald door x•y, en, indien we dat willen als een volgende stap in de abstractie, dan is het patroon (onafhankelijk van de eenheid die de projector (<>⊕<x•y>) is) te kwantificeren door een aantal bits. Bijvoorbeeld het inwendig product van het verschil van x en y (dus het aantal verschillende bits, in dit geval 1) of de verhouding die het aantal gelijke ten opzichte van verschillende bits geeft voor x en y (in dit geval dus 1 gelijk en 3 verschillend, dus een verhouding van 1/3). Dus ℵ codeert de factor (de intensiteit van de eenheid 1) waarmee deze verhouding vermenigvuldigd wordt, voor een grootste universum dat slechts 1 onderscheiding meer heeft is dit 21(1/3), voor 2 extra onderscheidingen is dit 22(1/3), …, voor het grootste universum dat n onderscheidingen meer heeft is dit 2n(1/3). Een ander voorbeeld zou de inwendige discriminatie kunnen zijn. Het enige wat we doen is verschillende eenheden gebruiken, ze hebben allemaal dezelfde intensiteit.
We interpreteren de commutator niet verschillend van nul, of dus x=<y>, of dus <>⊕x•y=<<>>, nu als volgt: een model waarin de relaties associatief en commutatief zijn (de commutator is nul) is enkel mogelijk wanneer een projectieve eenheid, in dit geval dus (<>⊕x•y), niet verschillend van <<>> verondersteld wordt. In dat geval is er geen echt interval dat door een verschil van toestanden geconstrueerd wordt aangezien A=(x⊗(<x>⊕y))ℵ=<y>=x, dus “de extrema vallen samen”. Er is dus geen dynamiek. We kunnen A dan noteren als A=(x⊗<y>)ℵ=A=(<y>⊗x)ℵ=A=(x⊗x)ℵ=A=(<y>⊗<y>)ℵ en dit zijn welgevormde haakuitdrukkingen, geen projectoren dus enkel potentiële punten en geen ervaren punten. Dat betekent dus dat een model waarin de relaties associatief en commutatief zijn geen verandering modelleert, wat nu als volgt kan geïnterpreteerd worden: de “intensiteit van verandering” is niet waar te nemen, de projector <>⊕x•y heeft waarde <<>> en de intensiteit ervan verandert niet, de laatst toegevoegde onderscheiding speelt geen rol, het aantal onderscheidingen in het opgespannen universum verandert niet, er gaan geen onderscheidingen weg, er komen er geen bij, de laatst toegevoegde onderscheiding wordt niet ingebouwd. Die bepaalde “indien... dan...” constructie is immuun voor verandering, het is een stabiel deel van het groter geheel dat onvermijdelijk verandert maar nu niet gemodelleerd wordt, het is het deel dat invariant is voor de operatie van toevoeging van een onderscheiding (en dus ook een laatst toegevoegde ℵ) wat goed uitgedrukt wordt door de gelijkheid A=(x⊗x)ℵ=x. Er kan dan een symmetrie ten opzichte van de onvermijdelijke verandering waargenomen worden en dus een invariant.