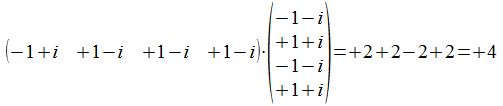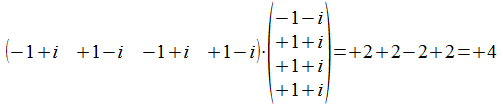Het inwendig product is een getal dat we kunnen construeren op basis van een 1-splitsing. We lijsten nu een aantal eigenschappen van dit getal waaruit blijkt hoe het gerelateerd is met aantallen en niveaus in een tralie.

Het inwendig product is een reëel getal

Per definitie kunnen met deze procedure enkel reële getallen ontstaan.

Het inwendig product is commutatief

Commutativiteit is onmiddellijk duidelijk vanuit de opbouw ervan. We nemen als voorbeeld een 1-splitsing op een vector met vier componenten die we als afbeelding nemen van welgevormde haakuitdrukkingen uit het twee-onderscheidingen universum. Het inwendig product van <<a><b>> en a is 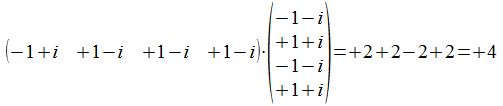en het inwendig product van a en <<a><b>> is .

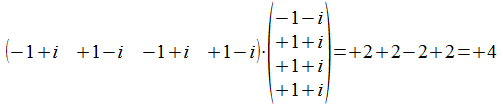Dit levert hetzelfde reëel getal op. In de Dirac notatie is dit dus <<<a><b>>|a>=<a|<<a><b>>> of ook <1110|1010>=<1010|1110>

Het inwendig product is lineair in de ket

Te bewijzen: <x|y+αz> = <x|y>+α<x|z>

Als willekeurig voorbeeld nemen we x als (-1-i +1+i -1-i +1+i)^T, y als (-1-i -1-i +1+i -1-i)^T en z als (+1+i +1+i +1+i -1-i)^T en dus is y+αz de kolomvector . <x|y+αz> is 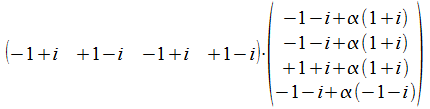en dit is de volgende som

(-1+i)(-1-i+α(1+i))+(1-i)(-1-i+α(1+i))+(-1+i)(1+i+α(1+i))+(1-i)(-1-i+α(-1-i)). Door de distributiviteit van de vermenigvuldiging is dit uiteraard gelijk aan de som van de volgende inwendig product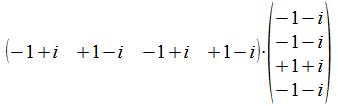en en 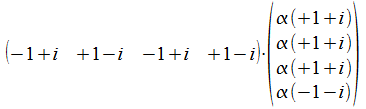en dit is uiteraard <x|y>+α<x|z>.

QED

Het inwendig product is anti-lineair in de bra

Te bewijzen: <αx+βy|z> = α*<x|z>+β*<y|z>

Als willekeurig voorbeeld nemen we x als (-1-i +1+i -1-i +1+i)^T, y als (+1+i -1-i +1+i +1+i)^T en z als (+1+i -1-i -1-i -1-i)^T en dus

α<x|+β<y| = {α(-1-i)+β(1+i), α(1+i)+β(-1-i), α(-1-i)+β(1+i), α(1+i)+β(1+i)}^T of {(α_r+α_ii)(-1-i)+(β_r+β_ii)(1+i), (α_r+α_ii)(1+i)+(β_r+β_ii)(-1-i), (α_r+α_ii)(-1-i)+(β_r+β_ii)(1+i), (α_r+α_ii)(1+i)+(β_r+β_ii)(1+i)}^T

Het is voldoende dat we de transpose van de eerste component onderzoeken, de berekening voor de volgende componenten verloopt analoog.

(α_r+α_ii)(-1-i) + (β_r+β_ii)(1+i)

We herschikken

(-α_r+α_i) - (α_r+α_i)i + (β_r-β_i) + (β_r+β_i)i

Van deze laatste uitdrukking is de transpose

(-α_r+α_i) + (α_r+α_i)i + (β_r-β_i) - (β_r+β_i)i

Deze term wordt nu vermenigvuldigd met -1-i, afkomstig van z

(-α_r+α_i)(-1-i) + (α_r+α_i)i(-1-i) + (β_r-β_i)(-1-i) - (β_r+β_i)i(-1-i)

(-α_r+α_i)(-1-i) + (α_r+α_i)(1-i) + (β_r-β_i)(-1-i) - (β_r+β_i)(1-i)

(α_r-α_i)+(α_r-α_i)i + (α_r+α_i)-(α_r+α_i)i - (β_r-β_i)-(β_r-β_i)i - (β_r+β_i)+(β_r+β_i)i

2α_r-2α_ii-2β_r+2β_ii

Dit kunnen we ook schrijven als

(α_r-α_ii)(-1+i)(-1-i) + (β_r-β_ii)(1-i)(-1-i)

En dit is de eerste component van

α*<x|z>+β*<y|z>

QED

Met het inwendig product normeren we vectoren naar een bepaald onderscheidingen universum

Voor een genormeerd n onderscheidingen universum geldt dat de vectoren met 2^-(1/2)(n+1) vermenigvuldigd moeten worden om een inwendig product van een punt met zichzelf gelijk aan 1 te bekomen.

Voorbeeld <1100|1100> is het inwendig product van 1100 met zichzelf

Als we nu elke component van de vectoren vermenigvuldigen met de getalfactor 2^-3/2 dan is het resultaat 1, waarmee we dus de normalisatie doorgevoerd hebben die specifiek is voor alle punten uit het twee onderscheidingen universum.

Dus na normering:

• Het inwendig product van een punt met zichzelf is 1

• Het inwendig product tussen punten die elkaars inbedding zijn is negatief en gelijk aan -1

Het inwendig product geeft een maat voor het verschil tussen de aantallen gelijke bits en verschillende bits

Nemen we nu eens twee willekeurige punten 00011100 (A) en 00001001 (B) en laten we onderzoeken hoe het inwendig product van beide opgebouwd wordt.

(-1+i, -1+i, +1-i, +1-i, +1-i, -1+i, -1+i, -1+i)•(+1+i, -1-i, -1-i, +1+i, -1-i, -1-i, -1-i, -1-i,)^T= -2+2-2+2-2+2+2+2=+4

Samengevat:

Het inwendig product is gelijk aan 2x het verschil tussen het aantal gelijke bits en het aantal verschillende bits.

Het gevolg hiervan is dat het inwendig product gelijk kan zijn aan nul. We kunnen op die manier een orthogonaliteit definiëren die ook geldt voor welgevormde haakuitdrukkingen. Deze orthogonaliteit is gerelateerd met het vectorproduct van de twee welgevormde haakuitdrukkingen: als het vectorproduct zich op centraal niveau bevindt dan zijn er evenveel hoogbits als laagbits en is het inwendig product dus nul. Voor twee welgevormde haakuitdrukkingen is het vectorproduct een unieke derde welgevormde haakuitdrukking.

Het inwendig product van een som (en verschil)

Het inwendig product van een som van 2 vectoren geeft 2x het aantal gelijke bits.

Voorbeeld: (-1-i, -1-i, 1+i, 1+i, 1+i, -1-i, -1-i, -1-i)^T+(1+i, -1-i, -1-i, 1+i, -1-i, -1-i, -1-i, -1-i)^T=(0, -2-2i, 0, 2+2i, 0, -2-2i, -2-2i, -2-2i)^T. En: (0, -2+2i, 0, 2-2i, 0, -2+2i, -2+2i, -2+2i)•(0, -2-2i, 0, 2+2i, 0, -2-2i, -2-2i, -2-2i)^T=+5(+8)

Het inwendig product van een verschil van vectoren geeft 2x het aantal verschillende bits.

Voorbeeld: (-1-i, -1-i, 1+i, 1+i, 1+i, -1-i, -1-i, -1-i)^T _– (1+i, -1-i, -1-i, 1+i, -1-i, -1-i, -1-i, -1-i)^T=(-2-2i, 0, +2+2i, 0, +2+2i, 0, 0, 0)^T. En: (-2+2i, 0, +2-2i, 0, +2-2i, 0, 0, 0)•(-2-2i, 0, +2+2i, 0, +2+2i, 0, 0, 0)^T=+3(+8)

Voor een n onderscheidingen universum geldt in het algemeen dat de vectoren met 2^-(1/2)(n+1) vermenigvuldigd moeten worden om een genormeerd universum te bekomen. Voor een 3 onderscheidingen universum geldt dus dat de vectoren met 2^-2 vermenigvuldigd moeten worden, dus de som (of verschil) van twee vectoren heeft een coëfficiënt 2^-1 en het inwendig product krijgt dus de factor 2^-2.

Het inwendig product is een metrische maat

We hebben aangetoond dat het niveauverschil tussen twee punten in de tralie van een bepaald universum aan de basis ligt van een metriek. Het aantal verschillende bits van p en q, m(p, q), hebben we gedefinieerd als de afstand tussen p en q. Het inwendig product van het verschil van beide vectoren geeft juist het dubbel van dit aantal verschillende bits.

Inwendig product als coëfficiënt van atomaire basisvectoren

<e₁|a> is het inwendig product van de meest linkse atomaire basisvector in het twee onderscheidingen universum met a en leidt tot 2: (-1+i, 0, 0, 0)•(-1-i, +1+i, -1-i, +1+i)^T. <e*₁|a> is dan het inwendig product van de reciproque van de meest linkse basisvector met a en leidt tot –2: (+1-i, 0, 0, 0)•(-1-i, +1+i, -1-i, +1+i)^T. Dit maakt duidelijk dat we haakvectoren kunnen beschouwen als een lineaire combinatie van basisvectoren waarbij de inwendig producten in de coëfficiënten optreden.

Voorbeeld

<<a><b>> stelden we voor als 1110 als bitvoorstelling en vertalen we nu in de vector (-1-i, 1+i, 1+i, 1+i)^T die de volgende som is van de basisvectoren (-1-i, 0, 0, 0)^T + (0,1+i, 0, 0)^T + (0, 0, 1+i, 0)^T + (0, 0, 0, 1+i)^T. We merken op dat we maar 4 van de 8 mogelijke basisvectoren gebruiken.

We berekenen nu de inwendig producten met alle 8 de basisvectoren om te onderzoeken welke eigenschappen de vier gebruikte gemeenschappelijk hebben:

(-1+i, +1-i, +1-i, +1-i)•(-1-i, 0, 0, 0)^T= +2

(-1+i, +1-i, +1-i, +1-i)•(0, -1-i, 0, 0)^T= -2

(-1+i, +1-i, +1-i, +1-i)•(0, 0,-1-i, 0)^T= -2

(-1+i, +1-i, +1-i, +1-i)•(0, 0, 0,-1-i)^T= -2

(-1+i, +1-i, +1-i, +1-i)•(+1+i, 0, 0, 0)^T= -2

(-1+i, +1-i, +1-i, +1-i)•(0, +1+i, 0, 0)^T= +2

(-1+i, +1-i, +1-i, +1-i)•(0, 0, +1+i, 0)^T= +2

(-1+i, +1-i, +1-i, +1-i)•(0, 0, 0, +1+i)^T= +2

Hieruit kunnen we besluiten dat een lineaire combinatie met alle (maar dus lineair afhankelijke) basisvectoren enkel de positieve inwendig producten gebruikt. Dit is de reden waarom men een inwendig product enkel als positief definiet definieert.

Als we de vectoren vermenigvuldigen met 2^-3/2 dan zijn de resultaten 2^-1/2

We kunnen nu ook noteren dat een willekeurig punt in het 1-splitsing universum kan geschreven worden als:

|a> = Σ α_ei|e_i> met som over de gebruikte basisvectoren (de 2ⁿ basisvectoren met n het aantal onderscheidingen) met α_ei = 2^-1<e_i|a>