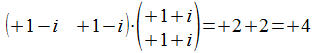
De constructie van het inwendig product en van het uitwendig product maakt het mogelijk universa te normaliseren. Dit is het eenvoudigst aan te tonen met een aantal voorbeelden.

Het een-onderscheiding universum

De vector <<>> wordt in het een-onderscheiding universum voorgesteld door (+1+i +1+i)^T, dus het inwendig product met zichzelf is

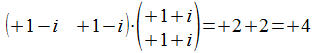
Met de normalisatiefactor 2^-1 wordt het inwendig product van <<>> (en <>) gelijk aan 1.

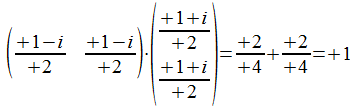
Met deze normalisatie factor wordt de operator die overeenkomt met <<>> (en <>) dan: 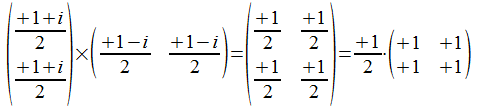en het spoor (de som van de diagonaalelementen) van de operator is 1.

De enige onderscheiding (en zijn inbedding) komt dan overeen met:

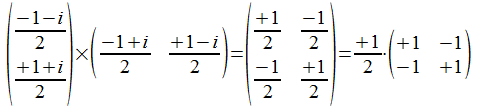
De operator zonder zijn normalisatie coëfficiënt zullen we de grondvorm van de operator noemen.

Het twee-onderscheidingen universum

De vector <<>> wordt in het twee-onderscheiding universum voorgesteld door (+1+i +1+i +1+i +1+i)^T, dus het inwendig product met zichzelf is

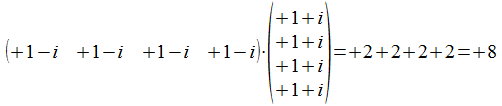
Met de normalisatiefactor 2^-3/2 wordt het inwendig product van <<>> (en <>) gelijk aan 1, en de operator die met <<>> overeenkomt is een 4x4 matrix met +1/4 in alle cellen en het spoor van de operator is 1.

Meer-onderscheidingen universa

Inductief is het is nu duidelijk dat de normalisatie factor voor de vectoren van een n onderscheidingen universum zal gegeven worden door 2^-(n+1)/2 . Er ontstaat dus een verschil tussen universa met even aantal onderscheidingen en oneven aantal onderscheidingen.

De vectoren van onderscheidingen universa met oneven aantal onderscheidingen zijn in modulo 3 voor te stellen, de vectoren van universa met een even aantal onderscheidingen niet. Maar dat is juist het voordeel, want we merken op dat er iets gewijzigd is aan de vertaling van de vector zelf in modulo3 formaat, immers: de factor 2^-oneven zal het teken van de vector wijzigen, de factor 2^-even kan dit niet doen aangezien die vertaling niet gedefinieerd is.

Bijvoorbeeld: als we de vector voor <<>> in een een-onderscheiding universum voorzien van de normalisatie voor dat universum (namelijk: 2^-1 en dit is een factor zonder breuk in de exponent), zie hoger, dan wordt elke cel van de operator ingenomen door het getal 2^-1, dat in modulo3 vorm overeenkomt met -1. Maar dat betekent dat in modulo3 vorm als operator staat (merk op dat dit nu een modulo3 berekening is, wat we aangeven met ∼): 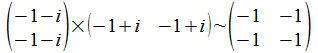en we merken op dat ook de vector van teken gewisseld is: de hoog-bit + wordt nu door de getalbit -1-i voorgesteld (en de laag-bit - wordt door de getalbit +1+i voorgesteld), in tegenstelling met de situatie waarin geen modulo3 omzetting gebeurt (namelijk .

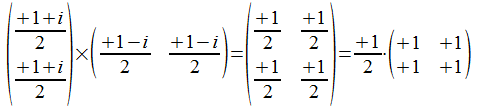Doen we nu hetzelfde in een twee-onderscheidingen universum dan gebeurt de normalisatie met een factor 2^-3/2, en wordt elke cel van de operator ingenomen door het getal 2^-2, waarvan de modulo3 waarde +1 is, en is er dus geen tekenwisseling.

Het werken met normalisaties met een reciproque macht van 2 zal dus zowel voor even als oneven universa leiden tot operatoren en vectoren met dezelfde signatuur. De voorstelling van de punten in dubbelbit strings zal dan onveranderd kunnen weergegeven worden, of ze zich nu in een even of oneven universum bevinden. Een reciproque macht van 2 blijkt daarmee de structuureenheid te zijn in deze operator constructie waarbij de cellen van de operatoren telbare getallen zijn.

Gecollapste universa

Een gecollapst universum heeft op minstens 1 positie in de bitstring een don't. Aangezien de normalisatiefactor enkel op betekende bits zijn invloed zal uitoefenen zullen we dus ook normalisaties kennen die verschillend zijn van reciproque machten van 2.