We hebben het
isomorfisme aangetoond van modulo 3 haakvectoren in bitstring
formaat met bitstrings met complexe getalcomponenten ±1±i.
Deze bitstrings kunnen nu op een nieuwe manier met elkaar
interageren, interactie die we op een fundamentele manier onderzocht
hebben met behulp van de operatoren
ε, υ, ν, νυ.
We zullen nu twee nieuwe operatoren construeren die we kunnen
inzetten om de structuur van een tralie op een nieuwe manier te
karakteriseren. De constructie gebeurt weer met behulp van een
product. We onderscheiden twee producten: het inwendig product en het
uitwendig product.
Het inwendig product
Het inwendig product wordt geconstrueerd door de geconjugeerde
transpose van een kolomvector met behulp van een gewone matrix
vermenigvuldiging te vermenigvuldigen met een tweede kolomvector.
Conjugatie wordt hier gebruikt in zijn interpretatie als operatie op
een complexe getalcomponent van een bitstring. Conjugatie is een
inwendige
involutie. De matrix vermenigvuldiging is goed gedefinieerd
aangezien de bewerking bestaat uit een vectorproduct en een vectorsom
die beide goed gedefinieerd zijn.
Voorbeelden:
De vector <<>> wordt in het 1-splitsing universum
als afbeelding van zijn bitstring voorstelling in het een
onderscheiding universum voorgesteld door (+1+i +1+i)T,
dus het inwendig product met zichzelf is
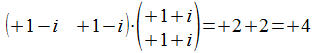 .
Het is hierdoor duidelijk dat ook het inwendig product van de vector
<> met zichzelf in het 1-splitsing universum als afbeelding
van zijn bitstring voorstelling in het een onderscheiding universum
gelijk aan +4.
.
Het is hierdoor duidelijk dat ook het inwendig product van de vector
<> met zichzelf in het 1-splitsing universum als afbeelding
van zijn bitstring voorstelling in het een onderscheiding universum
gelijk aan +4.
De vector a wordt in het 1-splitsing universum als afbeelding
van zijn bitstring voorstelling in het een onderscheiding universum
voorgesteld door (-1-i +1+i)T, dus het inwendig product
met <<>> is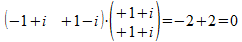
Merk op dat we in deze voorstelling van het haakformalisme
effectief getallen manipuleren en dat door deze constructie duidelijk
is dat een getal hier als operator gedefinieerd wordt. Deze definitie
resulteert enkel in reële getallen als operatoren. Het is met
deze reële getallen dat we eigenschappen van onderscheidingen
tralies zullen kunnen modelleren.
Het uitwendig product
Het uitwendig product wordt geconstrueerd door een kolomvector met
een Kronecker vermenigvuldiging te vermenigvuldigen met de
geconjugeerde transpose van een tweede kolomvector.
Voorbeelden:
De vector <<>> wordt in het 1-splitsing universum
als afbeelding van zijn bitstring voorstelling in het een
onderscheiding universum voorgesteld door (+1+i +1+i)T,
dus het uitwendig product met zichzelf is
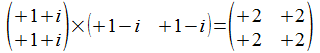 .
Met het uitwendig product ontstaan dus vanuit de vectoren met n
elementen n x n matrices of operatoren. De n-de rij van de matrix
wordt gevormd door de n-de component van de vector te
vermenigvuldigen met elke component van de geconjugeerde transpose
vector. De elementen van de operator kunnen per constructie enkel
reële getallen zijn.
.
Met het uitwendig product ontstaan dus vanuit de vectoren met n
elementen n x n matrices of operatoren. De n-de rij van de matrix
wordt gevormd door de n-de component van de vector te
vermenigvuldigen met elke component van de geconjugeerde transpose
vector. De elementen van de operator kunnen per constructie enkel
reële getallen zijn.
De vector <> wordt in het 1-splitsing universum als
afbeelding van zijn bitstring voorstelling in het een onderscheiding
universum voorgesteld door (-1-i -1-i)T, dus het
uitwendig product met zichzelf is
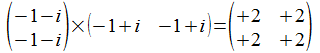 en
dit is exact dezelfde operator.
en
dit is exact dezelfde operator.
De vector a wordt in het 1-splitsing universum als afbeelding
van zijn bitstring voorstelling in het een onderscheiding universum
voorgesteld door (-1-i +1+i)T, dus het uitwendig product
met zichzelf is
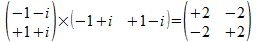
De vector <a> wordt in het 1-splitsing universum als
afbeelding van zijn bitstring voorstelling in het een onderscheiding
universum voorgesteld door (+1+i -1-i)T, dus het
uitwendig product met zichzelf is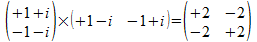 en
dit is exact dezelfde operator.
en
dit is exact dezelfde operator.
Het uitwendig product in het 1-splitsing universum als
afbeeldingen van bitstrings in het een onderscheiding universum van
a met <<>> is
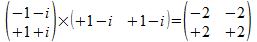 en
van <<>> met a is
en
van <<>> met a is
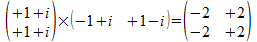
Besluit en overzicht van de mogelijkheden met de
nieuwe operaties
In het isomorfisme dat we geconstrueerd hebben van het
haakformalisme met complexe getallen als componenten van de bitstring
hebben we twee nieuwe operaties gedefinieerd: het inwendig product en
het uitwendig product. Beide leiden ze tot een resultaat dat
onafhankelijk is van de uitwendige
involutie (die de operatie van inbedding van een totale
haakvector is). Dit opent een belangrijk aantal nieuwe mogelijkheden
die we zeer goed kunnen gebruiken om de
relatie van relevantie verder te onderzoeken.
Deze afbeelding maakt het mogelijk om in één
formele voorstelling, de nieuw geconstrueerde operator voorstelling,
een potentieel punt voor te stellen onafhankelijk van zijn
inbedding. We zullen onderzoeken wat dit betekent wanneer we het
ervaren van een punt als het gebeuren van de inbedding van het punt
willen modelleren. Het is juist de unificatie van die beide
voorstellingen van een potentieel punt die ook gerealiseerd wordt
door de relatie
van relevantie. Dit betekent dat het gebruik van deze soort
matrix operatoren de formele voorstelling sterk vereenvoudigt maar
ook beperkt. Maar dit betekent ook dat deze nieuwe operatie de
mogelijkheid geeft om bestaande toepassingen
van matrix operatoren met reële componenten in het
haakformalisme te modelleren.
Het inwendig product genereert getallen die
verschillend zijn van +1 of -1. Dit geeft de mogelijkheid om een
verdere vereenvoudiging door te voeren door normalisatie:
we kunnen deze isomorfe afbeelding van het haakformalisme
normaliseren, waarbij het verschil tussen universa opgespannen door
een even aantal en een oneven aantal onderscheidingen verdwijnt. Met
andere woorden: dit soort isomorfisme geeft ons de mogelijkheid om
berekeningen uit te voeren op waarnemingen zonder dat we weten of
het relevante universum nu door een even aantal of oneven aantal
onderscheidingen opgespannen wordt en dit is dus een belangrijk
instrument om ook die a priori te verlaten. De normalisatie
herkennen we ook bij de toepassingen van waarschijnlijkheden.
Aangezien er bij de nieuwe operaties bewerkingen met de echte
getallen 1 en i uitgevoerd worden, moet er van universum tot
universum een andere normalisatiefactor
toegepast worden om de structuurinformatie (te wijten aan de
operatoren) te kunnen scheiden van de informatie die te wijten is
aan de telbaarheid
van entiteiten. Dit zijn dan normalisatiefactoren met breuken in
de exponent zodanig dat de overeenkomst met de modulo3 werkwijze
omzeild wordt en ook het verschil even/oneven universum verdwijnt.
Inderdaad tonen
we aan dat in het algemeen de coëfficiënt waarmee een
vector in het operatorformalisme genormeerd wordt 2-(n+1)/2 is,
met n het aantal onderscheidingen. Met een voorbeeld: is het aantal
onderscheidingen 2 in de voorstelling van a, dan moet de coëfficiënt
2-3/2 zijn om voor <> en <<>> altijd
een matrix te vinden waarvan het spoor gelijk is aan 1. Merk op dat
de exponent van 2 een breukvorm heeft (die dus niet in modulo3
uitgedrukt kan worden). Om de invloed daarvan te begrijpen moeten we
de normalisatie in het nieuw operator formalisme begrijpen en
aantonen hoe dit exact overeenkomt met een modulo3 benadering.
De nieuwe uitwendig product operatoren worden geconstrueerd
met behulp van het Kronecker product van de vector en zijn
toegevoegde, waarbij het getal i met zijn normale karakteristiek van
(-1)1/2 in de vector (en alleen maar in de vector en niet
in operatoren) functioneert. Met het Kronecker product van de
operatoren van een universum bereikt men ook enkel (!) de helft van
de operatoren van een hoger universum, namelijk de operatoren die
overeenkomen met het centraal niveau (en de extrema) in dat hoger
universum.
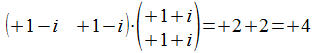 .
Het is hierdoor duidelijk dat ook het inwendig product van de vector
<> met zichzelf in het 1-splitsing universum als afbeelding
van zijn bitstring voorstelling in het een onderscheiding universum
gelijk aan +4.
.
Het is hierdoor duidelijk dat ook het inwendig product van de vector
<> met zichzelf in het 1-splitsing universum als afbeelding
van zijn bitstring voorstelling in het een onderscheiding universum
gelijk aan +4.![]()
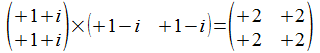 .
Met het uitwendig product ontstaan dus vanuit de vectoren met n
elementen n x n matrices of operatoren. De n-de rij van de matrix
wordt gevormd door de n-de component van de vector te
vermenigvuldigen met elke component van de geconjugeerde transpose
vector. De elementen van de operator kunnen per constructie enkel
reële getallen zijn.
.
Met het uitwendig product ontstaan dus vanuit de vectoren met n
elementen n x n matrices of operatoren. De n-de rij van de matrix
wordt gevormd door de n-de component van de vector te
vermenigvuldigen met elke component van de geconjugeerde transpose
vector. De elementen van de operator kunnen per constructie enkel
reële getallen zijn.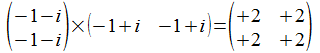 en
dit is exact dezelfde operator.
en
dit is exact dezelfde operator.