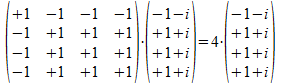
De projectie van een vector op zichzelf, dus door gebruik te maken van de projector die overeenkomt met de vector is de vector zelf. Laten we <<a><b>> eens projecteren op P<<a><b>> in de grondvorm:
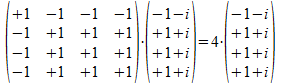
Houden we nu rekening met 2-3/2 die de factor is die we aan de vectoren toegekend hebben in een 2-onderscheidingen universum dan is het resultaat de vector <<a><b>> met de factor 2-3/2. Dus een operator zal de vector |x> waarvan hij het uitwendig product |x><x| is, afbeelden (op projecteren) op de vector zelf met als factor 1, exact het gedrag dat we van een projector verwachten.
Houden we geen rekening met de factoren die de vectoren normaliseren, en houden we enkel rekening met de grondvormen, dan vinden we als factor van het resultaat het aantal bits dat gelijk is (twee dezelfde vectoren in een 2-onderscheidingen universum hebben 4 gelijke bits) min het aantal dat verschillend is (in dit geval dus nul).
De projectoren projecteren een willekeurig punt op de vector die de projector geconstrueerd heeft.
Laten we <<a><b>> eens projecteren op P<<>>
in de grondvorm:
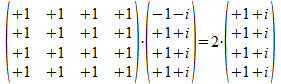
Laten we b eens projecteren op P<<a><b>>
in de grondvorm:
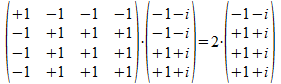
In beide gevallen is het rechterlid de vector die de projector van het linker lid geconstrueerd heeft. We hebben geen rekening gehouden met de factoren die de vectoren normaliseren en we vinden als factor van het resultaat het aantal bits dat gelijk is min het aantal dat verschillend is.
Het is duidelijk dat bijvoorbeeld het laatste voorbeeld ook als
volgt kan geschreven worden omdat (+1+i) een getal is:
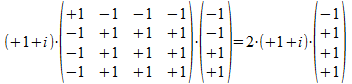
We merken nu op dat (1+i) een complex getal is dat verschillend is van nul, dus we kunnen de linker term en de rechter term delen door (1+i) en dus geldt:
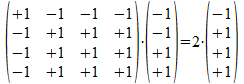 en beide vectoren zijn nu bitstrings met reële getallen en de
hint naar de constructie van de projector is dus ook verdwenen. Exact
datzelfde zouden we ook bereikt hebben met het perplex getal (1+j) en
uiteraard ook met een reëel getal.
en beide vectoren zijn nu bitstrings met reële getallen en de
hint naar de constructie van de projector is dus ook verdwenen. Exact
datzelfde zouden we ook bereikt hebben met het perplex getal (1+j) en
uiteraard ook met een reëel getal.
Dit maakt duidelijk dat het helemaal niet moeilijk is om structuur informatie te verliezen als men louter op getallen geconcentreerd blijft.
Met een vector die voorgesteld wordt als bitstring construeren we een matrix die met die vector gerelateerd is. Die matrix begrijpen we als een 1-splitsing. Op hun beurt kunnen complexe en perplexe getallen evenzeer als een 1-splitsing begrepen worden.
Dit betekent dat de inherente tweeledigheid die zo duidelijk naar voor komt in het haakformalisme gemakkelijk verloren raakt door wiskundige technieken te gebruiken die verder niet onderzocht worden in functie van operationeel te onderbouwen uitspraken. De perplexe getallen die in het haakformalisme juist dezelfde tweeledigheid duidelijk maken onderstrepen dit met klem.
De eigenwaarde van een operator die een vector kan transformeren is de factor waarmee de grootte van een bepaalde vector door de transformatie geschaald wordt. De projectoren die geconstrueerd worden met het uitwendig product in het 1-splitsing universum hebben voor elke vector waarop ze inwerken één eigenwaarde die verschillend is van nul. Hiermee komt een eigenvector overeen die een afbeelding is van de vector die de projector construeerde met een factor (1+i) of (1+j).
Met behulp van een exploratie in het twee-onderscheidingen universum tonen we aan dat elke projector (die opgebouwd is als uitwendig product van een vector met zichzelf, vector die opgebouwd werd op basis van onderscheidingen) elke vector van de tralie zal projecteren op zijn eigen vector, gewogen met een reële factor. Deze vector is de eigenvector van de lineaire transformatie en is een vector waarvan de richting niet veranderd wordt door de transformatie. Richting betekent dat het patroon van hoog-laag bits wordt behouden, in tegenstelling met de andere vectoren van de tralie waarvan het patroon van hoog-laag bits veranderd wordt bij de projectie naar het patroon van de eigenvector.
De getallen die we als factor van de transformatie zullen vinden zijn dus de eigenwaarden van de projectoren. De eigenwaarden zijn volledig bepaald door de tralie waarin ze functioneren en we laten zien in de exploratie in het twee-onderscheidingen universum dat ze het verschil geven van het aantal gelijke bits en het aantal verschillende bits tussen de koppels punten, iets wat we ook bij het inwendig product van vectoren teruggevonden hebben. Niet alle eigenwaarden zijn dus mogelijk, en de verzameling van mogelijke eigenwaarden van een projector wordt het spectrum van de projector genoemd. Dit spectrum komt dus overeen met de afstanden die in de tralie mogelijk zijn tussen de verschillende niveaus.