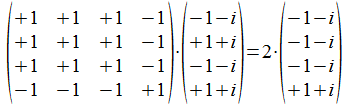
De actie van projector Pab (of ook P<ab>) op a

Tussen 1000 (dus ab) en 1010 (dus a) is het aantal bits gelijk 3, aantal bits verschillend is 1, het verschil is 2. We kunnen dit ook als volgt interpreteren: dit is de vector <ab> met de factor -2. Inderdaad: 0111 en 1010: het aantal bits gelijk is 1, het aantal bits verschillend is 3, het verschil is -2.
Omgekeerd: de actie van projector Pa (of ook P<a>) op ab
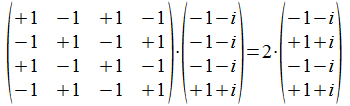
Tussen 1010 (dus a) en 1000 (dus ab) is het aantal bits gelijk 3, aantal bits verschillend is 1, het verschil is 2. We kunnen dit ook als volgt interpreteren: dit is de vector <a> met de factor -2. Inderdaad: 0101 en 0111: het aantal bits gelijk is 1, het aantal bits verschillend is 3, het verschil is -2.
De actie van ervaren projector Pa↔<> op ab
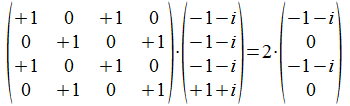
Het resultaat is ervaren vector a met coëfficiënt 2. Maar eigenlijk is dit een brug te ver: is a ervaren dan MOET ab ervaren zijn! Dus door gebruik te maken van wat we reeds weten van het haakformalisme moeten we noteren:
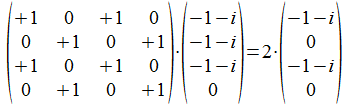
We zien dat dit inderdaad geen verschil maakt.
We merken nu op: het aantal bits gelijk tussen x000 en x0x0 is 2 en het aantal bits verschillend is 0. Blijkbaar geldt dus dat de positie waar een van beide een x vertoont niet mee verrekend wordt.
De projectoren voor ervaren punten zijn niet gelijk met de projectoren voor de ervaring inbedding van het punt. We onderzoeken nu de actie van de ervaren projector P<a>↔<> op ab.
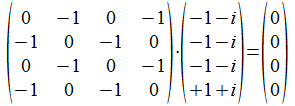
1x0x en 0x0x hebben 1 bit gelijk en 1 bit verschillend. De twee posities waar beide een x vertonen tellen niet mee.
De selectie van een ervaren atoom projector is natuurlijk ook een voorbeeld. Beschouw de ervaren projector voor een van de atomen (P<<a><b>>↔<> of P<a><b>↔<<>>) agerend op a:

We kunnen ook actie onderzoeken van de projector Pa (of P<a>) op een ervaren punt.
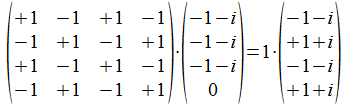
Het resultaat is vector a met factor 1 of vector <a> met factor -1. Geldt de volgende collaps: x000 dan is a waargenomen als x010 en beide punten hebben 2 bits gemeenschappelijk en 1 verschillend, dus 2-1=1 en dan is <a> waargenomen als x101 en beide punten hebben 1 bit gemeenschappelijk en 2 bits verschillend, dus 1-2=-1.
Beschouw terug de ervaren projector voor een van de atomen (P<<a><b>>↔<> of P<a><b>↔<<>>) agerend op a:

Geldt xxx0 dan is 1010 waargenomen als xxx0 en beide hebben een bit gelijk en geen verschillend. Ook hier geldt dat als <<a><b>> ervaren is ook a ervaren MOET zijn, en leidt tot hetzelfde resultaat.
