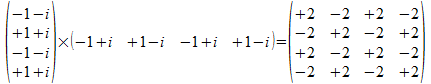
Operatoren P die vermenigvuldigd met zichzelf als resultaat de operator zelf geven zijn idempotent, met andere woorden als P²=P, dan is P idempotent. Een operator P is dus idempotent indien voor de componenten van de matrixvoorstelling P_ij geldt dat Σ_jP_ijP_jk=P_ik. Operatoren die idempotente operatoren zijn, worden projectoren genoemd en zullen hierdoor voor de operatie (in dit geval het matrix product) de functie van eenheid innemen. Projectoren zijn dan ook commutatief.

Met behulp van een concreet voorbeeld uit het twee onderscheidingen universum tonen we aan dat operatoren projectoren zijn, als ze gevormd worden door het uitwendig product in het 1-splitsing universum van een haakvector met zichzelf.

We construeren eerst de operator die vanuit het uitwendig product gevormd wordt van a met zichzelf in een twee onderscheidingen universum, we noemen die operator P_a of in Dirac notatie |a><a| .

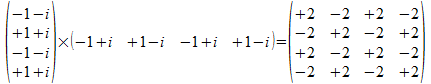
We berekenen nu P_a².

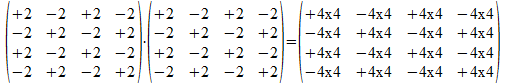
Als we de vectoren met 2^-3/2 vermenigvuldigen dan worden de operatoren met 2^-3 vermenigvuldigd, ze hebben dus coëfficiënt 2^-2 (in plaats van de in de matrix P_a vermelde 2), dan wordt het resultaat van de vermenigvuldiging van de operatoren met 2^-6 vermenigvuldigd en is de coëfficiënt van het resultaat 2^-62⁴ = 2^-2 . We merken dus dat het resultaat de operator P_a zelf is. Expliciet dus:

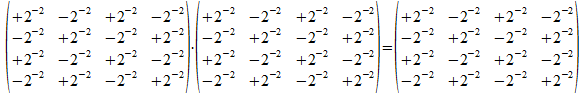
QED

Dit kan op een voor de hand liggende manier uitgebreid worden naar een n onderscheidingen universum voorgesteld als 1-splitsing. Voor een n onderscheidingen universum geldt in het algemeen: als we de vectoren met 2^-(1/2)(n+1) vermenigvuldigen dan worden de operatoren met 2^-(n+1) vermenigvuldigd, ze hebben dus coëfficiënt 2^-n (in plaats van de in de matrix vermelde 2), dan wordt het resultaat van de vermenigvuldiging van de operatoren met 2^-2(n+1) vermenigvuldigd en is de coëfficiënt van het resultaat 2^-2(n+1)2⁽ⁿ⁺²⁾ = 2^-n . We merken dus dat het resultaat de operator zelf is.

Besluit: projectoren als afbeelding voor alle haakvectoren

We merken op dat de constructie van de operator langs complexe getallen kan, zoals hier uitgevoerd, maar ook langs perplexe getallen. Met behulp van de perplexe getallen hebben we aangetoond welke rol de coëfficiënten van het “reëel” en “perplex” deel spelen bij de normalisatie.

We bewijzen dat de constructie van de operator eveneens langs reële getallen kan uitgevoerd worden als ook daar adequate normalisaties uitgevoerd worden. Inderdaad het uitwendig product van (-1 +1 -1 +1)^T en (-1 +1 -1 +1) is hetzelfde soort operator in de grondvorm als met de complexe getallen, maar dan met andere normalisatie factoren wanneer we willen dat de operator een projector is. Ook hier wordt dan duidelijk welke rol andere getallen in de vector uitdrukking spelen bij de normalisatie, en dus hoe structuurinformatie hieruit kan afgeleid worden.

De projectoren kunnen dus als onafhankelijke afbeelding van haakvectoren in het getallendomein onderzocht worden en hierbij zullen de grondvormen een belangrijke rol spelen.