Analoog met de opbouw die we gevolg hebben voor de afbeelding op complexe getallen kan ook het isomorfisme met de perplexe getallen opgebouwd worden: de compatibiliteit met het modulo 3 formalisme, de inwendig en uitwendig producten en de normalisatie.
We beperken ons daarom tot een aantal voorbeelden die duidelijk maken dat inwendig product en uitwendig product dezelfde basisvormen hebben als in het geval van de complexe interpretatie, enkel de normalisatiefactoren verschillen. De normalisatie factoren leiden we dan af door gebruik te maken van coëfficiënten x en y voor de getallen 1 en j om niet in de val te lopen van de oppervlakkige gelijkenis dat 1-1=0, een interpretatie die enkel maar zin heeft als we zouden “vergeten” dat 1 iets anders is dan j. We kunnen de afleiding dan probleemloos volgen er aan denkend dat we x de waarde 1 geven, en ook dat we y de waarde 1 geven. Op deze manier is heel dit proces heel transparant.
Bijvoorbeeld: het inwendig product van <<>> (en <>) in het 1-splitsing universum is
![]()
Het uitwendig product levert de operator op
![]()
Normalisatie levert de eenheid op voor het inwendig product.
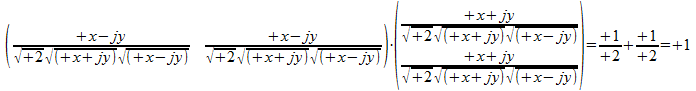
Dit leidt bijvoorbeeld tot een atoom operator in het twee onderscheidingen universum met de gepaste normalisatiefactor:
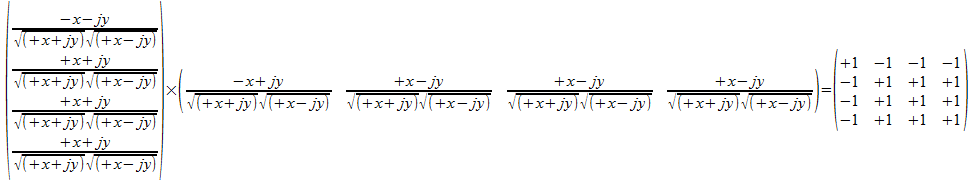
We zullen de onderzoeken naar de resulterende structuren die in het complexe geval uitgevoerd werden kunnen overnemen, rekening houdend met aangepaste normalisatiefactoren.