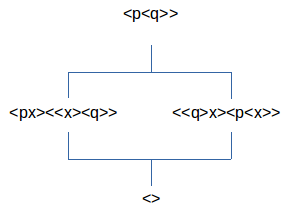
We construeren de conjunctie van <p>x (x is fijner dan p) en <x>q (q is fijner dan x), namelijk <<<p>x><<x>q>>. We herkennen het patroon van een creatief product waarbij de toegevoegde onderscheiding x is en dit is niet anders dan <px><<x><q>> of (<p>⊗q)_x. Het interval omvat zowel p als q, inderdaad indien er geen verschil is tussen p en x dan wordt <p>q bekomen, en eveneens wordt <p>q bekomen indien er geen verschil is tussen x en q, en de uitdrukking <p>q is de uitdrukking dat q fijner is dan p. Dus dat is een interval voor de relatie van simultaneïteit: x bevindt zich in de relatie van simultaneïteit tussen p (supremum) en q (infimum). Inderdaad, het supremum is <<p><q>> en dit is niet anders dan p, het infimum is pq en dat is niet anders dan q. Bewijs: uit <p>q↔<> volgen: <<p>q>↔<<>>, <<p><q>><<p>q>↔<<p><q>>, <<<<p><q>><<p>q>>>↔<<p><q>>, <<p><<<q>><q>>>↔<<p><q>>, <<p><q<q>>>↔<<p><q>>, <<p><<>>>↔<<p><q>>, p↔<<p><q>>, en ook volgt uit <<p>q>↔<<>>, <<p>q>q↔q, <<p>>q↔q, pq↔q, QED.

Dit geldt voor gelijk welke keuze van punten uit een tralie dus een toegevoegde onderscheiding zal in de tralie meer niveaus creëren. We merken ook op dat de constructie duidelijk maakt dat x, p en q niet op hetzelfde niveau staan. Alle drie zijn het welgevormde haakuitdrukkingen, maar ze kunnen niet alle drie onafhankelijke onderscheidingen zijn in één en hetzelfde universum. Een noodzakelijke en voldoende voorwaarde voor de strikte ordening van “x tussen p en q”, is dat x in een groter universum uitgedrukt moet worden dan p of q.

De toegevoegde welgevormde haakuitdrukking bevindt zich dus tussen p en q, het creatief product zelf (dus <px><<x><q>>) bevindt zich tussen de conjunctie en de disjunctie van de termen. De termen zijn in dit geval <p> en q. In dit geval is dus de conjunctie <p<q>> en de disjunctie <p>q, die, in de veronderstelling van de constructie, niet verschillend is van <>. Hetzelfde geldt natuurlijk ook voor (q⊗<p>)_x of dus <<q>x><p<x>>.

Het interval kan verder gestructureerd worden door de relatie van simultaneïteit. Inderdaad, veronderstel twee onderscheidingen met de relatie <x₁>x₂. We veronderstellen de conjunctie <<<p>x₁><<x₁>q>>.We construeren nu de conjunctie van <x₁>x₂ (x₂ is fijner dan x₁) en <x₂>q (q is fijner dan x₂): <<<x₁>x₂><<x₂>q>>. De conjunctie van beide conjuncties samen geeft <<<p>x₁><<x₁>q><<x₁>x₂><<x₂>q>>. We kunnen dat vereenvoudigen naar de uitdrukking <<<p>x₁><<x₁>x₂><<x₂>q>> door toepassing van de transitiviteit van de relatie van simultaneïteit, of door voor alle mogelijkheden te tonen dat beide uitdrukkingen dezelfde waarde hebben zoals in onderstaande tabel.

Deze tabel maakt ook duidelijk dat een simultaneïteitsinterval in de standaard taal uitgedrukt wordt door: indien het supremum van het interval, of het supremum van een deelinterval de waarde <> heeft dan moeten alle fijnere punten de waarde <> hebben wanneer het simultaneïteitsinterval de waarde <> heeft. En natuurlijk volledig duaal: indien het infimum van het interval, of het infimum van een deelinterval de waarde <<>> heeft, dan moeten alle ruimere punten de waarde <<>> hebben wanneer het simultaneïteitsinterval de waarde <> heeft.

We kunnen <<<p>x₁><<x₁>x₂><<x₂>q>> ook als volgt schrijven <<<p>x₁><<x₁>x₂><<x₁>x₂><<x₂>q>> zodanig dat duidelijk wordt dat er geldt: <<<p>x₁><<x₁>x₂><<x₂>q>>↔<(p⊗<x₂>)_x1(x₁⊗<q>)_x2>. Dit is dus de inbedding van een nevenschikking. Als de twee termen van de nevenschikking elkaar uitsluiten is de nevenschikking niet te onderscheiden van het vectorproduct en dan is de operatie niet te onderscheiden van een creatief product. Welk creatief product is dat dan?

Als beide elkaar uitsluiten dan is de conjunctie van <<p>x₁><<x₁>x₂> en <<x₁>x₂><<x₂>q> gelijk aan <<>>. We drukken dat dus uit in een welgevormde haakuitdrukking die een waarde krijgt:

<<<<p>x₁><<x₁>x₂>><<<x₁>x₂><<x₂>q>>>↔<<>>

<<<<p>x₁>><<<x₂>q>>><<x₁>x₂>↔<<>>

<<p>x₁<x₂>q><<x₁>x₂>↔<<>>

Dit is enkel mogelijk wanneer beide volgende voorwaarden voldaan zijn: <<p>x₁<x₂>q>↔<<>> en <<x₁>x₂>↔<<>>. Een voldoende voorwaarde hiervoor is dan dat x₁ en x₂ dezelfde waarde hebben die verder niet gekend is. Dit is belangrijk voor de volgende reden: het is altijd mogelijk om uit te drukken dat de toestanden x_i dezelfde waarde hebben, hoe uitgebreid we i ook nemen. Dit is echter niet zo wanneer we zouden willen uitdrukken dat toestanden een tegengestelde waarde hebben, dat kan niet zomaar voor meer dan twee toestanden. Geef nu die onderscheiding de naam a, dan geldt dat (p⊗<x₂>)_x1(x₁⊗<q>)_x2∼(p⊗<a>)_a(a⊗<q>)_a↔((p⊗<a>)_a⊗(a⊗<q>)_a)_a

Uiteraard is de uitdrukking <<<p>x₁><<x₁>x₂><<x₂>q>> ook uit te breiden naar <<<p>x₁><<x₁>x₂><<x₂>x₃><<x₃>q>> enz…

Uiteraard zijn er verschillende intervallen mogelijk tussen p en q. Zij kunnen intervallen zijn van een volledige tralie met p als extremum en q als infimum. Veronderstel nu dat p het ultieme supremum is, namelijk <<>>, dan wordt het interval de zeer uitgebreide totale ordening <<<x₁>x₂><<x₂>x₃>...<<x_i>x_i+1>...<<x_n>q>> gerelateerd met de inbedding hiervan: <<x₁>x₂><<x₂>x₃>...<<x_i>x_i+1>...<<x_n>q>. En natuurlijk geldt dit ook voor q als ultieme infimum wat de uitdrukking oplevert <<<p>x₁><<x₁>x₂><<x₂>x₃>...<<x_i>x_i+1>> met de inbedding hiervan: <<p>x₁><<x₁>x₂><<x₂>x₃>...<<x_i>x_i+1>. De twee veronderstellingen leiden dan tot <<x₁>x₂><<x₂>x₃>...<<x_i>x_i+1>. Het aantal i geeft dan het aantal niveaus tussen <<>> en <> en er is slechts één x_i op elk niveau. Dit maakt duidelijk dat elke tralie zoveel soorten simultaneïteit kan representeren als er punten zijn op centraal niveau (bijvoorbeeld: neem p en q als de extrema in twee onderscheidingen dan zullen we 6 intervallen tussen p en q kunnen onderscheiden).

Uiteraard kan het ook dat de intervallen geen onderlinge relaties hebben behalve de extrema.

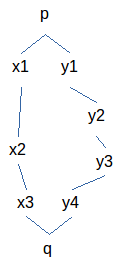
Dit toont de situatie waarbij p niet verschillend is van de conjunctie van <<<p>x₁><<x₁>x₂><<x₂>x₃><<x₃>q>> en <<<p>y₁><<y₁>y₂><<y₂>y₃><<y₃>y₄><<x₄>q>> en dat q niet verschillend is van de disjunctie van <<<p>x₁><<x₁>x₂><<x₂>x₃><<x₃>q>> en <<<p>y₁><<y₁>y₂><<y₂>y₃><<y₃>y₄><<x₄>q>>.