Machtsverheffing is in het algemeen niet commutatief en niet associatief.

De logaritme van x^y is de exponent waartoe de eenheid, het zogenaamde “grondtal” of “basis” x, moet worden verheven om x^y als resultaat te verkrijgen en is dus een soort invers van x^y. De operatie “logaritme” is dus altijd verbonden met een bepaald grondtal en dat wordt genoteerd als log_x. Er geldt dus als definitie van de operatie: log_x(x^y)=y. Elk positief getal kan als eenheid (grondtal) genomen worden. Het getal 1 neemt dan een speciale plaats in want voor elke keuze van exponent is het resultaat van de operatie gelijk aan 1. Het getal 1 is dus dominant (opslorpend) voor de operatie. Een grondtal dat de eenheid is van de logaritme en verschillende resultaten kan opleveren zal dus altijd moeten afwijken van 1. Dit grondtal kunnen we dus schrijven als (1+k) voor gelijk welke positieve k of (1-k) met dan de bijkomende voorwaarde dat de positieve k groter is dan nul en kleiner dan 1 want de logaritme is niet gedefinieerd voor negatieve grondtallen of negatieve getallen. Negatieve getallen kunnen altijd als complexe getallen voorgesteld worden (want -1=e^πi) en elk complex getal heeft een onbepaald aantal logaritmes (van elkaar verschillend op een geheel veelvoud van 2πi na).

Elk positief getal x heeft een logaritme in elk grondtal en een willekeurig grondtal kan altijd gekozen worden binnen de hierboven geformuleerde restricties. Elk positief getal x heeft dus een onbekend aantal inversen. De intensiteit van een gekozen grondtal b (basis, grondtal, eenheid) is dus de exponent c waartoe het grondtal moet verheven worden om x te bekomen. Dus: kies een grondtal b, dan is per definitie log_b(x)=c dan en slechts dan wanneer x=b^c. Dit kunnen we dus ook altijd schrijven als x=(1±k)^c (met 0<k<1) waarbij het grondgetal 0 en het grondtal 2 dan limietvormen zijn.

Wanneer we de operatie log_b nu afkorten tot Lb dan kunnen we noteren: x=b^Lb(x). Neem nu een ander grondtal g en kort de logaritme operatie af tot Lg dan is datzelfde getal x niet anders dan x=g^Lg(x). Dit geeft dan de mogelijkheid om logaritmes met elkaar te relateren. Dus b^Lb(x)=g^Lg(x). Dus 1=b^Lb(x)/g^Lg(x). Dit is een verhouding en definieert dus de eenheid 1 voor twee keuzen: b en g, of dus (1±k_b) en (1±k_g).

Nu merken we op dat 1 op verschillende manier kan gedefinieerd worden. We starten daarom terug met a=b^Lb(a). Neem nu de logaritme La van deze gelijkheid (we korten log_a nu af tot La) en we merken op dat La(a) gelijk is aan 1 (de exponent van a die resulteert in a): 1=La(a)=La(b^Lb(a))=Lb(a)La(b). Dit is een verhouding en dit definieert dus de eenheid 1 voor twee keuzen: a en b. Dus La(b)=1/Lb(a) en Lb(a)=1/La(b). Dat kunnen we ook noteren als log_(1±kb)(1±k_a)=1/log_(1±ka)(1±k_b). Dit kan verder uitgebreid worden. Neem a=b^Lb(a). Neem nu de logaritme Lc van deze gelijkheid: Lc(a)=Lc(b^Lb(a))=Lb(a)Lc(b). Dit is een verhouding en dit definieert dus de eenheid 1, namelijk 1=Lb(a)Lc(b)/Lc(a) voor drie keuzen: a, b en c. Dit kan uiteraard verder uitgebreid worden, bijvoorbeeld met een grondtal d en een logaritme Ld. Neem dan b=d^Ld(b) en dus Lc(b)=Ld(b)Lc(d) en dus is Lc(a)=Lb(a)Lc(b)=Lb(a)Ld(b)Lc(d). Dit is gemakkelijker te interpreteren als het volgende patroon: Lc(a)=Lc(d)Ld(b)Lb(a). Zoals de vergelijking nu geschreven is begint het linker lid met het symbool Lc, de soort operatie en eindigt met het symbool (a), het getal waarop de operatie inwerkt. Het rechter lid laten we ook beginnen met het symbool Lc en eindigen we met het symbool (a) en hiertussen vullen we hetzelfde patroon in. Dit is terug een verhouding en dit definieert dus de eenheid 1 voor vier keuzen: a, b, c en d.

Het patroon dat we zien verschijnen is het patroon van een creatief product waarbij (a⊗b⊗...⊗c)_ℵ niet anders is dan (a⊗c)_ℵ.

Dit patroon vinden we ook als volgt terug:

x=a^La(x) per definitie

Nu construeren we een exponent met grondtal a en term y

x^La(y)=(a^La(x))^La(y)=a^La(x)La(y)

Dit schrijven we nu als

x^La(y)=(a^La(y))^La(x)

Dus het resultaat hiervan is niet anders dan x^La(y)=y^La(x) want per definitie geldt dat y=a^La(y).

We maken dus een keuze van grondtal (eenheid) en dan kiezen we een getal y in de termen van de exponent, termen die allemaal gelijkwaardig zijn en we kunnen dit altijd uitbreiden tot a^{La(x)La(y)La(z)...La(ℵ)}

Hierbij geldt dat x^La(y)=y^{La(x)La(z)...La(ℵ)} en x^La(z)=z^{La(x)La(y)...La(ℵ)} enz…

Het is die gelijkwaardigheid van termen in de exponent die de betekenis is van de laatst toegevoegde onderscheiding in het getallendomein. De laatst toegevoegde onderscheiding in het getallendomein kan gelijk welk getal zijn en dit komt overeen met het inzicht dat we de vrije keuze hebben van de grootte van het onderscheidingen universum waarmee we de werkelijkheid opspannen. Die grootte is enkel naar boven begrensd, wat we interpreteren als de grens die we onvermijdelijk moeten aanvaarden bij de constructie van een causale ordening (de betekenis van “laatste”): een mogelijk verleden en een mogelijke toekomst. Bij de extrema gaat de ordening verloren. Dit is de operationele betekenis van “idempotentie” en “oneindig” in een onvermijdelijk beperkt universum: zeer groot en onwaarneembaar groter, zoals bij een weegschaal met een maximum bereik van 5 kg waar alle gewichten hoger dan 5 Kg niet meer kunnen geordend worden door de meting ervan door een agens met behulp van die weegschaal (voor deze operatie uitgevoerd door een agens-in-context is dus 5 niet anders dan oneindig in die context) en waarbij er ook een ondergrens is voor een gewicht dat die weegschaal kan beïnvloeden.

De betekenis van de getallen 0 en 1

In het getallendomein komt de machtsverheffing overeen met het creatief product. Als machtsverheffing associatief is komt dit overeen met een creatief product met een laatst toegevoegde onderscheiding, genoteerd als (x⊗y)_ℵ. De laatst toegevoegde onderscheiding wordt dan niet ingebouwd in de tralie. Het creatief product heeft dan maximaal twee elementen: een element x en een element y. Een van de elementen neemt de rol in van eenheid, het andere element neemt de rol van intensiteit van die eenheid. We kunnen twee keuzen maken voor de notatie van (x⊗y)_ℵ in het getallendomein: x^y of y^x. Beide keuzen zijn even valide. Nemen we de keuze voor x^y dan construeren we x door (x^y)^1/y en dan construeren we y door Lx(x^y). Voor de machtsverheffing kunnen 0 en 1 als exponent gekozen worden en de keuze als grondgetal genereert idempotentie. Noteer dat (X⊗y)_ℵ altijd gedefinieerd is met X de al-nul vector en X is altijd te construeren door de vectorsom <x>⊕x, som die distributief is met het creatief product (x⊗y)_ℵ=x⊕(X⊗(<x>⊕y))_ℵ.

We zullen nu aantonen dat we een bekende eigenschap van het creatief product enkel kunnen terugvinden in het geval we voor zowel x als y het getal 1 kiezen.

Wanneer we (x⊗y)_ℵ noteren als de operatie a en (y⊗x)_ℵ noteren als a^-1 waarbij (a⊗a^-1)_ℵ=x en (a^-1⊗a)_ℵ=y met x en y de eenheid van de operatie, dan hebben we bewezen dat de nevenschikking aa^-1 niet verschillend is van het vectorproduct a•a^-1, zoals bij elk creatief product en dat de laatst toegevoegde onderscheiding noodzakelijkerwijze geïmpliceerd wordt in de operatie maar in het resultaat niet zichtbaar is. Inderdaad, de nevenschikking (x⊗y)_ℵ(y⊗x)_ℵ is <ℵ<x>><<ℵ><y>><ℵ<y>><<ℵ><x>> en herschikking levert <ℵ<x>><<ℵ><x>><ℵ<y>><<ℵ><y>> of dus xy en hierbij is ℵ “verdwenen”, in het getallendomein komt dat overeen met een 1 (die niet genoteerd moet worden).

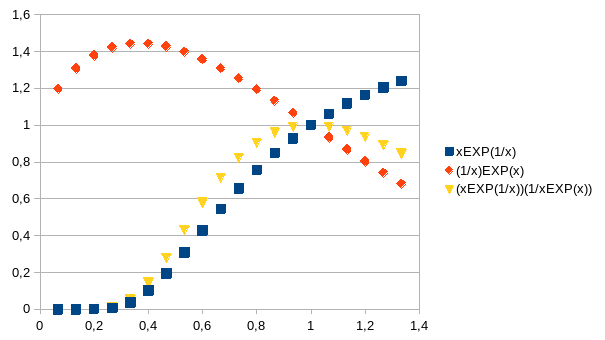
We kunnen de coherentie van dit resultaat verder onderzoeken. We noteren de machtsverheffing als: (x⊗y)_ℵ∼x^y en (y⊗x)_ℵ∼y^x. de nevenschikking xy (met onzichtbare laatst toegevoegde onderscheiding) zou dan moeten overeenkomen met het getalproduct x^yy^x als intensiteit van de eenheid 1 die onzichtbaar is en ook met het getalproduct xy. We bekijken nu x en y als het invers berekend als de logaritme van de machtsverheffing. Als we de logaritme in de basis x noteren als Lx en de logaritme in de basis y noteren als Ly dan geldt dat Lx(y)Ly(x)=1. Inderdaad: start met de definitie zelf van logaritme x=y^Ly(x). Neem nu de logaritme Lx van deze gelijkheid en we merken op dat Lx(x) gelijk is aan 1 (de exponent van x die resulteert in x): 1=Lx(x)=Lx(y^Ly(x))=Ly(x)Lx(y). Hieruit volgt dat 1=xy, het product van x en y. Dus y kan niet anders zijn dan 1/x en geen van beide kan 0 zijn. Dan volgt dat de gelijkheid van x^yy^x met xy (dus voor getallen als eenheid) enkel mogelijk is voor x=y=1, wat gedemonstreerd wordt in onderstaande grafiek waarin we x^1/x en (1/x)^x en hun product voorstellen.

Besluit: eenheid en intensiteit

De eenheid die we vrij kunnen kiezen als grondtal van machtsverheffing moet verschillend zijn van 1 om de operatie van machtsverheffing zin te geven. Dit grondtal kunnen we dus schrijven als (1+k) voor gelijk welke positieve k of ook als (1-k) met de bijkomende voorwaarde dat de positieve k groter is dan nul en kleiner dan 1.

Het grondtal (als eenheid van de machtsverheffing) moet dus minstens een dubbelgetal zijn. Elk dubbelgetal a±b met a groter dan b is te schrijven als a(1±b/a) waarbij b/a voldoet aan de voorwaarde 0<b/a<1 en dit zorgt dus voor een 0<k<1. Hierbij is a dus de grootste intensiteit van de eenheid (1±b/a). Dus a bepaalt de schaal van de eenheid.

De eenheid van de machtsverheffing kan tot een exponent verheven worden en de exponent is dan de intensiteit. De exponent in de machtsverheffing (de intensiteit van de machtsverheffing) kan zowel een getal of een dubbelgetal zijn, inderdaad: (1±k)^(a±b) (met 0<k<1) is niet anders dan (1±k)^a ×(1±k)^±b. De intensiteit kan een product zijn, en dan kan elke term van het product de laatst toegevoegde zijn, bijvoorbeeld (1±k)^(a±b)(c±d) kunnen we schrijven als ((1±k)^(a±b))^(c±d) maar ook als ((1±k)^(c±d))^(a±b).

Elk getal kan de rol van intensiteit spelen voor elke operatie (som, product, machtsverheffing en tetratie), maar enkel een dubbelgetal kan de rol van eenheid spelen voor elk van de volgende operaties: som, product, machtsverheffing en tetratie.

De exponent is altijd een intensiteit, geen eenheid, is altijd een dimensieloos getal. Dat is het snelst in te zien door een willekeurig getal te schrijven als e^x en dit, met het inzicht van Euler, te schrijven als een niet eindigende som van hogere machten van x. Die machten kunnen daardoor geen dimensionale betekenis hebben. Dus e^x = Σ_k=0(x^k)/k! , of dus de som 1+(x)¹/1!+(x²)/2!+(x³)/3!+(x⁴)/4!+… en als x de dimensie afstand zou hebben, is het zinloos om daar een oppervlak, een volume enz… bij op te tellen.