Indien het product van twee operaties als resultaat de eenheid geeft dan worden die operaties elkaars invers genoemd. Het creatief kwadraat maakt duidelijk dat het creatief product twee eenheden heeft.

Dit speelt natuurlijk een rol in het creatief product van een creatief product. In het algemeen hebben we bewezen dat ((x⊗a)_ℵ ⊗(b⊗y)_ℵ)_ℵ niet te onderscheiden is van (x⊗y)_ℵ. Nu gaan we daar dieper op in.

Enkelvoudige operatie

We zullen eerst bewijzen dat (x⊗y)_ℵ en (y⊗x)_ℵ elkaars invers zijn ten opzichte van de eenheid x voor het creatief product. We zullen dus bewijzen dat ((x⊗y)_ℵ ⊗ (y⊗x)_ℵ)_ℵ niet verschillend is van de eenheid x.

Bewijs

<ℵ<x>><<ℵ><y>> vermenigvuldigen met <ℵ<y>><<ℵ><x>> met behulp van de laatst toegevoegde onderscheiding geeft als welgevormde haakuitdrukking:

<ℵ<<ℵ<x>><<ℵ><y>>>><<ℵ><<ℵ<y>><<ℵ><x>>>>

<ℵ<<<x>><<><y>>>><<ℵ><<<><y>><<x>>>>

<ℵ<<<x>>>><<ℵ><<<x>>>>

<ℵ<x>><<ℵ><x>>

<<x><<ℵ><<ℵ>>>>

x

QED

Merk op dat dit volledig onafhankelijk is van de laatst toegevoegde onderscheiding, of deze zich nu op centraal niveau bevindt of niet (en dus als onderscheiding kan gebruikt worden), of deze nu een waarde heeft of niet doet er niet toe.

Volledig analoog bewijzen we dat (y⊗x)_ℵ en (x⊗y)_ℵ elkaars invers zijn ten opzichte van de eenheid y. Het creatief product heeft dus twee eenheden. Noteer dat we hiermee ook impliciet de associativiteit bewezen hebben.

Conventioneel kunnen we (x⊗y)_ℵ noteren als de operatie a en (y⊗x)_ℵ noteren als a^-1 waarbij (a⊗a^-1)_ℵ=x en (a^-1⊗a)_ℵ=y. Hierbij is x de eenheid van de operatie a en y de eenheid van de operatie a^-1.

Elke eenheid is eveneens als een operatie te noteren door een waarde toe te kennen aan de toegevoegde onderscheiding, namelijk x is de operatie (x⊗y)_<<>> want <<<>><x>><<><y>> is x, natuurlijk geldt dit ook voor (y⊗x)_<>. En y is (x⊗y)_<> en dus ook (y⊗x)_<<>>.

Een speciaal geval is natuurlijk als een van de twee eenheden de waarde <<>> krijgt, de eenheid van het vectorproduct, waarbij (a⊗a^-1)_ℵ=<<>> en (a^-1⊗a)_ℵ=z als een mogelijkheid. Uiteraard kunnen de twee eenheden dezelfde zijn met waarde <<>> en dan geldt (<<>>⊗<<>>)_ℵ=(a⊗a^-1)_ℵ=<<>> en (a^-1⊗a)_ℵ=<<>>.

Meervoudige operatie

Stel a=(x⊗y)_ℵ en b=(u⊗v)_ℵ

Dus a^-1 noteren we als (y⊗x)_ℵ het invers ten opzichte van eenheid x

Dus b^-1 noteren we als (v⊗u)_ℵ het invers ten opzichte van eenheid u.

We onderzoeken nu de mogelijke binaire combinaties.

(a⊗b)_ℵ=(x⊗v)_ℵ

(b⊗a)_ℵ=(u⊗y)_ℵ

(a^-1⊗b)_ℵ=(y⊗v)_ℵ

(b⊗a^-1 )_ℵ=(u⊗x)_ℵ

(a⊗b^-1)_ℵ=(x⊗u)_ℵ

(b^-1 ⊗a)_ℵ=(v⊗y)_ℵ

(a^-1⊗b^-1)_ℵ=(y⊗u)_ℵ

(b^-1⊗a^-1)_ℵ=(v⊗x)_ℵ

Nu modelleren we het invers van deze operaties en noteren de gelijkheden

(a⊗b)_ℵ^-1=(v⊗x)_ℵ=(b^-1⊗a^-1)_ℵ

(b⊗a)_ℵ^-1=(y⊗u)_ℵ=(a^-1⊗b^-1)_ℵ

(a^-1⊗b)_ℵ^-1=(v⊗y)_ℵ=(b^-1 ⊗a)_ℵ

(b⊗a^-1 )_ℵ^-1=(x⊗u)_ℵ=(a⊗b^-1)_ℵ

Dit is een opmerkelijk resultaat door de involutie die ontstaat in het creatief product. Maar dit geeft ook de mogelijkheid om te onderzoeken onder welke voorwaarde de involutie niet zou optreden. We geven een voorbeeld: we onderzoeken onder welke voorwaarde geldt: (a⊗b)_ℵ^-1=(a^-1⊗b^-1)_ℵ

We hebben al berekend: (a⊗b)_ℵ^-1 is (v⊗x)_ℵ en (a^-1⊗b^-1)_ℵ=(y⊗u)_ℵ. Dus (v⊗x)_ℵ en (y⊗u)_ℵ zijn niet te onderscheiden op voorwaarde dat er geldt: y=v zowel als u=x, dus zowel y•v=<<>> als x•u=<<>> (deze veronderstelling moeten we uitdrukken als een disjunctie die de waarde <<>> heeft, namelijk <y<v>><v<y>><x<u>><u<x>> ↔ <<>>, en natuurlijk geldt dan ook dat de conjunctie de waarde <> heeft, namelijk <<y<v>><v<y>><x<u>><u<x>>> ↔ <>). Omdat we veronderstelden dat er geldt dat a=(x⊗y)_ℵ en b=(u⊗v)_ℵ betekent dit dus dat a en b zich niet onderscheiden, dus a•b=<<>>. Maar dat betekent niet dat de termen x en y gelijk moeten zijn aan elkaar, ze zijn wel gerelateerd. Bijvoorbeeld: a=(c⊗<c>)_ℵ=ℵ•c=b voldoet aan de voorwaarde waarbij geldt dat (a⊗b)_ℵ^-1=(a^-1⊗b^-1)_ℵ. Dat betekent dat we naast a en b ook een c moeten veronderstellen. Er zijn dus twee mogelijkheden die niet simultaan kunnen voldaan worden maar waarbij geldt dat zowel y•v=<<>> als x•u=<<>>.

Eerste mogelijkheid: x=c=u en dan geldt y=<c>=v.

Tweede mogelijkheid: x=<c>=u en dan geldt y=c=v.

De twee mogelijkheden zijn dus:

a=(c⊗<c>)_ℵ=ℵ•c=b

a=(<c>⊗c)_ℵ=<ℵ•c>=b

Uit de eerste mogelijkheid leiden we af:

b•a=b•(c⊗<c>)_ℵ=ℵ•c•b=<<>> en c•a=c•(c⊗<c>)_ℵ=ℵ=c•b

Uit de tweede mogelijkheid leiden we af:

b•a=b•(<c>⊗c)_ℵ=<ℵ•c•b>=<<>> en c•a=c•(<c>⊗c)_ℵ=<ℵ>=c•b en dit kunnen we ook schrijven als ℵ=<c>•b=<c>•a

Dit kunnen we als volgt interpreteren: a en b onderscheiden zich enkel door de laatst toegevoegde onderscheiding die niet ingebouwd wordt in de eenheid c, dus de intensiteit van c is, in het geval dat a waargenomen wordt, het getal ℵ_a (of <ℵ_a>₎, en, in het geval b waargenomen wordt, het getal ℵ_b (of <ℵ_b>₎. Dit kunnen verschillende getallen zijn, dit kunnen dezelfde getallen zijn, maar ze hebben geen invloed op de eenheid die gemeten wordt, ze zijn de kwantificering van “het gedrag van c”, ze hebben dus dezelfde waarde. De waarde van de getallen (die in dit geval dus dezelfde is) is iets anders dan de getalwaarde (gelijk of verschillend). Dat is dus een waarde die “afhankelijk is van een schaal”, die “op een gelijkwaardige manier gemeten is” maar dan misschien tot een andere uitkomst leidt.

Noteer dat c geen welgevormde haakuitdrukking moet zijn, bijvoorbeeld a=((<>⊕h)⊗<<>⊕h>)_ℵ=ℵ•(<>⊕h)=b verandert niets aan het patroon.

Besluit: de structuur van een groep

Het creatief product met een laatst toegevoegde onderscheiding is associatief. Elke welgevormde haakuitdrukking is zijn eigen eenheid en zijn eigen invers. Het creatief product met een laatst toegevoegde onderscheiding is niet commutatief en beide niet commuterende vormen zijn elkaars invers ten opzichte van een eenheid, een van de termen van het creatief product.

In een universum van onderscheidingen introduceert het creatief product met een laatst toegevoegde onderscheiding dus de structuur van een groep.

Gevolgen

Het uitdrukken van logisch te interpreteren relaties met het creatief product

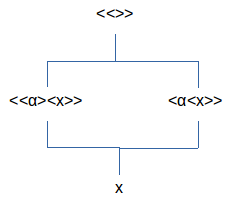
Uit de definitie van invers volgt het speciaal geval dat, indien voor de eenheid de waarde <<>> genomen wordt (de eenheid van de operatie van vectorvermenigvuldiging) (<<>>⊗x)_ℵ en (x⊗<<>>)_ℵ of dus <ℵ<<<>>>><<ℵ><x>> en <ℵ<x>><<ℵ><<<>>>> elkaar invers zijn ten opzichte van <<>>. De welgevormde haakuitdrukkingen kunnen gereduceerd worden tot <<ℵ><x>> en <ℵ<x>> die dus elkaars invers zijn ten opzichte van <<>>. We merken op dat de conjunctie van <<ℵ><x>> en <ℵ<x>> gelijk is aan <<>>.

Exact dezelfde welgevormde haakuitdrukkingen <<ℵ><x>> en <ℵ<x>> zijn dus ook elkaars invers ten opzichte van x, inderdaad de associatieve operatie is dan ((x⊗<<>>)_ℵ⊗(<<>>⊗x)_ℵ)_ℵ. We merken nu op dat x de disjunctie is van <<ℵ><x>> en <ℵ<x>> want er geldt dat <<ℵ><x>><ℵ<x>>↔<<ℵ><x>>•<ℵ<x>>↔x. Aangezien er geldt dat <<ℵ><x>>•<ℵ<x>>↔x, geldt er evenzeer dat <<ℵ><x>>↔x•<ℵ<x>> en ook <ℵ<x>>↔<<ℵ><x>>•x.

Elke welgevormde haakuitdrukking x is dus het vectorproduct van twee uitdrukkingen die elkaars invers zijn ten opzichte van <<>>, en ook ten opzichte van x, afhankelijk van de operatie die gebruikt wordt (conjunctie of disjunctie) om de eenheid te construeren, en dit enkel met de laatst toegevoegde onderscheiding. De vier punten vormen een tralie die af te beelden is op een tralie van 1 onderscheiding.

Het is nuttig dit te vergelijken met het meer algemeen geval waarin we (y⊗x)_ℵ voorstellen en de twee eenheden dus zijn: <<>> en <ℵ<y>><<ℵ><x>>:

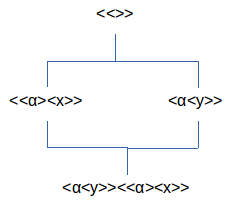
Het patroon (<<>>⊗x)_ℵ is het patroon dat vanuit een atoom, in dit geval gesymboliseerd door x, van een lager onderscheidingen universum een atoom maakt in het universum met toevoeging van ℵ.

In overzicht waarbij we de relatie leggen met andere binaire relaties:

((<<>>⊗x)_ℵ⊗(x⊗<<>>)_ℵ)_ℵ=(<<>>⊗x⊗x⊗<<>>)_ℵ=(<<>>⊗x⊗<<>>)_ℵ=<<>>=<<<<ℵ><x>>><<ℵ<x>>>>=<<>>∼<<ℵ><x>>AND<ℵ<x>> en dit is verschillend van <<ℵ><x>>XNOR<ℵ<x>>

((x⊗<<>>)_ℵ⊗(<<>>⊗x)_ℵ)_ℵ=(x⊗<<>>⊗<<>>⊗x)_ℵ=(x⊗<<>>⊗x)_ℵ=x=<<ℵ><x>><ℵ<x>>↔<<ℵ><x>>•<ℵ<x>>=x∼<<ℵ><x>>OR<ℵ<x>> en dit is niet verschillend van <<ℵ><x>>XOR<ℵ<x>>

Ten opzichte van <> geldt een duale gelijkwaardigheid. We herkennen hierin natuurlijk dat de structuur van een welgevormde haakuitdrukking x (de ene eenheid van het creatief product) in zijn potentiële vorm niet te onderscheiden is van de structuur in zijn ervaren of gebeurde vorm (de andere eenheid van het creatief product).

Vorm een creatief product met een van de AND-atomen en het AND-atoom waarin elke onderscheiding door zijn inbedding is vervangen. Zo’n atomen zijn elkaars invers. Bijvoorbeeld (<ab>⊗<<a><b>>)_c. Dit is niet anders dan <abc><<a><b><c>>. Maar dit is dan ook niet anders dan (<ac>⊗<<a><c>>)_b of (<bc>⊗<<b><c>>)_a. Aangezien de AND-atomen elkaar uitsluiten is <abc><<a><b><c>> niet verschillend van <abc>•<<a><b><c>>. <abc><<a><b><c>>, die niet verschillend is van <abc><<a><b><c>>↔<>, drukt uit dat de drie onderscheidingen dezelfde waarde hebben, die verder niet gekend is.

Het vectorproduct van inversen

We zullen bewijzen dat het vectorproduct van de inversen ten opzichte van het creatief product, namelijk (x⊗y)_ℵ en (y⊗x)_ℵ gelijk is aan het vectorproduct van de termen, namelijk x•y. Dit is dus eveneens onafhankelijk van de laatst toegevoegde onderscheiding ℵ.

Bewijs: we drukken uit wat we willen bewijzen en reduceren die welgevormde haakuitdrukking.

<ℵ<x>><<ℵ><y>>•<ℵ<y>><<ℵ><x>>

<<ℵ<x>><<ℵ><y>><<ℵ<y>><<ℵ><x>>>><<<ℵ<x>><<ℵ><y>>><ℵ<y>><<ℵ><x>>>

<<<ℵ<y><ℵ<x>><<ℵ><y>>><<ℵ><x><ℵ<x>><<ℵ><y>>>>><<<ℵ<x><ℵ<y>><<ℵ><x>>><<ℵ><y><ℵ<y>><<ℵ><x>>>>>

<ℵ<y>x><<ℵ><x>y><ℵ<x>y><<ℵ><y>x>

Dit gaan we herschikken:

<ℵ<y>x><ℵ<x>y><<ℵ><x>y><<ℵ><y>x>

<<<ℵ<y>x><ℵ<x>y>>><<<<ℵ><x>y><<ℵ><y>x>>>

<ℵ<<<y>x><<x>y>>><<ℵ><<<x>y><<y>x>>>

<<<ℵ<<<y>x><<x>y>>><<ℵ><<<x>y><<y>x>>>>>

<<<<y>x><<x>y>><<ℵ><<ℵ>>>>

<<<<y>x><<x>y>><<ℵ>ℵ>>

<<y>x><<x>y>

x•y

QED

Wanneer we (x⊗y)_ℵ noteren als de operatie a en (y⊗x)_ℵ noteren als a^-1 waarbij (a⊗a^-1)_ℵ=x en (a^-1⊗a)_ℵ=y met x en y de eenheid van de operatie, dan is nu duidelijk dat de nevenschikking aa^-1 niet verschillend is van het vectorproduct a•a^-1, zoals bij elk creatief product en dat de laatst toegevoegde onderscheiding noodzakelijkerwijze geïmpliceerd wordt in de operatie maar in het resultaat niet zichtbaar is. Inderdaad, de nevenschikking (x⊗y)_ℵ(y⊗x)_ℵ is <ℵ<x>><<ℵ><y>><ℵ<y>><<ℵ><x>> en herschikking levert <ℵ<x>><<ℵ><x>><ℵ<y>><<ℵ><y>> of dus xy.

In de wereld van getallen kennen we een gelijkaardige associativiteit voor de operatie machtsverheffing.