Simultaneïteitsintervallen in het getallendomein zijn zeer duidelijk en de metriek is goed gekend. Ook de structuur van een tralie vinden we terug in het getallendomein en dat is een fractaal structuur in twee metrische dimensies. De tralie is gebaseerd op priemgetallen en de rol van conjunctie en disjunctie wordt vertaald als de grootste gemene deler en het kleinste gemene veelvoud. We zullen dus dat wat al eeuwen lang gekend is in de getallen op een nieuwe manier interpreteren en dus moeten we dat stap voor stap terug opbouwen.

Hieronder, in het formaat van een 4-hypercube de tralie van 16 punten gevormd door de vier priemgetallen 2, 3, 5 en 7 (die we dus afbeelden op de AND-atomen van een twee onderscheidingen universum), dus tussen 1 als het ene extremum en 2*3*5*7=210 als het andere extremum. Vier willekeurig andere priemgetallen zullen dezelfde structuur genereren. Het aantal priemgetallen beelden we dus af op het aantal toestanden van een onderscheidingen universum (een tralie). We hebben nu voor vier priemgetallen gekozen maar we kunnen gelijk welk aantal priemgetallen kiezen. We stellen een niet gekwantificeerde tralie voor, wat betekent dat geen van de punten een intensiteit (of met andere woorden een bijkomend product of een exponent) heeft:

Hierbij meer gedetailleerd de vertaling van de 16 punten

Hierbij is 1 de grootste gemene deler van de getallen die afgebeeld worden op haakuitdrukkingen die elkaars inbedding zijn. Merk op dat dit geldt voor alle niveaus.

We hebben 4 priemgetallen gebruikt (2, 3, 5, 7) die een structuur opleveren die kan afgebeeld worden op een volledige tralie van onderscheidingen. Maar ook 3 priemgetallen zullen een tralie opspannen. Hieronder een voorbeeld met enkel de priemgetallen (2, 3 en 7) waarbij we de getallen die een vijfvoud zijn in een andere kleur aangeven omdat ze geen deel uitmaken van de gekozen tralie van drie priemgetallen.

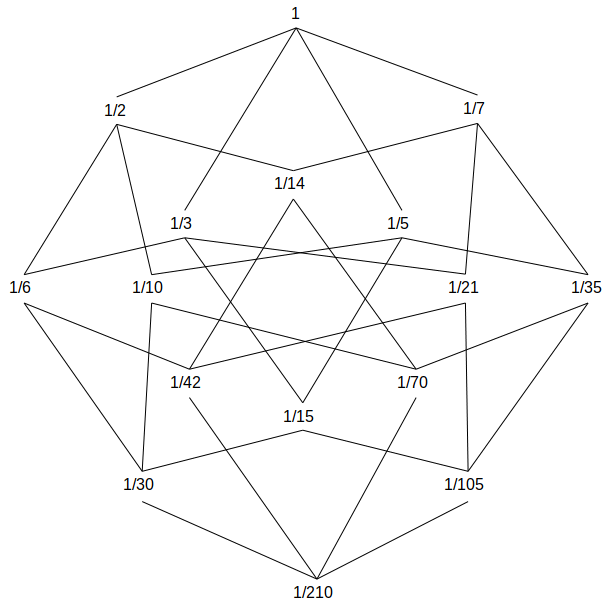
Hiermee ontstaat dus een nieuwe interpretatie van inbedding, verschillend van de modulo2 en modulo3 interpretatie. We kunnen dan een andere afbeelding construeren van inbeddingen in het getallendomein. Daartoe merken we eerst op dat er geen verschil is tussen de structuur van 16 punten met de structuur van de volgende tralie met getallen kleiner dan 1, maar dat beide voorstellingen natuurlijk niet zomaar met elkaar kunnen gemengd worden. De reciproque van een getal wordt soms de kromming genoemd, verwijzend naar de kromming van een cirkel: hoe groter de straal, hoe kleiner de kromming.

Dit maakt duidelijk dat 1/210 de eenheid is van een som van fracties van 1 die opgebouwd worden door de vier priemgetallen 2, 3, 5, 7, namelijk de atomen 2^-1, 3^-1, 5^-1, 7^-1.

Deze tweede vorm maakt duidelijk dat we nu een intensiteit van de hele tralie kunnen veronderstellen. Indien de intensiteit gelijk is aan een van de 16 gehele getallen dan ontstaat een 1 en eventueel ook andere gehele getallen in de tweede vorm. Dit heeft een duidelijke relatie met dubbelgetallen. Om dit te illustreren kiezen we een intensiteit van de volledige tralie overeenkomend met een OR-atoom, zoals de intensiteit 70.

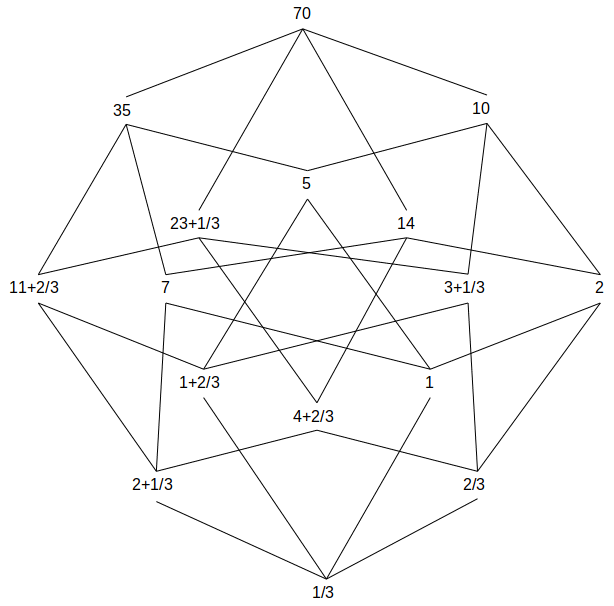
We zien de dubbelgetallen duidelijk weergegeven, het tweede deel van het getal (kleiner dan 1) kan met één breuk weergegeven worden.

We kiezen nu een intensiteit van de volledige tralie overeenkomend met het getal op centraal niveau, zoals de intensiteit 6.

We zien de dubbelgetallen duidelijk weergegeven als 1-1/7 en 1+1/5, de andere getallen kunnen we in dat formaat schrijven door nul te gebruiken. Een van de delen van het dubbelgetal is 1 of een natuurlijk getal groter dan 1. Het tweede deel van het getal is kleiner dan 1 en kan met één breuk weergegeven worden die het product is van twee inverse priemgetallen. Bijvoorbeeld 1/7 is niet anders dan 5/35 en 2/5 is niet anders dan 14/35. Een van de getallen noteren we als 1-1/7 in plaats van 6/7, wat natuurlijk het modulo rekenen illustreert.

Dit maakt onmiddellijk duidelijk dat dit verder uit te breiden is. Als we een intensiteit kiezen overeenkomstig het getal dat een AND-atoom representeert, kan het tweede deel van het getal (kleiner dan 1) dan met één breuk weergegeven worden die het product is van drie inverse priemgetallen.

Al deze patronen zijn uiteraard naar hogere universa uit te breiden en we herkennen de rol van de priemgetallen en hun inversen als de constituerende eenheden die beide een rol spelen in de dubbelgetallen die een tralie kunnen voorstellen.

Dubbelgetallen

We tonen nu aan dat de dubbelgetallen het gevolg zijn van een eigenschap van de grootste gemene deler als eenheid die een intensiteit kan krijgen. We brengen dat aan met een voorbeeld dat gemakkelijk te volgen is en waarvan de abstractie dan voor de hand ligt. Dit is niet anders dan de stelling van Bachet-Bézout die we uitbreiden naar reële getallen, waarbij we duidelijk een verschil zien tussen eenheid (begrensd) en intensiteit (onbegrensd).

We veronderstellen nu twee willekeurige getallen met grootste gemene deler het priemgetal 3, namelijk 3a en 3b. Dus 3 gedraagt zich zoals een gezamenlijke eenheid, vergelijkbaar met het getal 1 (en dus het supremum of infimum van de tralie).

We bewijzen nu dat er altijd een x en een y te vinden zijn met x(3a)+y(3b)=3 waarbij dus x de intensiteit is van de eerste eenheid en y de intensiteit is van de tweede eenheid die dan enkel 3 als gezamenlijke eenheid hebben. We kiezen nu a=10 en b=13 en dus 30x+69y=3.

We substitueren hierin x=x’-2y.

30(x’-2y)+69y=3

30x’-60y+69y=3

30x’+9y=3

Nu voeren we een volgende substitutie door: y=y’-3x’

30x’+9(y’-3x’)=3

30x’+9y’-27x’=3

3x’+9y’=3

Nu volgt een laatste substitutie: x’=x”-3y’

3(x”-3y’)+9y’=3

3x”-9y’+9y’=3

3x”=3

Hieruit volgt

x”=1

We merken nu op dat per constructie y’ gelijk welke waarde kan hebben. We kiezen dus een y’ en berekenen de andere intensiteiten.

Het eenvoudigste voorbeeld is y’=0

Met x’=x”-3y’ volgt x’=1

Met y=y’-3x’ volgt y=-3

Met x=x’-2y volgt x=1+6=7

Dus de twee intensiteiten zijn 30(7)+69(-3)=3

Kiezen we nu y’=1

Met x’=x”-3y’ volgt x’=1-3=-2

Met y=y’-3x’ volgt y=1+6=7

Met x=x’-2y volgt x=-2-14=-16

Dus de twee intensiteiten zijn 30(-16)+69(7)=3

Kiezen we nu y’=1/11

Met x’=x”-3y’ volgt x’=1-3/11=8/11

Met y=y’-3x’ volgt y=1/11-24/11=-23/11

Met x=x’-2y volgt x=8/11+46/11=54/11

Dus de twee intensiteiten zijn 30(54/11)+69(-23/11)=3

We zouden ook kunnen “kiezen” voor y’=1/π

We merken nu op dat met z gelijk welk getal (z)30x+(z)69y=(z)3 dus dit bewijst het universele van deze dubbelgetal constructie, inclusief dus getallen waarvoor we niet kunnen kiezen zoals π en e.

Gevolg

Een priemgetal p wordt gekenmerkt doordat de grootste gemene deler met gelijk welk ander getal het getal 1 is. Er zijn dus altijd twee intensiteiten x en y te vinden zodanig dat (1)x+(p)y=1 en dus ook (1/p)x+(1)y=1/p. Dus 1, p en 1/p zijn als extremum met elkaar gerelateerd en kunnen een tralie opspannen met een specifieke selectie van dubbelgetallen. Aangezien een willekeurig natuurlijk getal als een product van priemgetallen kan voorgesteld worden geldt dat dus voor alle rationale getallen.

Twee getallen die relatief priem zijn spannen een dubbelgetal op dat als eenheid kan gebruikt worden. Neem als voorbeeld (z)30x+(z)69y=(z)3 en deel door (z)3, er geldt 10x+13y=1 en 10 en 13 zijn relatief priem.

Het gevolg hiervan is dat een rationaal getal niet eenduidig bepaald is, neem p/q dan kunnen we dat evenzeer schrijven als zp/zq waarbij z gelijk welk getal kan zijn, een geheel, reëel, dubbelgetal enz...

Eenheid, tralie en rationale getallen zijn dus onlosmakelijk met elkaar verbonden. Intensiteiten zijn intensiteiten van tralies.