Het spontaan gedrag van een entiteit E is een opeenvolging van (elkaar uitsluitende) toestanden (van die entiteit E) waarbij een agens A iets variant waarneemt en simultaan de entiteit E zelf waarneemt en er dus van uit gaat dat dat variante misschien door die entiteit E gekozen wordt zonder dat het de entiteit karakteriseert, maar dat het variante hoe dan ook aan de entiteit E gebeurt. Het agens A komt tot het besluit dat de entiteit E gedrag vertoont. De toestanden zijn aspecten van een proces, een verandering. Bij een waarneming van een aspect van E is dit “ja” en bij een andere waarneming van hetzelfde aspect van dezelfde invariante entiteit is het “neen”. Het proces heeft het spontaan gedrag als waarneembaar spoor bovenop de invariante aanwezigheid van de entiteit E die dat gedrag vertoont. Het waarnemend agens A heeft daar geen invloed op maar kan het spoor wel waarnemen. De toestanden kunnen enkel gebeuren voor het waarnemend agens (en leiden tot zijn/haar waarnemingen). Dit zijn toestanden waarvoor het agens A dus niet kan kiezen omdat het zelf geen deel uitmaakt van het proces (we zeggen met andere woorden dat het zich dus buiten de systeemgrens bevindt van het gedrag dat het wil beschrijven). Het gedrag gebeurt dus aan de entiteit E zowel als aan het waarnemend agens A, maar voor deze laatste slechts met zekerheid tijdens de waarneming van het spoor. De toestanden sluiten elkaar uit zowel voor de entiteit E als het waarnemend agens A. We kunnen er altijd van uitgaan dat het aantal toestanden dat E onvermijdelijk onderscheidt (dus kan en moet onderscheiden) verschillend is van het aantal toestanden dat het waarnemend agens A onderscheidt (dus kan en moet onderscheiden). Dat zal niet verhinderen dat ze tot dezelfde conclusie kunnen komen over de aanwezigheid van E, wellicht met andere onderscheiden aspecten van het gedrag van E.

Trilling

We hebben gezien dat gedrag altijd met trillingen te modelleren is, ze zijn de fysische uiting “ja” versus “neen” van het waarnemen, van “ja” en “neen” is er enkel sprake als iets herhaaldelijk waargenomen wordt. We hebben enkel met “ja” en “neen” ook een “hoek” kunnen definiëren. Een hoek is een interpretatie in geometrische bewoording voor twee getallen die in verhouding tot elkaar staan. Verhoudingen veronderstellen associativiteit en invers en een relatie waarin er geen verschil meer is tussen creatief product, vectorproduct en disjunctie.

Trillingen vinden we ook in de fysische werkelijkheid en daar is dat gerelateerd met golven, hetzelfde geldt voor een hoek die iets cyclisch kan modelleren (het herhaaldelijk waarnemen van hetzelfde). Men zou zich daarom dus kunnen afvragen “wat” er dan trilt of “wat” er dan golft. Inderdaad zijn veel wetenschappers op zoek gegaan naar een ether of een kwantum vacuüm. Met het haakformalisme kunnen we heel duidelijk modelleren wat de vooronderstelling hiervan is zodanig dat beide begrippen minder mysterieus lijken. Daartoe moeten we gedetailleerd en zonder a priori onderzoeken wat door een variërende verhouding gemodelleerd wordt, verhouding die we als variërende hoek en dus als golf willen modelleren. De grote moeilijkheid hierbij is dat we de geometrische interpretatie zoveel mogelijk moeten vermijden. Uiteindelijk kennen we een golf als een verschijnsel in de ruimte-tijd, bij uitstek gerelateerd aan voortplanting van een patroon (dat is een proces) en de voortplantingssnelheid (processnelheid) van een patroon (bijvoorbeeld een geluid, een temperatuur enz…). Het is in het haakformalisme de bedoeling om de vooronderstellingen van de ruimte-tijd te construeren vanuit andere primitieven: het onvermijdelijke dat er ook iets anders gebeurt als we iets doen gebeuren, het “ja” versus “neen” van het waarnemen.

Veronderstel daarom n toestanden (dat zijn dus focuspunten die elkaar uitsluiten zoals bijvoorbeeld sporen van metingen). Het verschil tussen de toestanden zijn (disjuncte) stappen in een proces. We kunnen enkel stappen onderscheiden als er verandering is. De toestanden zijn discontinu juist omdat ze elkaar uitsluiten. De discontinuïteit van de stappen volgt uit de discontinuïteit van de toestanden. Dat betekent dat het onmogelijk is dat het realiseren van een toestand simultaan een andere toestand realiseert. Continuïteit kan enkel een hypothese zijn die zich discontinu manifesteert in de waarneming, waarneming die onvermijdelijk discontinu is juist omdat waarnemingen elkaar uitsluiten, niet simultaan zijn. De disjunctie is in principe onbekend. Dit betekent dat elk agens-in-context niet zekerder kan zijn (anders gezegd: niet “beter kan weten”) dan de hypothesen die het kan construeren met behulp van de toestanden die het kan onderscheiden. De toestanden zijn geordend, wat betekent dat er een toestand eerder ervaren is dan een andere toestand en dat dit geldt voor elke toestand (de duale uitdrukking is dat er een toestand later ervaren is dan een andere en dat dit geldt voor elke toestand). Tot die ordening kan elk agens-in-context besluiten omdat het onvermijdelijk sommige sporen ordent. Het kan dan die ordening gebruiken om gewenste en ongewenste toestanden te kunnen anticiperen.

Veronderstel nu dat een agens die ordening van sporen doorloopt en een parameter vindt waarmee het de stappen (de verschillen van toestanden) kan laten toenemen en blijvend kan laten toenemen met een perfecte additiviteit. We noemen deze variabele n. Die variabele is “stap”, iets dat eigen is aan het waarnemen van elke n, n is een aantal stappen van een concrete agens-in-context. De intensiteit n geeft het aantal doorlopen stappen vanaf een willekeurig gekozen beginpunt. Men kan zich dat dan in een eerste interpretatie als een tijdspanne voorstellen zolang men weerstaat aan de connotatie dat “tijd” los staat van de capaciteiten van het agens-in-context. Dat is een gepaste interpretatie omdat een tijd-afstand enkel kan toenemen in tegenstelling met een ruimte-afstand die kan toenemen en afnemen. Stappen zijn agens-in-context gebonden en zijn discontinu. Stappen zijn onvermijdelijk geordend maar ze zijn niet noodzakelijk even groot. Er is geen verandering wanneer er bij elke stap invariant “ja” waargenomen wordt. Er is slechts verandering wanneer een invariante “ja” plots “iets anders dan ja” of, met andere woorden, een “neen” wordt en dit drukt natuurlijk het onderscheidingsvermogen uit van het agens, “pas dan zet het een stap”. Dit heeft uiteraard zijn duale interpretatie door “ja” en “neen” te wisselen. Dus het agens-in-context kan veronderstellen dat er een aantal veranderingen moet zijn die het kan waarnemen en dat dit begrensd kan zijn naar boven. Dat maximum neemt het agens dan als het maximum aantal stappen dat te tellen is. Vanuit de mogelijkheid tot tellen moet wel volgen dat we impliciet en onvermijdelijk veronderstellen dat de stappen even groot moeten zijn: de variabele n moet een minimaal en identiek verschil hebben. Dus n neemt toe vanaf een vrij gekozen 0 met gehele stappen (dus n=0, n=1, n=2, enz…) en neemt nooit af, n is een intensiteit en heeft dus een dimensie.

De inherente beperking tussen twee waarden (de waarden “ja” versus “neen”) wordt voor getallen perfect gemodelleerd door een sinus of een cosinus van een getal. De functies sinus of cosinus kunnen als input gelijk welk reëel getal nemen en het resultaat wordt in absolute waarde door het getal 1 beperkt omdat die goniometrische functies gedefinieerd zijn als een verhouding van twee getallen waarvan het grootste getal als invariante referentie (bijvoorbeeld 1) genomen wordt. Hieronder een voorbeeld van de cosinus van 32 stappen, met elke stap even groot.

In de hier volgende tabel geven we de getallen die in de grafiek voorgesteld worden.

Merk op dat geen enkele cosinus in absolute waarde groter wordt dan 1 en dat 1 nooit bereikt wordt behalve bij de start die we een nul kunnen toekennen. Gegeven de schaal van de grafiek is dat enkel waarneembaar in de tabel, onvermijdelijk beperkt tot 15 betekende cijfers. “Plus 1” of “min 1” wordt enkel bereikt bij het getal π en bij een geheel veelvoud van het getal π. Als elke stap overeenkomt met, ofwel +1 (of “ja”), ofwel -1 (of “neen”), dan kunnen we dat simuleren door eerst de geordende intensiteit van elke stap met een factor π te vermenigvuldigen en daarvan een goniometrische functie te nemen. De factor π heeft geen dimensie, het is een getal waarmee we de intensiteit n wijzigen zonder de entiteit “stap” (de dimensie van n) zelf te wijzigen. Dus in plaats van n=0, n=1, n=2, enz… te nemen, nemen we n=0π, n=1π, n=2π , enz…. De (co)sinus met de factor π brengt het modulair rekenen (minimaal een modulo 2) binnen om invariantie en verandering in de werkelijkheid voor te stellen en tezelfdertijd drukt de factor π uit dat de eenheid niet te kiezen is (π is niet commensurabel met een te kiezen eenheid). Daardoor maakt de factor π ook de geometrische interpretatie mogelijk. Bijvoorbeeld: de cosinus van een hoek in een rechthoekige driehoek is de verhouding van de aanliggende zijde tot de incommensurabele schuine zijde. Door voor π te kiezen drukken we de intensiteit van n uit in het geometrisch begrip “radiaal” (de eenheid van hoek: 1 radiaal is gedefinieerd als de grootte van de middelpunthoek van een cirkel waarvan de lengte van de boog gelijk is aan de lengte van de straal (de radius)). Dit maakt onmiddellijk duidelijk wat de veronderstelling is van de geometrische interpretatie: een cirkelboog, een lijn gekromd in twee dimensies dus waarvan de lengte niet te meten is, enkel te berekenen. Dit kunnen we contrasteren met de verhouding van de twee lijnstukken die een rechte hoek maken en die wel te meten zijn en ons een tangens leveren die niet in waarde beperkt wordt.

De getalwaarde van n is door deze gekozen factor gewijzigd naar een niet meer te kiezen getal. De hoek is dan 0 in het geval dat de intensiteit n even is, en π in het geval dat de intensiteit n oneven is. Een fractie van π is dan een hoek tussen 0 en π, en de hoek is modulo 2π. Dus: op een praktische manier tellen we geordend door gebruik te maken van de gehele getallen en afwisselend bekomen we een even en een oneven getal. We berekenen dan een cosinus gelijk aan +1 gevolgd door een cosinus gelijk aan -1 en dan weer een cosinus gelijk aan +1. De hoek is ook de meetwaarde van een rotatie en een rotatie is in het haakformalisme geen geometrisch begrip, de rotatie wordt gemodelleerd door een laatst toegevoegde onderscheiding (die altijd dezelfde waarde heeft en daardoor associativiteit mogelijk maakt). Ook de “laatst toegevoegde onderscheiding” is een zeer abstract begrip dat op verschillende manieren concreet kan gewaardeerd worden.

We kunnen er altijd van uitgaan dat het aantal toestanden dat E onvermijdelijk onderscheidt verschillend is van het aantal toestanden dat het waarnemend agens A onderscheidt, agens dat E waarneemt. Dit uit zich in het a priori onbekende aantal stappen die beide doorlopen als ze gedrag waarnemen. Toch kunnen beide tot dezelfde hypothese komen over het waargenomen gedrag als ze simultaan “ja” kunnen zeggen. We zullen interpreteren dat ze hiermee de schalen van hun stappen met elkaar coördineren. We hebben dat nu op een “agens-centrische manier” uitgedrukt maar we zullen gecoördineerd gedrag van deelentiteiten altijd waarnemen als een gedrag van een entiteit E-met-deelentiteiten. We kunnen vaststellen dat bijvoorbeeld twee entiteiten e₁ en e₂ die elkaar uitsluiten hetzelfde gedrag vertonen. We stellen dan vast dat <<<x₁>x₂><<x₂>x₃>...<<x_i>x_i+1>...<<x_n>e₁> en <<<x₁>x₂><<x₂>x₃>...<<x_i>x_i+1>...<<x_n>e₂>. Ze maken dus deel uit van dezelfde entiteit E die we dan als de disjunctie e₁e₂ begrijpen.

Daarom is de interpretatie van die hoek de (on)zekerheid (de waarschijnlijkheid tussen 0 en 1) van waarnemen van een gedrag, de verandering van een bepaald gekozen aspect. Inderdaad: maximale zekerheid (bijvoorbeeld “ja”) is er bij de hoek 0 en met de cosinus modelleren we “dat gedrag” als +1. Met de sinus modelleren we “iets anders dan dat gedrag”, met andere woorden: gedrag dat daar orthogonaal mee is. Dit is niet anders dan de M en M^<> die we gebruikten om de waarnemingscontext te definiëren, waarnemingscontext die voorgesteld wordt als de disjunctie MM^<> in het grootste universum. Ook hier zien we dat de hoek dus inherent tweedimensionaal is. In onze modellering van n als stappen in een proces van waarnemen komt dat overeen met de inherente onzekerheid over wat er gebeurt “tussen” twee waarnemingen die met zekerheid elkaar uitsluiten en dus komt dit ook overeen met een onzekerheid “tussen” twee sporen-met-zekerheid van een gebeurtenis. De hypothese van continuïteit is de uitdrukking van die onzekerheid: “indien we tussen stap n en stap n+1 zouden hebben kunnen waarnemen dan zouden we…”. De (on)zekerheid bij de hoek π/2 met een cosinus gelijk aan 0 drukt dan uit dat “niets” niet anders is dan “ongekend klein en onwaarneembaar kleiner”. De (on)zekerheid bij de hoek 0 (“ongekend klein en onwaarneembaar kleiner”) met een cosinus gelijk aan +1 drukt dan uit dat “ja” kan gebruikt worden om de ordening van de schalen waarop waargenomen wordt te normaliseren. Is de cosinus +1 dan is de sinus 0. Maximale zekerheid voor M is maximale zekerheid voor M^<> en vice versa.

Dit maakt van “een trilling” dus een concept dat coördinatie kan uitdrukken tussen toestanden: de (on)zekerheid van het waarnemen van de toestand (“de hoek”) kan even groot zijn, in welk universum de toestanden ook zouden uitgedrukt zijn, hoe ver ze ook van elkaar verwijderd zouden zijn: het is hetzelfde patroon.

Dit maakt van trilling dus een informatie concept hoewel het historisch niet zo ontstaan is.

We kunnen nu een grafiek maken met op de abscis de intensiteit n (gewogen met π) en op de ordinaat de waarde van de goniometrische functie (namelijk de intensiteit cos(πn)). Dit interpreteren we dan als de intensiteit op een nog naamloze dimensie orthogonaal met de entiteit “stap” (die als intensiteit n heeft en door de verschaling met π het karakter van een hoek gekregen heeft waarmee dan de mogelijkheid van simultane coördinatie beschikbaar wordt). Die beide dimensies hebben de naam “trilling” gekregen en de intensiteit is dus de amplitude van de trilling. De amplitude maakt het mogelijk om uit te drukken dat sommige sporen door sommige agentia-in-context al of niet kunnen onderscheiden worden. De amplitude kan “ongekend klein en onwaarneembaar kleiner” zijn voor een bepaald agens-in-context en de amplitude wordt in absolute waarde nooit groter dan 1, zoals bij een waarschijnlijkheid.

Het resultaat van de grafiek is dan “een golf die van -1 naar +1 springt en dit een aantal maal doet voor een aantal stappen”. Hieronder zien we een grafiek van de ordening van cos(0π) tot cos(32π), dus met n=32 stappen. De punten voor n komen overeen met maximale zekerheid, zo we willen +1 voor “ja”, -1 voor “neen”. De lijn tussen die punten is een hypothese (bijvoorbeeld: “indien we halverwege iets hadden kunnen waarnemen dan zou dat wel eens kunnen de intensiteit of amplitude nul geweest zijn”, maar die waarneming hebben we dus niet uitgevoerd omdat dit niet overeenkomt met een toestand die een andere uitsluit voor ons als agens-in-context dat onvermijdelijk in stappen waarneemt, de lijn die de punten in de grafiek verbindt is dus de uitdrukking van een hypothese.

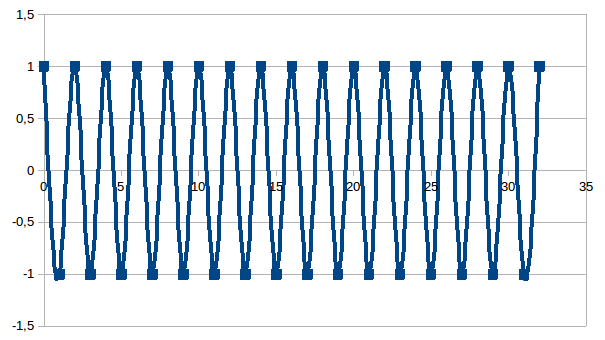
Een trilling en zijn mathematische voorstelling is dus een primitief meetinstrument voor elkaar uitsluitende stappen (of dat nu stappen zijn in de ruimte of in de tijd), dus een meetinstrument voor een totale ordening gerelateerd met de mogelijkheden van een agens-in-context. We hebben hiermee de onvermijdelijke grens van waarnemen gemodelleerd, namelijk: waarnemen is onvermijdelijk en doet zich aan het agens-in-context voor als stappen die elkaar uitsluiten en die z(h)ij niet kan kiezen. We kunnen niet weten of de stappen “even groot” zijn, maar we kunnen de stappen (achteraf) zeker tellen gebruikmakend van de gehele getallen en dan veronderstellen we impliciet dat ze “even groot” zijn. Dan zijn de stappen afwisselend door oneven en even getallen voorgesteld en de goniometrische functie zorgt er voor dat we kunnen uitdrukken dat ze niet te kiezen zijn. Anders geformuleerd: elk agens-in-context telt stappen in het grootste universum en die zijn voor het agens onvermijdelijk “even groot”, het verschil namelijk tussen “ja” en “neen”, de maximale simultaneïteitsafstand (de afstand tussen een focus en zijn inbedding, een aspect en zijn “anders”, een welgevormde haakuitdrukking en zijn inbedding) in het grootste universum dan kan opgespannen worden door het agens-in-context dat een gedrag waarneemt.

Golf als patroon genereert een golflengte

Op de n as kunnen we een verschil tussen elkaar uitsluitende stappen (dus toestanden) aflezen. Als verschil heeft het alle karakteristieken van een simultaneïteitsinterval met punten die elkaar uitsluiten. Hierbij kan een referentiepunt vrij gekozen worden (een verschil is altijd onafhankelijk van een referentiepunt). Elk verschil kunnen we dus zien als de intensiteit van een eenheid die invariant is voor een bepaalde keuze. Deze invariante wordt de golflengte genoemd. De golflengte G heeft een dimensie afgeleid van de dimensie van n (“stap”), namelijk een “verschil van stappen”, en is dus een entiteit. Door de keuze van de factor π wordt de golflengte dan gemeten in de eenheid van hoek (de radiaal), dus als verschil van hoeken, een “fase”. Elke stap genereert een hoek. Als we dan toch voor begrippen kiezen die een geometrische connotatie hebben, is een hoek nuttiger dan een afstand. Een golflengte is niet een verschil van afstanden maar een verschil van hoeken en een hoek is gedefinieerd modulo 2π. Die hoek kan voor elke stap dezelfde zijn, die hoek kan voor elke stap verschillen. Hoeken zijn verhoudingen van twee getallen en als zodanig modelleren ze een schaal. De golflengte modelleert dus een schaalverschil. Schaalverschillen kunnen we gebruiken om waarnemingen te coördineren (“in welk universum ze ook zouden uitgedrukt zijn, hoe ver ze ook van elkaar verwijderd zouden zijn”). Doordat een agens-in-context onvermijdelijk toestanden waarneemt, onvermijdelijk een hoek waarneemt als (onzekere) toestand, ontstaat daarbij onvermijdelijk een zeker verschil tussen twee stappen, een zekere golflengte en een golflengte kan bij elke stap veranderen. De golflengte is te gebruiken als alternatieve maat voor een aantal stappen, en als verschil is de golflengte onafhankelijk van een referentiepunt.

Het woord “golflengte” is historisch gegroeid. Golflengte ontstond bij het beschrijven van fysische (ruimtelijke) periodieke (tijd) verschijnselen zoals periodieke verschijnselen in een medium, verschijnselen die al snel gerelateerd konden worden aan de rotatie van een object rond een eigen as of rond een ander object. Historisch gezien wilden we een verschijnsel in de ruimte-tijd beschrijven, bij uitstek gerelateerd aan voortplanting van een patroon (dat is een proces) en de voortplantingssnelheid (processnelheid) van een patroon (bijvoorbeeld een geluid, een temperatuur enz…). We stellen ons een golflengte bijvoorbeeld voor als de lengte van de fysische afstand tussen twee golftoppen in een waterpoel, maar dit is maar één van de mogelijke interpretaties van de geïdealiseerde mathematische voorstelling als evoluerende hoogte van een plaats op het wateroppervlak. De connotatie hiermee kan het begrip ongewild een minder abstracte betekenis geven. Eigen aan periodiciteit en herhaalbaarheid is dat dit een uiting is van “een evenwicht”, van een aspect dat invariant is zodanig dat we sommige situaties, die niet bij elke waarneming waargenomen zijn, met zekerheid kunnen herkennen en anticiperen. Bijvoorbeeld: het wateroppervlak golft rond een evenwicht, deeltjes water roteren gecoördineerd zolang er genoeg energie aangevoerd wordt. Bijvoorbeeld: sta recht, kijk, draai rond je as en pas na een volle omwenteling zie je wat je eerst zag. Het gedrag van “wat je eerst zag” en wat je na de rotatie herkent als “datgene wat je eerst zag” kan enkel maar een hypothese zijn, het gedrag is immers niet waargenomen en leidt dus tot een “waarschijnlijk gedrag”. Indien je sneller op je as had kunnen draaien dan zou je meer “tussenliggende” aspecten van het gedrag hebben kunnen waarnemen. En het waarnemen van een opkomende en ondergaande zon kunnen we begrijpen met de hypothese dat de aarde om een as draait en dus de positie van sterren aan de hemel in de loop van de dag verandert, behalve op die positie die toevallig in het verlengde van de as ligt (in het noordelijk halfrond vinden we op die positie de Poolster). De toestanden (die de beweging van de zon modelleren en die we afleiden uit sporen die nagelaten worden) nemen we waar, de rest is onzeker. We hebben echter veel vertrouwen in de hypothese omdat ze ons in staat stelt met zekerheid de efemeriden voor een lange tijd op te stellen met een grote precisie die voldoende is voor praktische toepassing. De hypothese heeft echter zijn grenzen. Toen Henri Poincaré in de negentiende eeuw probeerde de algemene bewegingsvergelijkingen op te lossen van drie lichamen die elkaar aantrekken en ten opzichte van elkaar roteren, stuitte hij op inherente onvoorspelbaarheid: enkel als één van de massa’s veel groter is dan de andere kon hij paden ontdekken die kunnen geanticipeerd worden. Dit verklaart dan op zijn beurt de stabiliteit in ons gedeelte van de melkweg: roterende massa’s met voldoende grote verschillen in de grootte van de massa’s.

Al deze geometrische toepassingen van het begrip “golf” kunnen het abstract begrijpen ervan in de weg staan. Een golf is abstracter dan zijn ruimte-tijd toepassingen. Het is de herhaalbaarheid, de terugkeer van hetzelfde, de periodiciteit van de waarneming die onvermijdelijk in stappen verloopt, de modulariteit, de coördinatie tussen toestanden, die het mogelijk maakt om van een fase te spreken: twee golven kunnen exact hetzelfde patroon hebben maar ten opzichte van elkaar over een fase (een fractie van de golflengte) verschoven zijn, een verschil (van hoeken) kan dezelfde zijn ondanks het feit dat ze ten opzichte van een andere referentie gemeten zijn, (p-q) is niet anders dan ((p-0)-(q-0)), is niet anders dan ((p-r)-(q-r)). De fase is niet anders dan een hoek en elke hoek kwantificeert een waargenomen toestand in twee categorieën. Modelleert de ene golf de variatie waargenomen door agens 1, dan modelleert de tweede golf de variatie waargenomen door agens 2 en beide agentia delen niet dezelfde toestand, simultane waarneming is niet mogelijk en toch nemen beide hetzelfde patroon waar en kunnen ze dat gebruiken om ook hun ander gedrag te coördineren. Een golflengte geeft ons dus ook de mogelijkheid om verschillende autonome golven ten opzichte van elkaar te positioneren en dit te beschrijven door een getal, een verschil dus van een verschil van twee hoeken. Twee exact dezelfde golven (ze hebben dezelfde schaal, dus hetzelfde verschil van hoeken, dus hetzelfde patroon, dus dezelfde golflengte) kunnen ten opzichte van elkaar verschoven zijn in een eenheid die te meten is als een fractie van een golflengte, als een fractie van een aantal stappen. Als ze zouden verschoven zijn over exact een golflengte of een veelvoud daarvan dan zouden beide golven niet te onderscheiden zijn. De toestanden zouden simultaan zijn voor beide agentia (“hoe ver de toestanden zich ook zouden bevinden van elkaar”). De som van de intensiteiten (amplitudes) van zo’n twee onafhankelijke golven zou verdubbeld zijn en zo zouden we tot de conclusie kunnen komen dat er twee golven moeten zijn die interfereren en dit geeft betekenis aan de intensiteit “twee”. Als ze zouden verschoven zijn over exact een halve golflengte of een veelvoud daarvan dan zouden beide golven in tegenfase zijn en de som van hun intensiteiten zou nul zijn en zo ook zouden we tot de conclusie kunnen komen dat er twee golven zijn die interfereren en dit geeft betekenis aan de intensiteit “nul”. Dit geeft de mogelijkheid de amplitude van een trilling te interpreteren als de superpositie van trillingen met niet alleen eenzelfde patroon, maar die daarenboven ook in fase zijn. Dit is een onvermijdelijke hypothese: we moeten veronderstellen dat er meerdere onafhankelijke trillingen zijn als we een (variërende) amplitude waarnemen. De toestandsruimte wordt dan beschreven door toestanden waarin trillingen simultaan zijn.

Een verschil van twee hoeken kunnen we als eerste generatie van een verschil van toestanden interpreteren als een abstracte snelheid. Deze snelheid is constant als alle verschillen even groot zijn, en zoals we hoger motiveerden: als we tellen gaan we impliciet uit van even grote verschillen. Een schaalverschil is dan een abstracte snelheid en is dus een golflengte en een constante golflengte is een constante snelheid. Een verschil van een verschil van twee hoeken is dan een tweede generatie van een verschil van toestanden en dit kunnen we interpreteren als een abstracte versnelling. De verandering van golflengte is dus te interpreteren als een versnelling en te meten als een fase, een fractie van een aantal stappen. Golven in interactie herkennen we doordat het resulterend gedrag afhankelijk wordt van individuele golflengtes en dus fasen.

Hieronder een voorbeeld waarbij de golf met vierkante datapunten en de golf met ruit datapunten een fractie van een golflengte ten opzichte van elkaar verschoven zijn. Beide golven worden door dezelfde golflengte gekarakteriseerd, maar zijn dus niet “in fase”. De golflengte is niet de minimale golflengte en wordt dus beschreven met behulp van een factor van π groter dan 1. De golf met vierkante datapunten wordt beschreven door cosnπ(1,666666666666667), de golf met ruiten datapunten wordt beschreven door cosnπ(0,2+1,666666666666667). De fase is 0,2 en de schaal herkennen we in de factor 1,666666666666667 met de resolutie van onze berekening. De cosinus van π/3 is ½ en 1,666666666666667 herkennen we als 1+0,666666666666667=1+2/3=5/3=10/6=1/0,6.

Beide golven hebben dezelfde golflengte: 6 stappen (zoveel stappen zijn er tussen 0 en 2π: 0+π/3; π/3+π/3; 2π/3+π/3; 3π/3+π/3; 4π/3+π/3; 5π/3+π/3) en er zijn 5 volledige golven afgebeeld (functie van het a priori onbeperkt aantal stappen) en ze verschillen enkel door hun fase. De fase beschrijft dus iets dat een invloed zal hebben op de manier hoe we individuele golven (individuele waarnemingen) zullen kunnen sommeren om een intensiteit te beschrijven.

Interactie van trillingen is de modellering van de onvermijdelijkheid van waarnemen, een uiterste afwisseling van “ja” en “neen” overeenkomstig de uiterste onmogelijkheid van simultaneïteit, een situatie die niet te kiezen is. De as “stappen” is niet a priori beperkt en heeft een richting en twee zinnen, het is een praktische beperking omdat we wel moeten vaststellen dat entiteiten en hun waarnemingen komen en gaan en dit is energetisch te modelleren. De as hier loodrecht op is de as van de intensiteit van trilling. Intensiteiten kunnen we beschrijven door een aantal waarbij we individuele golven (abstracte constructies, los van tijd en ruimte) als eenheid veronderstellen (het zijn de “stappen” en dus “onze beperkingen of mogelijkheden”). Sommen en verschillen van onafhankelijke golven (die dus simultaan aanwezig kunnen zijn) geven ons de intensiteit van een trilling.

Hieronder de grafiek van de som van beide afgebeelde golven. De intensiteit is bijna een verdubbeling omdat beide golven bijna perfect in fase zijn.

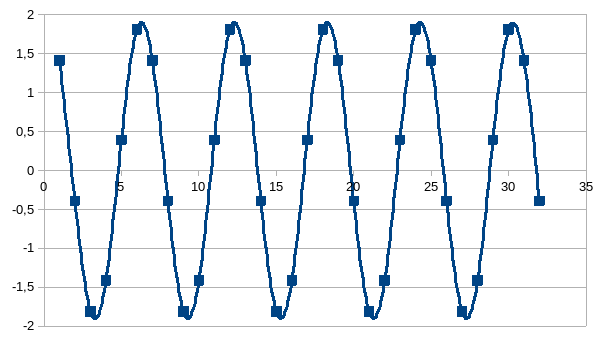
De intensiteit van de golflengte is de “afstand” (abstracte metrische maat) tussen twee opeenvolgende toestanden met maximale zekerheid: cos(0) en cos(2π) of cos(π/2) en cos(3π/2) en dit is niet anders dan 2 radialen, de omtrek van een cirkel met straal 1, dus “de afstand die overeenkomt met de hoek 2π” of 6,28318530717959 lineaire eenheden. De lineaire eenheden zijn een (fractie van de) golflengte en zijn hier uitgedrukt met 15 cijfers, de beperking van de hardware en software die gebruikt wordt om fracties te berekenen. Om de intensiteit van golflengte te kennen moeten we dus de intensiteit van één stap met een factor (in het voorbeeld is dit het getal 1+2/3=1,666666666666667) van π vermenigvuldigen en dit geeft dan de schaal van de grafiek op de n-as. In dit voorbeeld is er dezelfde maximale zekerheid slechts na 6 stappen (de golflengte, metrische maat voor de simultaneïteitsafstand). De totale afstand bij stap 32 is dan 32π(1+2/3) of dus 167,551608191456 uitgedrukt met 15 cijfers met een lineaire dimensie van n en dus kleinste intensiteit van een stap 0,00000000000001 die praktisch te kiezen is.

Hoeken en dus ook golflengten zijn modulo 2π gedefinieerd. Voor hoeken lijkt dat aanvaardbaar, ze worden voorgesteld als delen van een eenheidscirkel en deze figuur is deel van de opleiding die gegeven wordt als men met goniometrie begint. We stellen ons dat voor als een rotatie van een object rond een as. Maar ook golflengten zijn modulo 2π gedefinieerd, en als we ons dat willen voorstellen worden we gehinderd door de connotaties van de historische ontwikkeling van het begrip. We hebben begrepen dat we een golflengte in een lineaire maat kunnen uitdrukken en we stellen ons dat voor als de ruimtelijke afstand tussen twee golftoppen. Immers: om de intensiteit van golflengte te kennen moeten we de intensiteit van één stap met een factor (in het voorbeeld is dit het getal 1+2/3=1,666666666666667) van π vermenigvuldigen en dit geeft dan de schaal van de grafiek op de n-as. Maar er is natuurlijk helemaal geen verschil als we bij dat getal nu een even geheel getal tellen resulterend in 3+2/3=3,666666666666667, 5+2/3=5,666666666666667, enz… Dus cosπ(1+2/3)=cosπ(3+2/3)=cosπ(5+2/3)=cosπ(2m+1+2/3). Deze schalen zijn even valide golflengten en er is geen enkele schaal a priori gegeven, we moeten ze allemaal kunnen veronderstellen. We worden nu gehinderd door onze ruimte-tijd a priori en verbinden hoek en golflengte met een tijd-afstand of een ruimte-afstand maar dit zijn maar interpretaties om ons iets voor te stellen, dus op een schaal die voor ons waarneembaar is. Een “trilling van onzekerheid” is geen ruimte-tijd fenomeen. Dit is helemaal niet verwaarloosbaar want we hebben wel moeten ontdekken dat we omgeven worden door een praktisch ontelbaar aantal entiteiten die kunnen interageren en zo een zeker gedrag zullen vertonen. Om hun gedrag te modelleren hebben we dus grote getallen nodig, en dat terwijl de beperkingen van onze machine en zijn software een limiet van berekenbaarheid opleggen (zelfs als we die limiet zo klein kunnen kiezen als we zouden willen). Als we in ruimte-afstand willen blijven denken, dan is de kleinste afstand die op dit moment praktisch waarneembaar is ongeveer 10^-15 meter (de grootte orde van de diameter van een atoomkern). In vergelijking hiermee: het aantal atomen in een effectief te wegen hoeveelheid zuivere materie (dus met de dimensie “per mol”) is de constante van Avogadro, een intensiteit van de grootteorde van 10²³. We kunnen dus verwachten dat de simultane trilling van 10²³ atomen zal leiden tot niet te verwaarlozen interferentie op verschillende schalen (en dus verschillende golflengten) die als een intensiteit op die schaal meetbaar zijn, intensiteit die enkel het resultaat is van collectief gedrag. Superpositie van twee golven leidt immers tot een emergent verschijnsel: een nieuwe verhouding die “de groepsnelheid” genoemd wordt, een verschijnsel met een golflengte die anders is dan de golflengte van de constituerende golven. We verwachten dus dat we dat met onze machine-context gebonden resolutie sommige superposities van golven niet kunnen simuleren en als we de resolutie opdrijven zullen we altijd nieuwe verschijnselen gaan waarnemen.

Patronen van onzekerheid

We zien dus in het voorbeeld dat we met golven in staat zijn gedrag te modelleren met een variatie die anders is op andere schalen (andere factoren van π, andere golflengtes). Dit willen we nu precies beschrijven door de effecten van de schaalfactor uit het voorbeeld in hun algemeenheid te onderzoeken.

De dimensie van n (“stap”) kunnen we verschillende namen geven. Door de keuze voor π kunnen we de dimensie een “hoek” noemen, tweedimensionaal, maar de dimensie kan in sommige toepassingen natuurlijk eendimensionaal zijn zoals seconde of meter, de dimensies die we gebruiken om (elkaar uitsluitende) fysische sporen van een laatst toegevoegde onderscheiding mee aan te duiden. In het eerste geval zeggen we dat de golflengte gelijk is aan 6,28318530717959 seconde, in het tweede geval dat de golflengte gelijk is aan 6,28318530717959 meter. Hiermee geven we de n as een dimensie en een lineaire schaal die praktische interpretaties zijn van “een stap” van toestand naar toestand. De hypothese van de speciale relativiteit is trouwens dat meter en seconde in elkaar om te zetten zijn met een factor c, en we kunnen aantonen dat elke verhouding inherent begrenst zal zijn. Het inzicht dat we een fractie van π slechts met een aantal betekende cijfers kunnen weergeven hoeft ons nu niet meer te verontrusten maar kan ons aanzetten tot verder onderzoek.

De interpretatie die we willen beklemtonen voor de grafiek voor een trilling tussen +1 en -1 is dat dit het patroon uitdrukt dat er om de 2 onvermijdelijke stappen (want iets sluit iets anders onvermijdelijk uit voor een agens-in-context) maximale zekerheid is dat het waarnemend agens een spoor waarneemt dat als “ja” kan genoteerd worden (en de duale interpretatie is natuurlijk dat er om de 2 stappen maximale zekerheid is dat het waarnemend agens een spoor waarneemt dat als “neen” kan genoteerd worden). Om de stap is er dan maximale zekerheid, afwisselend “ja” en “neen”. Dat is het invariante aspect, in het model is dit het ervaren punt MM^<> dat de aanwezigheid “ja” vertoont en het gedrag “ja of neen” vertoont. Voor de aanwezigheid “ja” is het gedrag “ja of neen” een disjunctie, geen exclusieve disjunctie. Het gedrag is irrelevant voor de aanwezigheid, maar wordt blijkbaar altijd ervaren (en kan dus gemodelleerd en zelfs gekwantificeerd worden) als een mate van zekerheid tussen 0 en 1. Het meest “gedetailleerde” niveau van beschrijven (met een laatst toegevoegde onderscheiding) kan blijkbaar enkel een waarschijnlijkheid zijn. De golflengte is de metrische afstand tussen twee elkaar uitsluitende punten: de disjunctie (!) M_iM_i^<> (met i=2) “van maximale zekerheid” “ja of neen” met “ja of neen” een disjunctie, geen exclusieve disjunctie meer (het doet er niet toe of er nu “ja” of “neen” toegekend werd, immers: alle M_iM_i^<> hebben dezelfde waarde). Een referentiepunt kan vrij gekozen worden en wat er dan gebeurt moet blijken te gebeuren. Die afstand verandert niet wanneer hetzelfde getal bij de beide punten opgeteld wordt of wanneer hetzelfde getal van de beide punten afgetrokken wordt en die afstand heeft dus het patroon van een verschil tussen toestanden. Een verschil kent altijd twee elementen. We herkennen dat ook als een eigenschap van “processnelheid”. Dit alles komt perfect overeen met de maximale metrische afstand tussen <<>> en <> (of a en <a>). De kleinste hoek is dan niet anders dan de simultaneïteitsafstand tussen twee punten die elkaars buur zijn. Hoe groter het onderscheidingen universum hoe kleiner de hoek kan zijn, hoe meer stappen kunnen onderscheiden worden tussen “ja” en “neen”. Het pad is dan niet anders dan het pad in een simultaneïteitsinterval tussen twee punten met maximale zekerheid. Zoals we begrepen hebben met het structuurgetal “hoek” kunnen we ons dat voorstellen als het pad dat gevolgd wordt tussen een extremum (bijvoorbeeld <<>>) met n bits-met-dezelfde-waarde en een fijner punt met (n-m) bits-met-dezelfde-waarde, waarbij de afstand gemodelleerd wordt door het aantal toestanden p en n-m-p die in twee categorieën onderverdeeld zijn, dus twee elkaar uitsluitende punten die het fijner punt met n-m bits-met-dezelfde-waarde realiseren, een categorie “ja” en een categorie “neen”. De laatst toegevoegde onderscheiding heeft dus een waarde <<>> als we dat als extremum kiezen. We kunnen ons dan voorstellen dat de intensiteit van <<>> stap voor stap toeneemt van 0 tot +p, vervolgens van +p tot 0, vervolgens van 0 tot -p, vervolgens van -p tot 0 (of volledig duaal van 0 tot -p, vervolgens van -p tot 0, vervolgens van 0 tot +p, vervolgens van +p tot 0). In de tweede categorie gaat de intensiteit dan van (n-m)-p tot (n-m)+0, vervolgens van (n-m)+0 tot (n-m)+p, vervolgens van (n-m)+p tot (n-m)+0. Bij elke stap is de som van de intensiteiten in de categorieën gelijk aan n-m en dit proces is minimaal in twee dimensies te beschrijven, de dimensie M en de dimensie M^<>. De grootte van elke stap is vrij te kiezen maar is beperkt door n, het totaal aantal te onderscheiden toestanden in het grootste universum dat een agens-in-context kan opspannen. De vrije keuze kan enkel een vrije keuze van een schaal zijn (een factor voor de abscis) waarop de waarnemingen beschreven worden. Dus: “ja, dit ervaar ik” is een vrije keuze en legt een schaal vast waarop het gedrag kan beschreven worden van datgene dat invariant in het ervaren is.

Invariantie modelleren we dus als een modulair aspect en dat is ook te herkennen in het voorbeeld van een fysische rotatie van een object rond een eigen as of rond een ander object wat de geometrische interpretatie mogelijk maakt. Wat die stappen zijn wordt uitsluitend bepaald door de beperkingen van de waarneming die zich uit in de onmogelijkheid van het simultaan zijn van twee waarnemingen (en die dus elkaar uitsluiten, die dus toestanden zijn). Elk agens wordt beperkt door de beperking van elkaar uitsluitende stappen. Dit kunnen we vanaf nu dus ook uitdrukken door een hoek (een verhouding als een processnelheid), een golflengte (een verschil van hoek). Dit demonstreren we helder in onderstaande grafiek: voor de datapunten met vierkant is er maximale zekerheid om de 2 stappen, voor de datapunten met ruit is er maximale zekerheid om de 16 stappen maar ook zijn er tussenliggende min-of-meer-zekere punten, punten met een waarschijnlijkheid van waarnemen tussen 0 en 1. Die punten zou het agens onderscheiden indien het in staat zou zijn om het proces dat de datapunten met vierkant genereert op te nemen in de meetcontext voor het proces dat de datapunten met ruit genereert. Dat is op zijn beurt niet meer en niet minder dan simultaneïteit. Dit moeten we in twee uitspraken uitdrukken waarbij de waarschijnlijkheid heel duidelijk naar voor komt. Enerzijds: een tralie die door 2ⁿ toestanden opgespannen wordt, heeft met zekerheid ook een (deel)tralie die door 2^n-1 elkaar uitsluitende punten opgespannen wordt. Anderzijds: een tralie die door 2ⁿ toestanden opgespannen wordt, is misschien ook een deeltralie van een tralie die door 2ⁿ⁺¹ elkaar uitsluitende punten opgespannen wordt. Merk het contrast op tussen zekerheid en waarschijnlijkheid die inherent verbonden zijn met het begrip “simultaneïteit”.

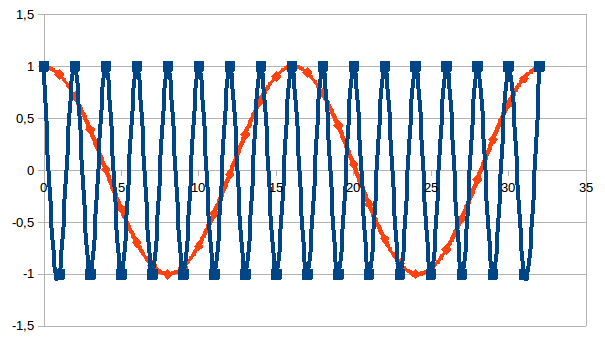
De grafiek maakt dus duidelijk dat we exact hetzelfde als volgt kunnen uitdrukken: slechts om de m aantal stappen is er dezelfde grootte van (on)zekerheid dat iets herkenbaar aanwezig is. Wat er tussen de stappen van maximale zekerheid gebeurt is onzeker en indien we die onzekerheid niet kunnen verdragen dan zoeken we een bevredigende hypothese die we proberen te kwantificeren zodanig dat het ook (door anderen of op andere standpunten) kan waargenomen worden. Dus het beeld van het “verbindend pad” in de toestandsruimte is een hypothese, is van de soort “indien we die stap hadden kunnen nemen, dan zouden we met zekerheid een bepaalde (on)zekerheid vinden”. De onvermijdelijke onzekerheid verontrust niemand die begrepen heeft dat de werkelijkheid die gedeeld wordt door verschillende agentia een potentiële constructie is die onze zekere ervaringen met elkaar kan verbinden. Inderdaad: agens A₁ (die, enkel voor zichzelf, om de twee stappen de zekerheid “ja” heeft) kan dezelfde werkelijkheid delen met agens A₂ (die, enkel voor zichzelf om de twee stappen dezelfde zekerheid “ja” vindt zoals ook agens A₁, maar een zekerheid die door agens A₁ beschreven wordt als dezelfde zekerheid om de 16 stappen van agens A₁, stappen die agens A₂ niet kan nemen). Ondanks de schaalverschillen kunnen ze die twee toestanden met zekerheid delen: ze zeggen simultaan “ja”. Het pad in een gemeenschappelijke toestandsruimte kan dus heel verschillend zijn voor verschillende agentia. Hierbij moeten we “agens” zeer ruim interpreteren: het is een veranderende entiteit (gedrag dus van een invariante entiteit) beschreven in een toestandsruimte. Een voorbeeld hiervan zijn drie massa’s die dank zij een gedeeld gravitatieveld met elkaar interageren. Toen Henri Poincaré de toestandsruimte onderzocht die hierdoor opgespannen wordt stuitte hij op de deterministische chaos (dit werd bekend als het drie- of meer lichamenprobleem). Sindsdien zijn er steeds meer voorbeelden beschikbaar geworden van systemen die geen uniek, met zekerheid voorspelbaar, pad doorlopen in een toestandsruimte (kent men het startpunt in een toestandsruimte, dan kan het volgende punt in de evolutie zich in een heel gebied van de toestandsruimte bevinden en is niet a priori gekend). De evolutie moet dan op andere manieren beschreven worden. Het model van een golf helpt ons om die onvermijdelijke waarschijnlijkheid te kwantificeren.

Een invariante waarneming hebben we een patroon genoemd. Het patroon is hier “om de m aantal stappen is er dezelfde grootte van (on)zekerheid dat iets herkenbaar aanwezig is”. Dit patroon is dus een golf, maar dan op een meer abstracte manier geformuleerd. Meer hebben we niet moeten veronderstellen dan het herhaaldelijk herkennen (“ja”) van een toestand door een agens-in-context, en dus impliciet een ordening. Er mag maar er moet niet “iets zijn dat golft”. Een golf beschrijft gedrag, verandering, proces van iets dat herhaaldelijk waargenomen wordt en de hypothese dat “iets” een gedrag vertoont is een constructie die uitgevoerd wordt door een agens-in-context als het in staat is binnen zijn beperkingen een keuze van “een invariante entiteit” MM^<> te maken. Het patroon van waarnemen is de basis en dan pas, met die basis worden hypothesen geformuleerd die dan de entiteiten zijn die op die manier kunnen waargenomen worden.

Die constructie is altijd mogelijk aangezien de ultieme disjunctie MM^<> gegeven wordt door het punt <>.

Maximale zekerheid en aanpassing van de waarnemingsresolutie

Door de introductie van “schaal van waarnemen” kunnen we nu de “indien…, dan…” hypothese voor golfverschijnselen verder onderzoeken.

Schaal en frequentie van zekerheid

De schaal herkennen we als een factor, noem deze f, die bepaald wordt door de verhouding van het aantal golven g tot het aantal stappen n. Dat is niet anders dan de verhouding van een aantal waarnemingen met maximale zekerheid tot een aantal stappen. De factor kunnen we, maar moeten we niet wegen met 2π, namelijk f=2πg/n is de factor die mathematisch perfect +1 en -1 kan bereiken en π kunnen we daarvoor gebruiken. De factor is dimensieloos, namelijk een verhouding van een “lokaal” verschil van stappen tot een “totaal” verschil van stappen. Met het voorbeeld: de datapunten met vierkant hebben een factor (2π)16/32 en dus π (en dat was ons uitgangspunt in de eerste grafiek die +1 en -1 kon bereiken, en drukken we op een lineaire manier onvermijdelijk met slechts een beperkt aantal betekende cijfers uit, namelijk 3,14159265358979), de datapunten met ruit hebben een factor (2π)2/32 of π/8=0,392738633480274 (eveneens met een beperkt aantal betekende cijfers). Dit inzicht geeft ons de mogelijkheid om nog een verhouding te construeren: de factor (dimensieloos) gedeeld door de golflengte (met de dimensie van n, namelijk “stap” of “verschil tussen twee toestanden”), dus in het geval van de vierkante datapunten is dit π gedeeld door 2π, in het geval van de ruiten datapunten is dit π/8 gedeeld door 2π. Die verhouding heeft de dimensie van 1/n (de reciproque van n) en is dus eveneens een entiteit, maar dan met de dimensie “reciproque stap” of “per stap”. De reciproque stap is een schaal waarbij het totaal verschil altijd groter is dan een deel van het verschil zoals bij de gewone stap (er geldt additiviteit), maar in tegenstelling met de gewone stap waarvan we kunnen veronderstellen dat elke stap gelijk is aan 1 (en dus even groot), is elke stap bij de reciproque stap ook even groot maar kleiner dan 1. Die verhouding 1/n wordt de frequentie F genoemd en is dus afhankelijk van n en n halen we uit de golflengte. Dus de frequentie is een maat voor het totaal (!) aantal toestanden die met zekerheid onderscheiden kunnen worden. De frequentie van de golf die we in de grafiek konden representeren met vierkante datapunten is dan π/2π=1/2. Inderdaad: bij stap 2 is er 1 golf doorlopen, en dus bij stap 1 een halve golf want 1/2+1/2=1. In het geval van de ruiten datapunten is dit 1/16, bij stap 16 is er 1 golf doorlopen, dus per stap wordt 0,0625 golf doorlopen want de som van 16 stappen 0,0625 is 1. Eens we een aantal stappen gekozen hebben kunnen we dus spreken van een frequentie van zekerheid, en in het gekozen voorbeeld is dit 0,5 “per stap” en 0,0625 “per stap” wanneer we n meten in “stappen”. De frequentie van zekerheid is de kwantificering van een maximaal aantal stappen dat onderscheiden kan worden. Wanneer we in de dimensie seconde meten dan is dit 0,5 respectievelijk 0,0625 per seconde, wanneer we in de dimensie meter meten dan is dit 0,5 respectievelijk 0,0625 per meter. Wat er dan (met zekerheid) aanwezig is hangt af van de waarneembare dimensie die invariant is maar een variant gedrag vertoont. Het is het gedrag van de entiteit die ontstaan is. Nemen we bijvoorbeeld mieren waar dan kunnen we uitdrukken dat we vaststellen dat er één mier per waarneming (per stap) waarneembaar is, of één mier per seconde, of één mier per meter, of één mier per volume (mieren hebben zelf een volume en kunnen niet hetzelfde volume innemen...) enz… Nemen we een bepaald gedrag van een mier waar (bijvoorbeeld een voelspriet naar de grond richten) dan kunnen we uitdrukken dat een mier dat gedrag om de p waarnemingen vertoont en verder onderzoek zou kunnen uitwijzen dat p een functie is van q enz…. Deze voorbeelden maken duidelijk dat het onderscheidend vermogen van de waarneming hierbij maatgevend is en dat er iets herhaaldelijk moet waargenomen worden. In de meetcontext zouden we dan processen met een hogere frequentie (neem de vierkante datapunten) kunnen gebruiken om de processen met een lagere frequentie (neem de ruit datapunten) van getallen te voorzien. Dit inzicht maakt ook duidelijk dat we het centraal axioma ook kunnen uitdrukken als volgt: een agens-in-context neemt altijd waar “met de hoogste frequentie van zekerheid” en dat is agens en context gebonden, onvermijdelijk en niet te kiezen. Het agens kan daardoor “met lagere frequenties van zekerheid” uitspraken doen over gebeurtenissen van een met zekerheid geanticipeerde waarschijnlijkheid. Aangezien dat geldt voor elk agens-in-context zal communicatie tussen agentia enkel mogelijk zijn op een lagere frequentie van zekerheid, en dat gezien vanuit het standpunt van elk communicerend agens-in-context. We kwantificeren hierbij de “indien…, dan…” constructie met behulp van een waarschijnlijkheid. Stel dat alle agentia-in-context een andere “hoogste frequentie van zekerheid” zouden kennen die a priori onbekend is, dan zouden hun waarnemingen toch kunnen overeenkomen (“resoneren”) op “lagere frequenties van zekerheid” en die resonantie zou met zekerheid waargenomen worden door elk agens-in-context. Dit betekent dat ze het eens zouden zijn over de (herhaaldelijk waarneembare) toestand die waargenomen wordt op een bepaalde stap die simultaan gezet wordt, maar voor het agens A₁ is dat bijvoorbeeld “zijn stap n₁” en voor het agens A₂ is dat bijvoorbeeld “zijn stap n₂”. Het ene agens zou bijvoorbeeld “direct” waarnemen, het andere zou voor de waarneming bijvoorbeeld een redenering (“indien… dan…” constructie) moeten opzetten. Als we twee gebeurtenissen (G₁ en G₂) veronderstellen waarover beide agentia het eens zijn dan is het perfect mogelijk dat G₁ direct waargenomen wordt door A₁ en geconstrueerd moet worden door A₂, terwijl G₂ direct waargenomen wordt door A₂ en geconstrueerd moet worden door A₁. Simultaneïteit betekent voor het ene agens iets anders dan voor het andere agens. Communicatie is slechts mogelijk op de laagste frequentie van zekerheid en zal dus zorgen voor frustratie bij elk agens.

Gebruik makend van een analogie met geluidsfrequenties zouden we kunnen zeggen dat de beide agentia op dezelfde grondtoon communiceren maar andere boventonen waarnemen. De boventonen zijn hogere frequenties die de noodzakelijk voorwaarde uitmaken voor waarneming op lagere frequenties. De grondtoon komt dan overeen met de frequentie van de laatst toegevoegde onderscheiding die in het ene geval in de tralie ingebouwd zit en waarvoor in het tweede geval een tralie moet opgebouwd worden. Een intensiteit is altijd een verhouding: een veelvoud van eenzelfde resolutie, dezelfde eenheid die een intervalmeting mogelijk maakt, namelijk het aantal atomen die elkaar uitsluiten (toestanden) en simultaan zijn zoals in een simultaneïteitsinterval. Dit is de eenheid van het maximale (minimale) verschil tussen toestanden. Er is inderdaad experimenteel vastgesteld dat, als het juiste patroon van boventonen aangeboden wordt, de mens de grondtoon spontaan construeert, zelfs al kan die frequentie niet fysisch aangetoond worden.

Patroon

In een voorbeeld hebben we gezien dat een golf met vierkanten datapunten en de golf met ruiten datapunten een fractie van een golflengte ten opzichte van elkaar kunnen verschoven zijn terwijl beide golven door dezelfde golflengte (verschil van stappen van zekerheid of verschil van frequentie van zekerheid) gekarakteriseerd worden. Dus dezelfde golf (hetzelfde patroon) kunnen we op een onbeperkt aantal andere manieren construeren door naast π ook een andere factor te gebruiken, stel f. “Naast π” betekent een fase, een hoek als som of verschil met π. Namelijk het patroon van cos(πn) kan ook geconstrueerd worden door cos(πn±fn)=cosπn(1±f/π) voor een factor f die verschillend kan zijn van π. Het patroon is de verandering van een hoek modulo 2π die gemodelleerd wordt door de cosinus.

Essentieel is nu het inzicht dat we wel een f kunnen kiezen maar dat we onmogelijk een f kunnen kiezen die gelijk is aan π. Immers: π heeft een onbeperkt aantal cijfers, wat we demonstreerden door het beperkt aantal betekende cijfers (die ons in de berekening op onze machine als enige precieze mogelijkheid aangeboden worden) expliciet te vermelden. Dus als we cos(πn±0) of cos(πn±fn) noteren is dat een illusie, een te mooie hypothese. We zouden beter het patroon als cos(f₁n±f₂n) noteren. We drukken hiermee uit dat we in praktijk de twee factoren (f₁ en f₂) kunnen kiezen en onvermijdelijk moeten kiezen en dat we één van beide als de best gekozen benadering van π beschouwen en dat is dan onvermijdelijk agens-in-context gebonden (bijvoorbeeld wij met onze machine en sofware). Hoe dan ook zijn cos(f₁n) en cos(f₁n±f₂n) goed gedefinieerd en hebben we het getal π helemaal niet nodig als we het getal 1 (en dus ook -1 en 0) voldoende dicht benaderen. We kunnen altijd schrijven: cos(fn)=1-k of cos(fn)=0+k met k willekeurig klein. De cosinus is onvermijdelijk een dubbelgetal waarvan we de onbekende term niet willen zien.

Dit betekent dat er voor elke keuze van een factor f een golflengte (schaalverschil) G zal kunnen berekend worden die een goede benadering is voor een gedrag dat wel kan gebeuren maar niet kan gekozen worden. Dat is juist wat we willen modelleren en waarvan we de gevolgen willen onderzoeken om de beperkingen van het model “golf” te leren kennen.

Een som en verschil van factoren

De factor f heeft beperkingen die gebonden zijn aan het aantal n. De kleinste golflengte (dit is het verschil tussen elkaar uitsluitende toestanden in de grootste toestandsruimte) wordt immers bepaald door de n waarbij cos(2πn)=1 en daaraan moeten de mogelijke sommen of verschillen van factoren ook voldoen. Neem nu twee factoren, stel f₁ en f₂, die π benaderen. Dit betekent dat we ze kunnen kiezen als alternatief voor π dat een getal is dat niet kan gekozen worden. Dus voor een som van die twee factoren, overeenkomstig cos(πn+πn)=cos(2πn)=1, moet gelden dat cosn(f₁+f₂)=1. En zo ook voor een verschil van die twee factoren, overeenkomstig cos(πn-πn)=cos(0)=1, moet gelden dat cosn(f₁-f₂)=1. Hiermee kunnen we dus uitdrukken “dat ze alternatieven zijn voor π”. Dus door de som van de twee te nemen, dus cosn(f₁+f₂)+cosn(f₁-f₂) wat niet anders is dan de superpositie van twee golven kunnen we 1 benaderen tot een gewenste of bereikbare nauwkeurigheid zonder daarvoor π nodig te hebben. Daarenboven zullen we onvermijdelijk meerdere golflengtes vinden omdat een goniometrische functie een modulo functie is (een periodieke functie). Een eerste soort mogelijkheden vinden we door te berekenen wat de gevolgen zijn van de gelijkheid voor een geheel aantal (±k) keren een som met 2π, een tweede soort mogelijkheden vinden we door te berekenen wat de gevolgen zijn van de gelijkheid voor het verschil met 2π van de mogelijkheden in het eerste geval. Merk op dat cosn(f₁+f₂)+cosn(f₁-f₂)=2cosnf₁cosnf₂. Dus f₁ kunnen we als geheel getal nemen en f₂ als een fractie van 1.

In de praktijk (dus door een rekenmachine te gebruiken voor onze berekeningen waardoor we uitdrukken dat wijzelf een agens-in-context zijn die zijn context expliciet benoemt) kunnen we dus nooit voor π kiezen. Het getal dat we als surrogaat voor π gebruiken heeft een beperkt aantal cijfers. Toch moeten we dat getal gebruiken om de cosinus te berekenen en dat getal is impliciet gekozen door een bepaalde rekenmachine te gebruiken. Dat is onze onvermijdelijke referentie, de onvermijdelijke factor die leidt tot een onvermijdelijk verschil tussen elkaar uitsluitende toestanden, namelijk een welbepaalde onvermijdelijke golflengte π die echter nooit kan gekozen worden. We kunnen deze redenering nu omkeren en een bepaalde golflengte (en dus een aantal stappen) kiezen en van daaruit een factor bepalen en dan kunnen we beide schalen met elkaar vergelijken. We kunnen dit als volgt modelleren: veronderstel 2n stappen en n is een geheel getal. We zorgen er nu voor dat er dan voor verschillende golven maximale zekerheid is, dat moet dus overeenkomen met een geheel aantal golven (gehele getallen zijn altijd te tellen). Dat aantal golven (en dus met een bepaalde golflengte) moet dus n zijn (n maal de intensiteit +1 en n maal de intensiteit -1). Dit betekent dat we stap 2n kunnen laten overeenkomen met n maal een bepaalde verhouding en die verhouding zal dus π benaderen met de beperkingen van de gebruikte resolutie van de simulatie. Het resultaat van dit inzicht is dat we dus cos(f₁n) berekenen met een factor f₁ en dat gebruiken als referentie. We geven hiervan een aantal voorbeelden:

Het aantal stappen dat twee opeenvolgende 2π benadert is niet anders dan de kleinste golflengte. In de tabel zijn dat van links naar rechts de golflengten 2, 4, 8, 16, 32 en 2π wordt bereikt voor respectievelijk 2f₁, 4f₁, 8f₁, 16f₁, 32f₁. Dat is niet anders dan (32/16)f₁, (32/8)f₁, (32/4)f₁, (32/2)f₁, (32/1)f₁. Dat zijn concrete invullingen voor (2n/g)f₁ waarbij f₁ de verschaling geeft van de n-as die resulteert in een aantal golven op die verschaling.

Een golf als hypothese

In plaats van een aantal stappen te tellen, tellen we nu een aantal golven. We zullen nu veronderstellen dat a een uiterste waarnemingsresolutie kwantificeert die a priori onbekend is en dat we een aantal stappen tellen en dat aantal beschouwen als een factor voor a. We zullen nu aantonen dat ook een aantal golven kan geteld worden en dat we dat als alternatief voor een aantal (geordende) stappen kunnen gebruiken waarmee we de ordening van de stappen een andere schaal geven. We modelleren dus dat sommige toestanden, waarvan de verschillen met een andere toestand enkel op de hoogste resolutie (namelijk a) kunnen onderscheiden worden, ook op een andere schaal kunnen onderscheiden worden. Maar op die andere schaal genereren ze dan andere verschillen met toestanden die ook op die schaal onderscheiden worden. Beide verschillen zijn te kwantificeren door een ander aantal golven dat kan geteld worden.

Om dit aan te tonen moeten we wel een keuze maken voor a en we stellen a=2^-nπ. Dit is een verhouding met een kiesbaar getal en een niet te kiezen getal. We stellen nu een tabel op met cos(mg2^-nπ) met m en g gehele getallen, m starten we bij nul en laten we per eenheid toenemen, g is een geheel getal dat gekozen wordt voor de hele tabel en geeft dus het aantal golven dat op 2π bereikt wordt met de meest onderscheidende resolutie 2^-nπ. Alle getallen zijn onvermijdelijk beperkt tot hetzelfde aantal na de komma, het resultaat van de beperkingen van de berekeningen. Diezelfde beperking geldt voor elk van de kolommen van de tabel die de resoluties tonen, resoluties die beschikbaar worden als inverse machten van 2, dus 2^-1, 2^-2, 2^-3, …, 2^-n. Dit betekent dat we in die kolommen een selectie maken van exact dezelfde getallen die ook in de hoogste resolutie 2^-nπ bereikt worden. Hiermee modelleren we dus dat, ondanks het feit dat alle getallen een onbeperkt aantal betekende cijfers hebben, sommige getallen in een aantal kolommen niet kunnen weergegeven worden omdat de verschillen met behulp van de resolutie in die kolom niet bereikbaar zijn. In deze voorstelling zien we dus een fractaal structuur gezien vanuit één niveau van elkaar uitsluitende punten, het niveau met het grootste onderscheidend vermogen, waarvoor dus het grootste aantal onderscheidingen moet gemaakt worden.

In de tabel geven we een voorbeeld voor n=5, g=21 m=64, dus 2π wordt bereikt op stap 64. Toch is stap 64 (als intensiteit van een stap) enkel meetbaar in de kolom met kop cosmgπ2^-(n-0), want de kolom met kop cosmgπ2^-(n-1) kent maar 32 stappen, de kolom met kop cosmgπ2^-(n-2) kent maar 16 stappen enz…. We kunnen dat ook als volgt uitdrukken: alhoewel wiskundig geldt dat het gemiddelde van m2^-n=0,0625 en m2^-n=0,125 gelijk is aan m2^-n=0,09375, toch is dat voor kolom met kop cosmgπ2^-(n-1) niet beschikbaar omdat dit een resolutie vereist die in 32 stappen niet beschikbaar is. Een gemiddelde nemen is slechts zinvol als je dat effectief kan uitvoeren. De veronderstelling dat men altijd een gemiddelde kan nemen is niet anders dan de veronderstelling van continuïteit en dat is een bijkomende hypothese, hypothese die niet te kiezen is en enkel kan blijken te gebeuren, hypothese bovenop de hypothese “golf”.

De grafiek die in elke kolom opgenomen is drukt het resultaat uit dat met die selectie van punten leidt tot een hypothetische golf (de verbindende lijn is voor elke grafiek een hypothese). De relatie met het aantal te onderscheiden stappen is duidelijk te zien. Het aantal punten is niet anders dan het aantal niveaus in een tralie met n onderscheidingen en we hebben aangetoond dat een niveauverschil een metrische maat is en een punt op een bepaald niveau zal een simultaan aspect modelleren.

We hebben zes golven voorgesteld. Alhoewel ze een andere golflengte hebben zijn er alle zes in fase en ze zullen resoneren met elkaar.

Het aantal golven op het niveau met de meeste onderscheidingen kunnen we vrij kiezen. Voor deze tabel hebben het totaal aantal golven (namelijk 21) zo gekozen dat het aantal golven het geheel gedeelte is van een derde van het aantal punten (3/3=1,0; 5/3=1,666666666666667; 9/3=3,0; 17/3=5,666666666666667; 33/3=11,0; 65/3=21,666666666666667). Hiermee willen we ook aantonen dat er nieuwe patronen kunnen ontstaan, bijvoorbeeld:

cosπ((0+1)/3)=½

cosπ((2¹+1)/3)=cosπ(3/3)=cosπ(0+1)=-1

cosπ((2²+1)/3)=cosπ(5/3)=cosπ(1+2/3)=cosπ(1,666666666666667)=½

cosπ((2³+1)/3)=cosπ(9/3)=cosπ(2+1)=-1

cosπ((2⁴+1)/3)=cosπ(17/3)=cosπ(5+2/3)=cosπ(5,666666666666667)=cosπ(1,666666666666667)=½

cosπ((2⁵+1)/3)=cosπ(33/3)=cosπ(10+1)=-1

cosπ((2⁶+1)/3)=cosπ(65/3)=cosπ(21+2/3)=cosπ(21,666666666666667)=cosπ(1,666666666666667)=½

cosπ((2⁷+1)/3)=cosπ(129/3)=cosπ(42+1)=-1

cosπ((2⁸+1)/3)=cosπ(257/3)=cosπ(85+2/3)=cosπ(85,666666666666667)=cosπ(1,666666666666667)=½

…

Hiermee is gedemonstreerd dat de golflengte ook gerelateerd kan zijn aan de intensiteit van één stap met een factor (in het voorbeeld is dit afwisselend het getal 1 en 1+2/3=1,666666666666667) van π. Dit geeft dan de schaal van de grafiek op de n-as.

We kunnen de gehele getallen g in cosπ(g+ε) oplijsten: cosπ(0+1), cosπ(1), cosπ(2+1), cosπ(5), cosπ(10+1), cosπ(21), cosπ(42+1), cosπ(85), cosπ(170+1), …

De reeks 1, 1, 3, 5, 11, 21, 43, 85, 171, … is bekend als de Jacobsthal getallen en beschreven in OEIS A001045

Noem nu de reeks J₁, J₂, J₃, … dus J₁=1, J₂=1, J₃=3, J₄=5, J₅=11, … dan geldt dat J_n+J_n+1=2ⁿ, bijvoorbeeld: J₄+J₅=2⁴=16. Er geldt ook dat voor n>1 dat J_n=J_n-1+2J_n-2.

Dit is een gevolg van het aantal golven dat modulo m=2ⁿ gerealiseerd wordt. Zo verwachten we dat nog andere reeksen zullen kunnen beschreven worden doordat we gelijk welk aantal golven kunnen laten overeenkomen met 2π.

Nemen we enkel de waarden die een cosinus gelijk aan -1 opleveren, dan vinden we:

cosπ((2¹+1)/3)=cosπ(3/3)=cosπ(0+1)=-1

cosπ((2³+1)/3)=cosπ(9/3)=cosπ(2+1)=-1

cosπ((2⁵+1)/3)=cosπ(33/3)=cosπ(10+1)=-1

cosπ((2⁷+1)/3)=cosπ(129/3)=cosπ(42+1)=-1

cosπ((2⁹+1)/3)=cosπ(513/3)=cosπ(170+1)=-1

…

We herkennen terug de reeks 2, 10, 42, 170, 682, 2730, 10922, 43690, 174762, 699050, 2796202, 11184810, 44739242, 178956970, …, (2/3)(4ⁿ-1)). Dit zijn de partiële sommen van de oneven machten van 2 en zijn bekend als de reeks A020988 van de Sloane “On-Line Encyclopedia of Integer Sequences” (OEIS). De binaire voorstelling van deze getallen is 10, n maal achter elkaar (bijvoorbeeld 42 is in binair formaat 101010 en is het derde getal in de reeks, 170 is in binair formaat 10101010 en is het vierde getal in de reeks). Dit is, zoals daar aangetoond gerelateerd met een drievoud en het aantal atomen in een universum met oneven aantal onderscheidingen, want 2³=2*3+2, 2⁵=10*3+2, 2⁷=42*3+2, 2⁹=170*3+2, …. Inderdaad: 3J_n=2ⁿ-(-1)ⁿ. Bijvoorbeeld voor n=5: 32+1=33=3x11 en J₅=11.

Hieronder de tabel voor een maximaal aantal golven tot 37 (willekeurig gekozen) in de modulo m sequentie. Merk op dat 27 niet anders is dan 37 modulo 32.

Deze tabel demonstreert de volgende interpretatie: veronderstel dat elke kolom het onderscheidend vermogen geeft van een ander agens-in-context (bijvoorbeeld een agens geholpen door een andere instrumentatie voor waarnemen), toch zullen ze tot de conclusie kunnen komen dat ze periodieke verandering waarnemen, elk met een andere periode, een andere modulariteit. De meest primitieve verandering is de overgang van “ja” in “neen” (dus 1 afwisselend met 0, de meest linkse kolom). De meest onderscheidende verandering (de meest rechtse kolom) is a priori niet beperkt en niet gekend. Om dat te kunnen voorstellen moeten we wel een keuze maken en dat hebben we dus in de tabel gedaan. We kunnen er altijd van uitgaan dat er meer onderscheidingen noodzakelijk zijn, maar dat zal er ons niet van weerhouden om, door gebruik te maken van minder onderscheidingen, met elkaar te communiceren enkel door individueel een aantal golven te tellen en dat als schaalfactor te gebruiken voor een a priori onbekend aantal toestanden. Elk agens-in-context moet dat niveau waarop communicatie mogelijk wordt wel voor zichzelf creëren.

Een golfpakket

Wat de tabel met de hypothetische golven ook demonstreert is dat de amplitude van de golven met hoogste frequentie gemoduleerd wordt door golven met lagere frequentie. Deze modulatie gebeurt door de golven van de aanliggende resoluties en is bij sommige selecties van aantal golven duidelijk te zien. Dit betekent dat er altijd een schaal te vinden is waarop een golf door een andere golf gemoduleerd wordt en er dus een golfpakket ontstaat.

Modulatie is het gevolg van de goniometrische gelijkheid cos(a+b)+cos(a-b)=2cos(a)cos(b). In deze gelijkheid zien we de interferentie cos(a+b)+cos(a-b) van twee golven die gelijk is aan een verhouding 2cos(a)cos(b) die we kunnen interpreteren als een intensiteit vermenigvuldigd met een eenheid. Dus één van de beide cosinussen interpreteren we als intensiteit van de andere cosinus en die eenheid is dus “gemoduleerd”. Hetzelfde kunnen we uitdrukken door de vergelijking cos(p)+cos(q)=2cos((p+q)/2)cos((p-q)/2) met de transformatie a=(p+q)/2 en b=(p-q)/2. De factor 2 speelt in deze een belangrijke rol en verklaart waarom we machten van 2 gebruiken om de mogelijkheden van het model van golven te onderzoeken. Dit kunnen we als volgt inzien.

Veronderstel a=b, dus cos(2a)+cos(0)=2cos²(a). Dus cos(2a)=2cos²(a)-1=(√2cos(a)+1)(√2cos(a)-1). Dus cos(2a) is een verhouding van twee termen die elkaar moduleren. Dus een perfecte cosinuscurve met amplitude tussen +1 en -1 ontstaat als gevolg van een product van twee cosinuscurves met gerelateerde amplitudes zodanig dat het nulpunt zich enerzijds bevindt op cos(a)=(-1/√2) en anderzijds op cos(a)=(+1/√2). Dit is niet anders dan cosπ(1+1/4) en cosπ(0+1/4).

Maak nu cos(2a)+cos(a)=2cos²(a)+cos(a)-1=(√2cos(a)+√2)(√2cos(a)-√2/2). De interferentie van cos(2a) en cos(a) is een wederzijdse modulatie van (√2cos(a)+√2) en (√2cos(a)-√2/2), een term met nulpunt cos(a)=(-1) en een term met nulpunt cos(a)=(+1/2). Dit is niet anders dan cosπ(1+0)=cosπ en cosπ(1+2/3)=cos(π/3).

Veronderstel nu b=2a in de identiteit cos(a+b)+cos(a-b)=2cos(a)cos(b), dus cos(3a)+cos(-a)=2cos(a)cos(2a). Dus cos(3a)+cos(-a)=cos(3a)+cos(a)=2cos(a)(2cos²(a)-1)=4cos³(a)-2cos(a).

Dus cos(3a)=4cos³(a)-3cos(a)=cos(a)(4cos²(a)-3). We zien hier dat cos(a) de kwadratische vergelijking (4cos²(a)-3) moduleert of omgekeerd.

De interferentie van cos(3a) en cos(2a) wordt gegeven door de derdegraadsvergelijking cos(3a)+cos(2a)=4cos³(a)+ 2cos²(a)-3cos(a)-1

We kunnen verder afleiden:

cos(4a)=cos(2²a)=2cos²(2a)-1=2(2cos²(a)-1)²-1=8cos⁴(a)-8cos²(a)+1 en dit is een kwadratische vergelijking in cos²(a) met reële wortels.

cos(4a)+cos(2a)=2cos²(2a)+cos(2a)-1=(√2cos(2a)+√2)(√2cos(2a)-√2/2)=(√2(2cos²(a)-1)+√2)(√2(2cos²(a)-1)-√2/2)=(2√2cos²(a)(2√2cos²(a)-3√2/2)=4cos²(a)(2cos²(a)-3/2) dus de interferentie van cos(4a) en cos(2a) is een wederzijdse modulatie van een term met nulpunt cos(a)=0 en een term met nulpunt cos(a)=√3/2. Dit is niet anders dan cosπ(1-1/2)=cos(π/2) en cosπ(1-5/6)=cos(π/6).

cos(5a)=cos(4a+a). We gebruiken nu de relatie cos(4a+a)+cos(4a-a)=2cos(4a)cos(a) om te besluiten dat cos(5a)=2cos(4a)cos(a)-cos(3a)=(16cos⁵(a)-16cos³(a)+2cos(a))-(4cos³(a)-3cos(a))=cos(a)(16cos⁴(a)-20cos²(a)+5) en cos(a) moduleert een kwadratische vergelijking in cos²(a) met reële wortels of de kwadratische vergelijking moduleert cos(a).

cos(6a)=2cos²(3a)-1=32cos⁶(a)-48cos⁴(a)+18cos²(a)-1 en dit is een derdegraadsvergelijking vergelijking in cos²(a).

cos(7a)=cos(6a+a) enz…

cos(8a)=cos(2³a)=2cos²(2²a)-1 enz...

…

We zien een patroon ontstaan bij een even of een oneven factor voor a.

We zien ook een patroon ontstaan bij een factor voor a gelijk aan een macht van 2, de factoren waarmee we de tabel gebouwd hebben die de verschillende golven als hypothesen demonstreert.