Door toestanden te onderscheiden en deze te relateren aan onderscheidingen universa zijn we in staat een gedrag op een bepaalde schaal te modelleren door een representatie in een gekozen onderscheidingen universum. Het gedrag wordt dan beschreven in een toestandsruimte (fase ruimte) en als ordeningsparameter van het gedrag kunnen we de tijd nemen. Het aantal toestanden kan voortdurend toenemen, maar dat betekent niet dat het relevante onderscheidingen universum steeds moet toenemen: het kan zowel toenemen als afnemen. De intensiteit van een onderscheidingen universum kan evolueren.

Dit kunnen we grafisch voorstellen: we zullen toestandsovergangen (minstens) twee dimensionaal voorstellen in een “fase diagram” (Poincaré plot) waar de intensiteit van één toestand op de x-as voorgesteld wordt en de intensiteit van de volgende toestand op de y-as. Zo wordt het traject in de tijd naar bijvoorbeeld een evenwicht duidelijk (in het traject naar evenwicht zijn oscillaties mogelijk en bij evenwicht zijn de opeenvolgende intensiteiten dezelfde). “Poincaré plots” worden gebruikt om ogenschijnlijk chaotische processen toch te karakteriseren, immers terwijl een volledig chaotisch proces in een fase diagram zal voorgesteld worden door een wolk punten die alle relevante intensiteiten toont en een willekeurig verband tussen de intensiteit op het ene en het andere moment, zal een ogenschijnlijk chaotisch proces (zoals ze bijvoorbeeld ontstaat met de logistische relatie) enkel punten in een bepaald gebied vertonen (een attractor genoemd) en relaties tussen die punten kunnen dan gevisualiseerd worden, bijvoorbeeld voor twee en drie opeenvolgende toestanden. Het hoeft ons dan ook niet te verbazen dat we de schaalfactoren 2ⁿ terugvinden “op het traject naar chaos” voor de logistische relatie waarbij bifurcaties (verdubbelingen) voorkomen en op verschillende schalen hetzelfde patroon te herkennen valt (fractalen).

We zijn nu in staat een nieuw voorbeeld van orthogonaliteit te demonstreren: de schaalfactor 2ⁿ kan gekozen worden los van het aantal elkaar uitsluitende toestanden, maar wordt door het minimale aantal wel beperkt en het aantal elkaar uitsluitende toestanden kan toenemen zonder dat we de schaalfactor willen of kunnen veranderen. Merk op: de schaalfactor kan toenemen of afnemen, het aantal toestanden neemt uitsluitend toe. De modellering van een simultaneïteitsinterval dat alleen maar toeneemt zal aanleiding geven tot een nieuw model dat in staat is de bekende Lorentz transformatie te modelleren.

We kunnen ons nu voorstellen dat de momentaan ervaren punten een toestandsruimte opspannen van potentiële punten, punten die dus allemaal hypothetisch zijn, behalve het momentaan ervaren punt. Binnen die toestandsruimte zou een entiteit dus een hypothetische baan kunnen volgen die zijn gedrag weergeeft. Een as die de toename van toestanden modelleert, orthogonaal met de as die het aantal schaalfactoren weergeeft, zou immers de evolutie van die toestandsruimte kunnen weergeven, en hierbij kunnen we dan weergeven hoeveel onderscheidingen relevant zijn en hun relevantie verliezen of niet relevant zijn en hun relevantie verkrijgen.

Een voorbeeld van zo’n evolutie is dan een ontwerpproces met zijn inherente ontwerpparadox waarin we twee banen zien, de evolutie (in de tijd) van intensiteiten van een toestandsruimte op een bepaalde schaal (in de grafiek voorgesteld als punt). De ene is die van maximale relevant geachte (dus gekozen) disjunctie (repertorium 1), de andere van maximale relevant gebleken conjunctie (repertorium 2) in de loop van de tijd. Het is duidelijk dat die intensiteit een astronomisch groot getal kan zijn maar dat ontwerpers toch in staat zijn enkel de relevante toestandsruimte op het spoor te komen door nieuw te ervaren prototypes te creëren zodanig dat alle stakeholders aangesproken worden in hun eigen repertorium. De ontwerpers kunnen dan, door de analyse van de acties van de stakeholders met de prototypes, de relevante onderscheidingen van de irrelevante onderscheiden voor elk van de betrokken stakeholders (en zo kennis opbouwen).

Een eenvoudige Poincaré plot die het verband toont tussen wat er beslist werd om als mogelijkheid te behouden om er iets uit te leren (bij een volgende stap) kan er dan als volgt uitzien:

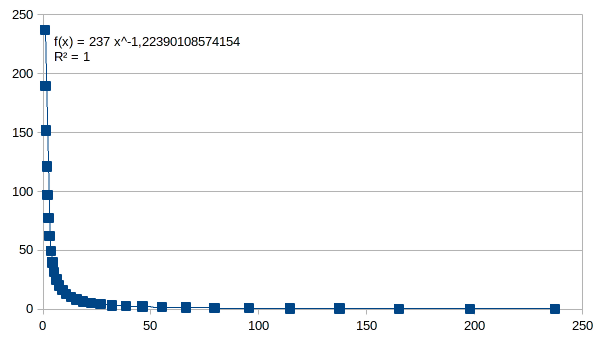
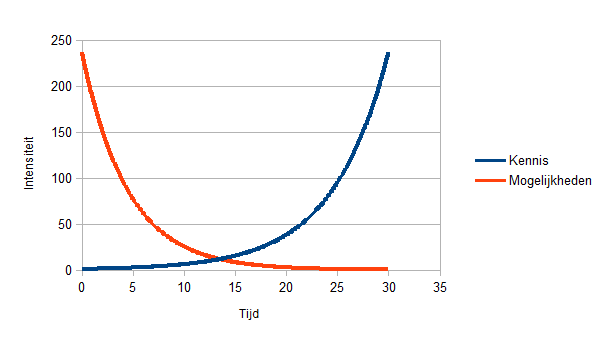
Veel mogelijkheden en weinig kennis in een begintoestand worden gevolgd door een toestand van minder mogelijkheden en een kleine toename van kennis omdat bij het reduceren van mogelijkheden in een beslissing om iets te testen zeker iets zal duidelijk worden in een volgende stap, maar nog niet erg veel. Naarmate er beslist wordt om mogelijkheden verder te reduceren kan de kennis erg toenemen omdat elk beetje opgebouwde kennis natuurlijk veel mogelijkheden al simultaan kan uitsluiten. Op het einde van het proces blijven niet veel mogelijkheden over, maar is er wel exponentieel meer kennis gewonnen bij elke stap.

Er wordt sinds het midden van de vorige eeuw veel onderzoek gedaan naar “complexe adaptieve systemen” die kunnen blijven co-evolueren omdat ze er in slagen gebruik te maken van enerzijds stabiliteit op verschillende schalen en anderzijds verandering op de “rand van chaos”, die zich op elke schaal anders voordoet. Dit voorbeeld maakt duidelijk dat het ontwerpproces bij uitstek hiervan een voorbeeld is en dat een lineair ontwerpproces de eenvoudige Poincaré plot vertoont die hierboven gedemonstreerd werd.

In tegenstelling met het voorbeeld zal niet elk ontwerpproces lineair verlopen en zal dus eerder de Poincaré plot van een “strange attractor” vertonen.