Een agens ageert. De focus van zijn actie wordt in het haakformalisme als een symbool voorgesteld. Bijvoorbeeld F. Sommige agentia moeten het symbool niet ervaren, ze moeten niet ageren, ze kunnen F manipuleren zonder er een ervaringswaarde aan toe te kennen. Dat manipuleren is volledig coherent met het ervaren. Formeel: F kan niet onderscheiden worden van F↔<>. Dit is hetzelfde als <F>↔<<>>, wat de actie formeel uitdrukt. <> en <<>> staan voor de onderscheidbaarheidsgrens van het agens dat F als mogelijkheid van focus heeft. Selecteert het agens het symbool F dat staat voor een bepaalde structuur, dan gebeurt er ook iets anders. Die structuur noemen we “een bepaalde orde” omdat, wanneer één F gekozen wordt uit een mogelijk vrij te kiezen repertorium er simultaan andere foci gekozen worden. Iets anders dan F kan gelijk wat zijn, behalve F. Het ervaren van een orde in een bepaald (deel)universum F doet DUS onvermijdelijk het gebeuren van “iets anders dan DEZE orde” (noem dit wanorde of chaos) toenemen in een groter universum waarin F een mogelijke focus is. Zowel F↔<> als <F>↔<<>> is de formele uitdrukking van een proces dat doorlopen wordt door een ervarend agens. We kunnen dus stellen: geen orde zonder chaos, geen chaos zonder orde. Om dit heel concreet ervaarbaar te maken kan het experiment met het werpen van een dobbelsteen gebruikt worden: waarnemingen die vanuit een bepaalde focus beperkt zijn, perfect geordend zijn en voorspelbaar zijn, zijn volledig willekeurig (waarschijnlijkheid 50%) vanuit een andere focus. Er is altijd een keuzevrijheid van focus, maar dan moet die wel effectief gekozen worden om orde te kunnen waarnemen. Dit is niet anders dan het inzicht in simultaneïteit.

Een proces (in de tijd) kunnen we labelen omdat we unieke toestanden kunnen onderscheiden die een conjunctie zijn met een laatst toegevoegde onderscheiding bovenop de (n-1) onderscheidingen van het universum dat door die (n-1) onderscheidingen opgespannen wordt. Er zijn dan telkens weer 2ⁿ unieke gebeurtenissen te onderscheiden, waarvan er zich maar één effectief voordoet, een gebeurtenis die op dat unieke moment het supremum is van een universum dat voor alles, behalve die ene onderscheiding, stabiel is. Voor elk punt uit een n-onderscheidingen universum geldt dan dat het in functie van de unieke laatste onderscheiding ℵ (of met die ℵ als standpunt) kan geschreven worden door de bitstring van het punt te splitsen in twee even lange delen die we p en q noemen. Voor een punt dat blijft bestaan in de tijd (en dat noemen we dan "stabiel" omdat het waargenomen kan worden) zijn de delen p en q dan de stabiele delen, de ℵ is variabel wat betekent dat die ℵ verandert (“van waarde”). Zowel p als q worden dan door dezelfde (n-1) onderscheidingen opgespannen. Dus door een bitstring op deze manier in twee delen te splitsen en beide delen met elkaar te vermenigvuldigen (wat XOR of de vector vermenigvuldiging afbeeldt modulo3, formeel dus door p•q te vormen) krijgen we een uniek punt (op een gemeenschappelijke factor c na, want p•q is niet anders dan (c•p)•(c•q)) in een onderscheidingen universum met één onderscheiding minder dat het stabiel gebleven en dus ervaren punt kan afbeelden en dat we de afgeleide genoemd hebben, een vorm die geconstrueerd wordt uit een focus die op een factor na bepaald is. De onderscheiding die de unieke gebeurtenissen uniek kan labelen is voor die stabiele string irrelevant. Dit is de onderscheiding die we als tijdsparameter t benoemd hebben maar we hebben dat ook tot gelijk welke vrijheidsgraad uitgebreid (de vrije keuze van stap T). We moeten dit goed begrijpen: van de 2ⁿ punten (AND-atomen) die elkaar uitsluiten kan er zich maar één voordoen en dit punt wordt dus door de AND met die ℵ voorgesteld. Welk AND-atoom nu wel gerealiseerd werd is onvoorspelbaar en volledig onbelangrijk, het kan er maar één zijn, maar die ℵ is de laatst toegevoegde onderscheiding en dat is de “parameter tijd”. Voor de duidelijkheid nog eens herhalend: exact hetzelfde kan ook duaal uitgedrukt worden door OR-atomen te benoemen die gebeuren in de tijd. Het uniek punt dat wel relevant is, is het punt in het onderscheidingen universum met één onderscheiding minder, het is het stabiel punt dat simultaan ervaren wordt tijdens het ervaren van de unieke vluchtige momenten die dus een unieke labeling kregen door een getal dat geïnterpreteerd kan worden als de waarde van een parameter en daardoor kan dit uniek punt begrepen worden als het nulpunt of standpunt waaruit men de werkelijkheid waarneemt. Het stabiel en enige uniek punt p•q is in die interpretatie dus niet te onderscheiden van <>, zijn inbedding is niet te onderscheiden van <<>>.

Er zijn dus (onvermijdelijk potentiële) universa (en dus hypothesen) mogelijk waarbij het onmogelijk is op voorhand te voorspellen welke toestand van de 2ⁿ mogelijke toestanden zal gerealiseerd worden en dat ondanks het feit dat die universa door een stabiel aantal onderscheidingen opgebouwd worden. Dit betekent dat het onvermijdelijk is dat er chaotische processen zullen blijven onderscheiden worden. In de tijd gaat men dan van een bepaald n-onderscheidingen universum naar een ander m-onderscheidingen universum, gekarakteriseerd doordat n-1 onderscheidingen onveranderd blijven gebruikt worden in al deze universa en enkel de laatst toegevoegde niet ingebouwd wordt. Een willekeurig dynamiek kan dus onderzocht worden met behulp van “de vluchtige laatste onderscheiding”, dit is een onderscheiding die niet ingebouwd wordt in een bestaande structuur en daardoor kan modelleren dat structuren veranderen, dus dat er zoiets kan ontstaan als tijd: iets is vluchtig en iets blijft. Een tijdsvariabele is een potentiële onderscheiding die enkel in het ervaren een waarde krijgt als de intensiteit van de laatst toegevoegde onderscheiding en waarvan de waarde iets kan vertellen over wat stabiel blijft in het ervaren. Het begrip “tijd” is onvermijdelijk verbonden aan een 1-splitsing met een laatst toegevoegde onderscheiding.

We merken nu op dat een chaotisch en dus onvoorspelbaar proces niet betekent dat zo'n proces niet te modelleren zou zijn, wat we hieronder willen demonstreren. Hierbij moet men natuurlijk niet verwachten dat deze modellering een model zou zijn van enig anticipeerbaar proces, het is de modellering van chaos, en chaos betekent juist de naam die we geven aan een in werkelijkheid niet te anticiperen proces, een proces dat we willekeurig noemen. Willekeurige processen zijn heel belangrijk als we zekerheid willen krijgen over datgene dat wel stabiel zal blijven, en dat herkennen we in alle procedures die een bruikbare waarschijnlijkheid opleveren.

Een chaotisch en dus onvoorspelbaar proces kan in het haakformalisme geconstrueerd worden door de begrenzing van de eigenwaarde uit te drukken, wat ons niet moet verwonderen aangezien we begrepen hebben dat chaos onvermijdelijk waargenomen zal worden wanneer men de mogelijke foci die men kan innemen beperkt. De entiteit (x-x₀) is begrensd, de intensiteit van (x-x₀) kan onbegrensd zijn. Indien men dus de intensiteit begrenst dan genereert men effecten die enkel als chaos kunnen begrepen worden. Inderdaad: de eigenwaarde k (die zich tussen 0 en 1 bevindt als men het gedrag van de intensiteit van een entiteit wil modelleren en de spontane verandering ervan) kan men evenzeer als een verschil begrijpen, een verschil met de inherente grenzen van het getal k, namelijk enerzijds 0 en anderzijds 1. In plaats van k of 1-k te gebruiken, gebruiken we nu als eigenwaarde voor het proces het product van beide: het product namelijk van het verschil met een minimale situatie (namelijk k-0) en met het verschil met een maximale k (namelijk 1-k). Dit product is goed gefundeerd. Dit leidt tot de recurrente relatie van het veranderen van de intensiteit van k: (k-0)_(t+Δt)=r(k-0)_(t)(1-k)_(t) waarbij r een willekeurige constante is (ook uitdrukbaar als een verhouding tussen de grenzen). Dit is de eigenwaarde van de verandering van de k gegeven door (k-0)_(t+Δt)=r(k-0)_(t), maar bij elke stap gewogen door (1-k)_(t). Van deze relatie is bekend dat ze voor een waarde van r gelijk of hoger dan 3 een chaotisch gedrag modelleert.

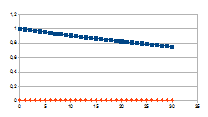
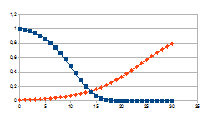
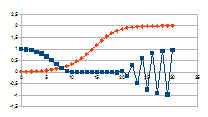
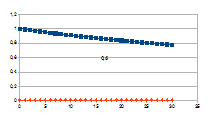
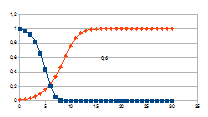
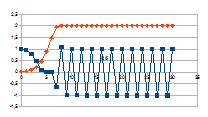
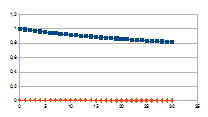
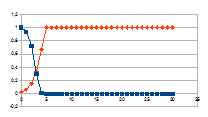
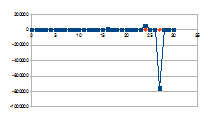
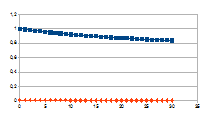
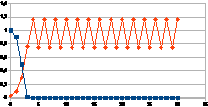
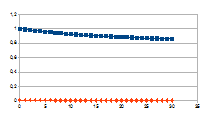
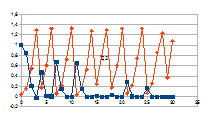
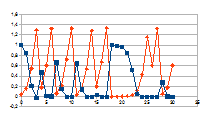
Hierbij het gedrag over dertig stappen voor een k tussen 0,01 en G-k met G variërend tussen 0 en 2 van de intensiteit van rk(G-k)=j (datapunten met ruit) die resulteert in een verandering van de intensiteit van een entiteit gegeven door de negatieve feedback 0+(1-j)ⁿ (datapunten met vierkant).

De grafieken tonen inderdaad het chaotisch gedrag van de intensiteit van de entiteit (x-x₀), gedrag dat resulteert uit het chaotisch gedrag van de verandering van de intensiteit van de eigenwaarde.

Gevoeligheid voor de beginvoorwaarde

De benadering langs het haakformalisme laat toe een ander zicht te werpen op de "gevoeligheid voor de beginvoorwaarde" die geleid heeft tot een een nieuw onderzoeksgebied: de deterministische chaos theorie. De ontdekking van de praktische onbepaaldheid van de baan van sommige hemellichamen dateert al van de negentiende eeuw toen Henri Poincaré unieke oplossingen probeerde te vinden voor het algemeen drielichamenprobleem maar werd door Edward Lorenz ook voor andere processen met een beperkt aantal parameters aangetoond.

Een operationeel te gronden feedback hebben we gemodelleerd als (x-x₀)_(t+Δt)=k(x-x₀)_(t) met -1<k<1. De veronderstelling is: (x-x₀) is een entiteit die wat betreft zijn intensiteit verandert met een factor k.

Wanneer we deze veronderstelling verlaten en we het verschil (x-x₀) nu niet meer als een constante beschouwen, kunnen we de veronderstelling van de klassieke differentiaalrekening reconstrueren. We beschouwen dan als de enige gekende constante de waarde x₀, en we noemen dit de beginvoorwaarde, en gaan ervan uit dat die niet verandert in de tijd (is dus constant voor alle stappen). De vergelijking zegt dan dat de toename van de waarde x (die een variabele is en geen entiteit) met één tijdstap gelijk is aan een fractie van de waarde x op dit moment, gecorrigeerd met een onbekende constante term k (dat noteren we dan als kx_t). Met de formele conventionele schrijfwijze is dit dx/dt=kx waarbij op tijdstip nul geldt dat x=x₀ en dit is het enige moment waarop de constante term gekozen kan worden, want dan zijn beide leden van (x-x₀)_(t+Δt)=k(x-x₀)_(t) simultaan nul. De variabele dx is een onderscheiding, wat we zeer helder uit het haakformalisme zelf kunnen afleiden, en de factor waarmee dx vermenigvuldigd wordt is de afgeleide van de functie x in het punt t=t.

We kunnen het inzicht dx/dt=kx nu anders schrijven als dx/x=kdt. Als we beide leden integreren vinden we ln|x|=C+kt waarbij C een willekeurige constante is. Let op het noodzakelijk gebruik van de absolute waarde aangezien de natuurlijke logaritme enkel voor positieve getallen gedefinieerd is.

Dus kunnen we beide leden van de vergelijking met een exponentiële functie e^z op een unieke manier (e^z is een bijectieve functie) transformeren:

e^ln|x|=e^C+kt of |x|=±e^Ce^kt, let op het gebruik van ±. Wanneer we in deze vergelijking t=0 nemen dan vinden we |x|=±e^Ce^k0=±e^C=x₀. Men kan de beginvoorwaarde (t=0) dus langs de negatieve kant of langs de positieve kant benaderen, wat in onze grafische voorstelling van negatieve en positieve feedback op een operationele vanzelfsprekende manier gegrond is. We hebben dat ook op nog een andere manier kunnen aantonen door gebruik te maken van een structuur m die we dan ook een Lorentz invariant genoemd hebben (maar dan ter ere van Hendrik Lorentz, winnaar van de Nobelprijs voor Natuurkunde in 1902). De structuur m is constant voor alle stappen en is dus niet meer waarneembaar bij een verschil tussen stappen. Wat we dan aantonen is dat, wanneer we voor m een negatief getal kiezen, we kunnen zien hoe dit een rol speelt bij het berekenen van tijdsverschillen. Tijdsverschillen zijn de klassieke tijdsmetingen en verbergen daardoor dus een essentieel element van de werkelijkheid.

De oplossing voor een variërende x is dus in zijn algemene vorm niet verschillend van x=±D±x₀e^kt met -1<k<1 en de onbekende D die van tijdstap tot tijdstap kan verschillen. We kunnen dat in een eenvoudiger vorm evenzeer schrijven als x₀(E±e^±kt) met 0<k<1 en E verschillend van 1, waarbij E ook van stap tot stap verschilt.

De gevoeligheid voor de beginvoorwaarde zegt dus dat er voor sommige variabelen x (en dat is dus niet een entiteit maar het is een intensiteit of een getalfunctie als relatie van intensiteiten, functie waarvoor een afgeleide kan gevonden worden die een zekere eigenwaarde k genereert die de intensiteit van een entiteit kan weergeven) een entiteit (x-x₀) te vinden is waarbij de geanticipeerde evolutie van zijn intensiteit inherent onvoorspelbaar is omdat de constante D (of E) a priori onbekend is. En dat is niet anders dan het basisinzicht dat iets anders dan F gelijk wat kan zijn, behalve F.

Door de simulatie met de logistische differentievergelijking is ook duidelijk hoe dit te maken heeft met de grenzen van de intensiteit van een mogelijke entiteit.