Elk proces gedraagt zich als een klok
die gekarakteriseerd wordt door processtappen. De stappen bepalen de
toestanden (die elkaar dus uitsluiten) en dus de resolutie. De sporen
van de klok worden per processtap gegenereerd, zij sluiten elkaar
uit. Het verdubbelen of halveren van de intensiteit van de sporen
meet
“tijd” voor dit proces. De relevante tijdstap (globaal, k=1
en lokaal, k=k) wordt dus afgeleid vanuit het waarnemen van (elkaar
uitsluitende) toestanden (van en door entiteiten die agentia zijn) in
het proces en wordt niet a priori geponeerd. We tellen de toestanden
discontinu.
Dit heeft praktische gevolgen als men zonder kritische houding
uitgaat van het a priori van continuïteit. Continuïteit is immers
operationeel niet te realiseren (als toestanden die elkaar uitsluiten
waartussen een verschil kan gemaakt worden) en dat betekent dat het
eigenlijk een constructie is (“indien…, dan...”). Als men op
basis van twee metingen ervan uitgaat dat er datapunten kunnen
geanticipeerd worden “tussen” deze twee (met een lineair verband
of niet, minimaal dus een differentieerbaar verband) dan
veronderstelt men een continuïteit die misschien niet waarneembaar
is, men veronderstelt punten waartussen een agens een verschil kan
maken terwijl dat in werkelijkheid niet zo is, hypothese die
misschien zal leiden tot waarnemingsparadoxen.
Door discontinu sporen te tellen houden we dus rekening met de
waarnemingsgevoeligheden of waarneming resoluties van
agentia-in-context. De continuïteit-discontinuïteit verschil is
goed te modelleren door een rotatie, door een
frequentie van zekerheid.
Bij ons algemeen
onderzoek naar processen hebben we de waarden op de abscis
geïnterpreteerd als tijdstappen. Dat is een eenvoudige conventie,
maar slechts een conventie. We kunnen evenzeer de waarden op de
ordinaat als stappen gebruiken zodanig dat ze als de waarneembare
stappen in intensiteit kunnen geïnterpreteerd worden (en dus als
verschillen die een verschil maken voor het agens-in-context), we
zouden exact dezelfde curve bekomen met datapunten die de relatie
geven tussen abscis en ordinaat. Maar helemaal verhelderend is het om
daarenboven ook de eenheid op de assen te transformeren. In plaats
van de waarden te interpreteren als bijvoorbeeld m*1=(1±k)n*1
met n lineair op de abscis, en 1 de eenheid op de as, kunnen we ook
schrijven logm+log1=nlog(1±k)+log1 en dus n=logm/log(1±k), met m
lineair op de abscis. Lineaire toenames zijn gemakkelijker te
interpreteren en we hopen dan dat het inzicht zal volgen dat er niets
absoluut aan tijd. De abscis geeft dan de intensiteit en de ordinaat
geeft dan de overeenkomstige processtap n waarbij die intensiteit
geanticipeerd wordt (in de toekomst) of gereconstrueerd wordt (in het
verleden). Verleden is hier te interpreteren als de aspecten die
noodzakelijk zijn voor het “nu” en de toekomst is te
interpreteren als de aspecten waarvoor het “nu” noodzakelijk is.
De transformatie met de logaritme maakt van een exponent een lineaire
parameter (met coëfficiënt 1±k), volledig in overeenstemming met
de manier waarop we een
ongekende eenheid (processtap) willen meten die enkel toeneemt of
enkel afneemt. Noteer dat de logaritme enkel gedefinieerd is voor
positieve getallen.
Hieronder de basispatronen die ontstaan voor k=0,2 met vierkant
symbool en k=0,3 met ruitsymbool en dertig stappen in intensiteit. In
beide gevallen hebben de laagste intensiteiten de grootste
verandering nodig van aantal processtappen. Noch de waarden voor de
logm/log(1+k) als de waarden voor logm/log(1-k) zijn asymptotisch en
we herkennen een positieve feedback in de twee gevallen. De curve kan
voor grote intensiteiten goed benaderd worden als een lineaire
toename.
logm/log(1+k)
|
Wordt groter vanaf 0 naar verdere +
|
Positieve feedback in de positieve zin. Grotere intensiteit komt
overeen met een tijdstip verder in de toekomst
|
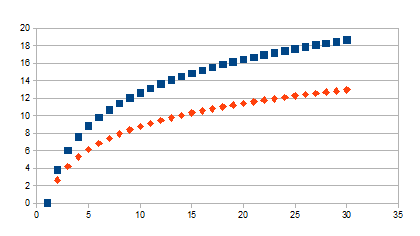
|
logm/log(1-k)
|
Wordt kleiner vanaf 0 naar verder -
|
Positieve feedback in de negatieve zin. Grotere intensiteit komt
overeen met een tijdstip verder in het verleden
|
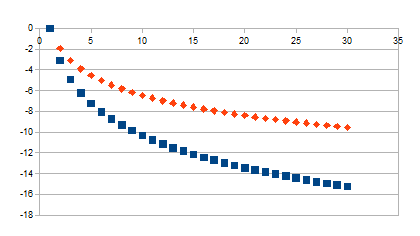
|
We merken nu op dat, wanneer ook de intensiteiten tussen 0 en 1
geplot worden de nul asymptotisch benaderd wordt en er dan een
exponentieel veel groter verschil in processtappen overeenkomt met
een kleine intensiteitswijziging. Welke klok we ook zouden gebruiken,
in een ver verleden “liep ze trager”, wat betekent dat de
resolutie niet gepast is om kleine intensiteitswijzigingen waar te
nemen. Bijvoorbeeld: de verdubbeling van de intensiteit van een
buffer had niet waargenomen kunnen worden omdat de klok dat niet kon
genereren, ze genereerde bijvoorbeeld al onmiddellijk een
verviervoudiging.
Hieronder de patronen die ontstaan voor k=0,2 met vierkant symbool
en k=0,3 met ruitsymbool en zeventig stappen in intensiteit met een
intensiteitsverschil van 0,033. Voor de verschillende groottes van k
treedt een inversie op bij het nulpunt van de waarden (de eenheid van
de intensiteit).
logm/log(1+k)
|
De waarden gaan van de tijd in een ver verleden (constructie van
een mogelijk verleden) over een nulpunt in de tijd in de richting
van toenemende tijd (constructie van een mogelijke toekomst).
|
Positieve feedback in de positieve zin
|
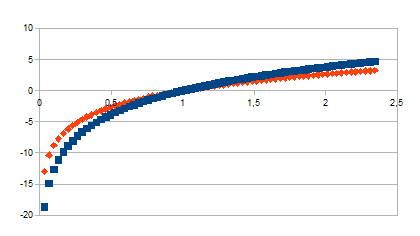
|
logm/log(1-k)
|
De waarden gaan van de tijd in een verre toekomst (constructie van
een mogelijke toekomst met een kleine intensiteit) over een
nulpunt in de tijd in de richting van afnemende tijd (constructie
van een mogelijk verleden met een grote intensiteit).
|
Positieve feedback in de negatieve zin
|
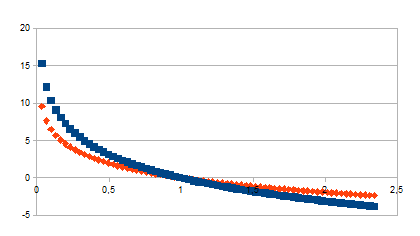
|
De lijn met ordinaat gelijk aan nul is het
“nu” van het agens, de werkelijk die voor het agens dringend
en belangrijk is. Het “nu” is het “ja” van de waarneming, en
tevens het “neen” van een andere waarneming. Het is de 100%
zekerheid: “dat spoor klasseer ik als het aspect dat aanwezig is
(of het “anders aspect” dat afwezig is)”. Het “nu” heeft
een bereik in het verleden en in de toekomst wat we kunnen modelleren
als de breedte van een band rond de abscis as. Het verschil tussen de
eenheid (1+k) en (1-k) is te merken in de intensiteiten die buiten de
waarneming vallen in die band: het verleden voor (1+k) en de toekomst
voor (1-k).
We kunnen nu de agentia met k=0,2 (vierkant) en k=0,3 (ruit) met
elkaar vergelijken. Een bepaald intensiteitsverschil komt voor de
kleinere k en dus kleinere onzekerheid overeen met een groter
tijdsverschil. Het agens met een kleinere eigenwaarde zal daarbij een
bepaalde intensiteit met een verder verleden verbinden maar
ook met een verdere toekomst (voor de twee soorten feedback)
vergeleken met een agens met een grotere eigenwaarde. Maar ook: een
agens die een kleiner verschil in intensiteiten kan waarnemen
(los van de eigenwaarde) zal een kleiner “nu” hebben. Als de
waarneming een groter verschil nodig heeft dan zal het “nu”
groter zijn vergeleken met het andere agens. Dit maakt de volgende
interpretatie mogelijk: een kleiner verschil in intensiteit
waarnemen kan doordat het agens de werkelijkheid met meer
onderscheidingen kan opspannen. Maar dat betekent ook dat er minder
zekerheid is over de waarneming. Wanneer we dat combineren met de
eigenwaarde (een grotere k betekent dat er een grotere onzekerheid is
in welke toestand het proces zich bevindt) kunnen we besluiten dat,
voor dezelfde werkelijkheid, met evenveel onderscheidingen dus, het
agens met de grotere eigenwaarde meer onzeker is zowel over verleden
als toekomst dan het agens met kleinere eigenwaarde en daarenboven
die toestand sneller bereikt. Het agens dat dan een kleinere
onzekerheid heeft (kleinere k) zal voor een zelfde
intensiteitsverschil pas later “gedwongen worden” om te reageren
op het verder toenemen van de onzekerheid en zal pas later actie
ondernemen (een waarneming uitvoeren en zo een collaps uitvoeren in
de opgespannen werkelijkheid) dan het agens met een grotere
eigenwaarde en dus grotere onzekerheid.
Door de inverse van de waarden te nemen is de singulariteit goed
zichtbaar.
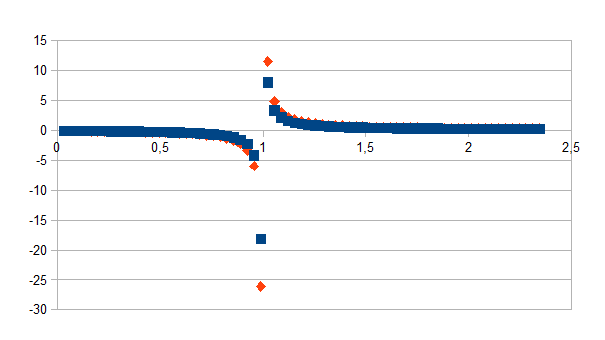
De
betekenis van de discontinuïteit op een onbegrensd grote
toekomst/verleden kan als volgt geïnterpreteerd worden. De
anticipatie naar positieve waarden van de tijd is een constructie. Er
zal in de toekomst ook altijd iets anders gebeuren dan datgene dat
kan geanticipeerd worden. De anticipatie naar negatieve waarden van
de tijd is eveneens een constructie, die gewoonlijk reconstructie
genoemd wordt omdat hier ook geldt dat niet alle aspecten van een
waarneming in het verleden kunnen ge(re)construeerd worden. Er zal in
het verleden ook altijd iets anders gebeurd zijn dan datgene dat kan
ge(re)construeerd worden. De anticipaties die verbonden zijn aan een
bepaalde waarnemingsresolutie (verschil dat een verschil maakt)
strekken zich zowel naar het verleden als naar de toekomst onbeperkt
uit.




