Door de intensiteit van een toestand
op twee verschillende stappen (“in de tijd”, “in de ruimte”)
aan elkaar te relateren door het model
(x-x0)(t+Δt)=k(x-x0)(t)
met -1<k<1, anticiperen we dat de intensiteit van “het
verschil dat een verschil maakt” verandert en dat de verandering
gemodelleerd wordt met een factor k die, in
een eerste benadering, een nieuwe constante is naast de
constante (x-x0). Daardoor hebben we een nieuwe entiteit
gecreëerd, namelijk de soort k(x-x0). Aangezien k=±1
overeenkomt met enerzijds geen, anderzijds een spontaan proces,
kunnen we de entiteiten die gekarakteriseerd worden door k(x-x0)
deelentiteiten (of telbare deelsystemen, telbare deelaspecten) noemen
van het spontaan proces. We hebben dan ook onderzocht hoe
de deelprocessen kwantitatief hun invloed zullen doen gelden
binnen het totaal spontaan proces. Sommen van processen leiden tot
S-curves en U-curves en door een selectie van de getallen in de
exponenten kunnen we hiermee “catastrofale”
gebeurtenissen modelleren, gebeurtenissen die gedurende een groot
aantal processtappen amper van intensiteit wisselen om dan plots
exponentieel gedrag te vertonen. Dit is een gedrag dat veelvuldig
waargenomen wordt in de natuur (fase overgangen tussen vast en
vloeibaar, zelfontbranding, het plots instorten van een zandhoop,
aardbevingen enz…). De processtappen waarbij dat gebeurt worden de
kritische punten genoemd: de specifieke combinatie van parameters
waarbij het nieuw gedrag (de catastrofe) optreedt. Dit wordt dikwijls
toegeschreven aan schaaleffecten en fractale organisatie en dat is nu
onze focus. We
merken immers op dat de intensiteit k(x-x0) op
een bepaalde stap kan geïnterpreteerd worden als “van de constante
(x-x0)” maar evenzeer “van de constante k”, beide
factoren van de intensiteit kunnen dezelfde rol spelen, maar dat is
niet volledig zo, wat zich uit in schaaleffecten (en dus
verhoudingen).
Schaaleffecten en meervoudigheid
Het model (x-x0)(t+Δt)=k(x-x0)(t)
is gebaseerd op de klassieke hypothese dat verhoudingen zin hebben,
maar ook op de vaststelling dat er niets absoluut is aan de stappen
“in de tijd” of “in de ruimte”, ze zijn agens-in-context
afhankelijk en de stappen zijn het gevolg van toestanden die
elkaar uitsluiten, waarneembaar door de geproduceerde sporen die
elkaar uitsluiten. Dus kunnen we ook de mogelijke <<intensiteit
of eenheid>> dus <<k of (x-x0)>>
beschouwen bij een gekozen aantal elkaar uitsluitende stappen
n. We hebben met
het algemeen product model inderdaad begrepen dat het product
(x-x0)Πν(1+κ) kan modelleren dat sommige
(1+k)m constanten zijn naast de constante (x-x0).
Het aantal processtappen dat we kiezen is gerelateerd met de
intensiteit van de eenheid (x-x0) die we gekozen hebben om
waar te nemen. We hebben immers al opgemerkt dat n als een
verdubbelingstijd
(of halveringstijd) kan geïnterpreteerd worden van de eenheid
onder focus. Dat we n als alternatief voor k kunnen zien is
gemakkelijk met een voorbeeld te illustreren.
Veronderstel de n (processtap of aantal toestanden) waarvoor
geldt in positieve feedback: (x-x0)(1+k)n=2(x-x0).
Dit is een verdubbeling van (x-x0). Hieruit volgt dat
n=(log2(1+k))-1 en die n zal evenzeer als k
het proces karakteriseren. Bijvoorbeeld voor een kleine k (stel
k=0,1) bekomen we een verdubbeling tussen de processtappen 7 en 8
want n=(log2(1,1))-1=7,2725408973.
Veronderstel de n (processtap of aantal toestanden) waarvoor
geldt in negatieve feedback: (x-x0)(1-k)n=2-1(x-x0).
Dit is een halvering van (x-x0). Hieruit volgt dat:
(1-k)n=2-1 waaruit volgt n=-(log2(1-k))-1.
Bijvoorbeeld voor een kleine k (stel k=0,1) bekomen we een halvering
tussen de processtappen 6 en 7 want n=-(log2(0,9))-1=6,578813479.
Het is altijd goed om zich hierbij expliciet te herinneren dat dit
in werkelijkheid zin moet hebben (denk aan het voorbeeld: een
halve koe is geen koe maar een kadaver en het proces waarbij we
na één koe waargenomen te hebben ook een tweede koe waarnemen is
het proces waarvan we de stappen veronderstellen, en dit heeft
uiteraard niet alleen met tijd te maken maar met een bepaalde
agens-in-context die zeer complexe toestanden kan meemaken).
Het inzicht om de eigenwaarde te interpreteren als een aantal
stappen waarbij verdubbeling optreedt kan gemakkelijk uitgebreid
worden. Bijvoorbeeld voor dezelfde kleine k (stel k=0,1) bekomen we
een verdrievoudiging tussen de processtappen 11 en 12 want
n=(log3(1,1))-1=11,5267046072476. Dus een
ver-m-voudiging voor dezelfde kleine k zal op treden rond stap
n=(logm(1,1))-1. Hierin is n een reëel
positief getal dat zich altijd tussen twee gehele getallen bevindt
(het zijn gehele getallen die geteld worden). Voor m en een positieve
feedback is het kleinste getal m=2, één stap waarbij dus één
extra eenheid gemaakt wordt en dit komt overeen met een eigenwaarde
k=1, want 1=(log2(1+1))-1. Voor m en een
negatieve feedback is het grootste getal: m=2-1, één
stap waarbij dus de helft van alle eenheden verloren gaat en dit komt
overeen met een eigenwaarde k=-2-1, want
1=-(log2(1-2-1))-1. We tellen,
discontinu dus, entiteiten en dat hangt af van de processtappen die
we eveneens discontinu kunnen tellen. Het aantal stappen waarbij
verdubbeling of halvering optreedt is een alternatieve maat voor de
eigenwaarde. Dus naarmate n toeneemt (afneemt) kunnen er ook meer
entiteiten ontstaan (verdwijnen) en dat is waar te nemen als
gerelateerd tot de intensiteit van het gekozen verschil dat een
verschil maakt, de intensiteit van de eenheid (x-x0). “De
entiteit” vullen we niet specifieker in met een a priori
interpretatie, het is iets dat telbaar is (bijvoorbeeld: we kunnen
drie ruimtelijke dimensies onderscheiden, “drie” is de
intensiteit van “ruimtelijke dimensie” als entiteit, dus als we
van één dimensie naar twee dimensies gaan, verdubbelen we de
intensiteit). We kunnen ons dat voorstellen als een mogelijke
constante (1+k)n’.
De tijd is hierbij een gemakkelijke metafoor voor gebeurtenissen
die elkaar uitsluiten als stappen in een proces en deze metafoor
zullen we nu gebruiken om op een didactische manier het inzicht aan
te brengen (en niet telkens weer te verwijzen naar de meer abstracte
interpretatie).
Hieronder geven we de grafiek die de relatie geeft tussen m, de
intensiteit van de eenheid op de abscis, en n, het aantal
processtappen op de ordinaat, voor twee verschillende positieve k
(vierkant datapunt voor k=0,1 en ruit datapunt voor k=0,3). Het
eerste relevante aantal m is 2, het grootste in deze grafiek is 20.
Dit illustreert duidelijk dat een ver-m-voudiging (bijvoorbeeld een
verdubbeling voor m=2) van een gekozen (x-x0) voor een
grotere eigenwaarde “sneller” bereikt wordt (dus bereikt wordt
binnen een kleiner aantal stappen van het verder niet gespecificeerde
proces).
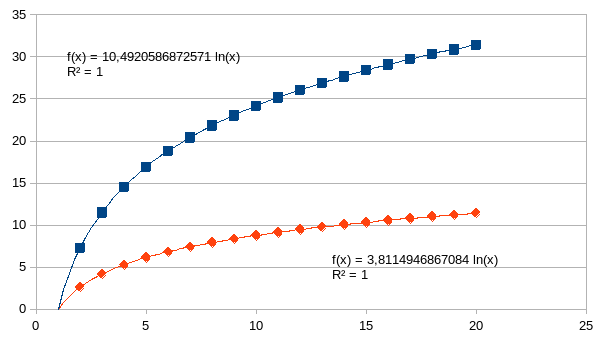
De
m wordt gegeven op de x-as en zoals elke logaritmische curve kunnen
we n uitdrukken als een gewogen natuurlijke logaritme en de
vergelijking is opgenomen als f(x) in de grafiek. De minimale waarde
m, de verdubbeling, geeft dus aan binnen hoeveel stappen n van het
proces een tweede eenheid “ontstaat” naast de waargenomen
eenheid, namelijk het gekozen verschil (x-x0).
Dit is een zeer verhelderende grafiek voor het geval we zouden
vergeten wat we juist hiermee modelleren. De n die gemodelleerd wordt
heeft slechts zijdelings iets met tijd te maken. Het is de minimum
(maximum) intensiteit (“in de tijd” van het proces of “in de
ruimte” van het proces) waarbij een bepaalde soort
uitsluiting optreedt (en dus waarneembaar en dus telbaar wordt als
een aantal). Immers: de invariante entiteit die in een toestand kan
waargenomen worden zal zich op een bepaalde diepte bevinden in de
tralie zodanig dat elke mogelijke atomaire toestand die
entiteit kan realiseren. Zijn er meer mogelijke toestanden dan
zal de entiteit zich metrisch verder bevinden dan het niveau van die
toestanden en dat is afhankelijk van de relevante tralie. Een tralie
met één onderscheiding kan wederzijdse uitsluiting modelleren van
maar twee toestanden, een tralie met twee onderscheidingen kan
wederzijdse uitsluiting modelleren van maximaal vier toestanden, een
tralie met n onderscheidingen kan wederzijdse uitsluiting van
maximaal 2n toestanden uitdrukken. Aangezien entiteiten
atoomburen zijn voor een bepaald onderscheidingen universum, zal het
aantal entiteiten dat een bepaald gedrag vertoont ook deze
distributie volgen. De waarschijnlijkheid
van waarnemen van een soort (dus de waarschijnlijkheid van één
toestand) zal dus gegeven worden door de fractie 2-n.
We kunnen dan onderzoeken welke relaties tussen k en (x-x0)
mogelijk zijn voor dezelfde n. Dat betekent dus dat we een
aantal processtappen doorlopen (en dus een zeker verschil of afstand
in het proces en a fortiori dus een zekere tijd-afstand
(tijdsverschil) of ruimte-afstand (ruimteverschil)) waarbij een
onderscheidingen universum monotoon toeneemt (of afneemt) zodanig
dat er meer (of minder) even niveaus kunnen ontstaan en we gaan
onderzoeken wat de relatie is tussen eigenwaarden en de soort
eenheden die mogelijks kunnen ontstaan als het proces lang genoeg
loopt.
Betekenis van een schaalfactor
1 onderscheiding, 2 atomen
We veronderstellen eerst de meest eenvoudige situatie: er zijn
maar twee elkaar uitsluitende toestanden, er is dus maar één stap.
Dit is de enige tralie waarvan de modellering van gedrag zich bevindt
op centraal niveau. Dan is n in (x-x0)(1±k)n
gelijk aan 1 en de intensiteit is recht evenredig met (x-x0)
of (1±k), en de mogelijke k is dan 1 minder of meer dan de
verhouding van de intensiteit (x-x0)(1±k) met
(x-x0)(1±0). De dubbelgetallen (x-x0) of (1±k)
spelen dezelfde rol. De enige stap die mogelijk is in een tralie met
slechts twee toestanden a en <a> is het product (of ingebed
product, of creatief product niet verschillend van disjunctie enz...)
van beide toestanden en dit heeft de waarde <> (of <<>>)
en dit heeft de karakteristieken van een eenheid die een gedrag
vertoont als intensiteit. Dat is dus de entiteit <<(x-x0)
of (1±k)>> die ervaren is en dan een bepaalde intensiteit
heeft. Er zijn twee toestanden, dus voor positieve feedback (1+k)
komt k overeen met 1 en voor negatieve feedback (1-k) komt k overeen
met 2-1. Dit is niet anders dan de enige mogelijkheden van
waardetoekenning: voor positieve feedback hebben beide toestanden
dezelfde waarde die niet gekend is (allebei ofwel <<>>,
ofwel <>), voor negatieve feedback hebben de toestanden
tegengestelde waarde en dat is niet anders dan ofwel <>, ofwel
<<>>, en tegengestelde waarde hebben is enkel mogelijk
voor twee aspecten. Het meest primitieve ervaren is dus een negatieve
feedback: een waarde toekennen aan een eenheid die een toestand is en
de intensiteit van die toestand staat voor het aantal toestanden met
dezelfde maar ongekende waarde. Dat betekent dus dat er geen
potentiële toestanden moeten verondersteld worden (toestanden zonder
waarde die enkel in een groter universum elkaar kunnen uitsluiten).
We kunnen dit ook als volgt uitdrukken: toestanden met dezelfde
waarde kunnen ons niet verrassen. Kiezen we voor <<>> als
waarde dan sluiten die toestanden elkaar allemaal uit en de ordening
die hen met elkaar verbindt is de ordening van de gehele getallen. Er
kunnen dus zeer veel toestanden zijn of zeer weinig en deze uitspraak
kunnen we variëren door het aantal van de eenheid te variëren (in
plaats van 1 als intensiteit van <<(x-x0) of (1±k)>>
nemen we bijvoorbeeld m als aantal voor de eenheid, of ook 1/m) en
dat functioneert dus als een schaalfactor.
In het bitmodel is m dan het aantal bits met dezelfde waarde. Het
bitmodel
van een toestand is dus bijvoorbeeld «m(hoogbit), m(laagbit)»
met als tweede zicht op hetzelfde «m(laagbit), m(hoogbit)», wat de
verdubbeling illustreert. Het bitmodel van een toestand is dus
bijvoorbeeld ook «(1/4)m(hoogbit), (1/4)m(laagbit)» met als tweede
zicht op hetzelfde «(1/4)(laagbit), (1/4)m(hoogbit)», wat de
halvering illustreert.
Meerdere onderscheidingen
We kunnen nu die ene stap (de waarde van n, die we nu gelijk aan 1
nemen) als een maximum beschouwen en onderzoeken wat de relatie is
tussen (x-x0) en (1±k) voor een vaste n met 0<n<1.
Daartoe beschouwen we het getal (x-x0)(1±k)n
en de variabelen zijn dus (1±k) en (x-x0). Dat zijn drie
aspecten. Dit maakt heel duidelijk dat er een verschil is tussen
beide termen: de exponent n komt slechts bij één van de
producttermen voor. Stel nu dat we (1±k) als variabele kiezen en dus
(x-x0) als constante (het verschil dat een verschil maakt
veranderen we niet) dan kunnen we veronderstellen dat “op een
bepaald moment of positie of mogelijkheid van uitsluiting”,
namelijk n, een “foto” gemaakt wordt van (het spoor van) de
intensiteiten van twee variabelen, namelijk (x-x0)(1±k)n
en (1±k). Noem de constante (x-x0) nu C, noem het getal
(x-x0)(1±k)n nu de variabele z, en noem het
getal (1±k) nu de variabele y, dan zien we het machtsverband z=Cyn.
De intensiteit z is dus recht evenredig met een macht (n met bereik
tussen 0 en 1) van y. De symmetrische situatie is dus het patroon met
een machtsverband y=(z/C)1/n (want wanneer we de vaste n
met 0<n<1 nemen dan geldt dat ∞>1/n>1). Dit maakt
duidelijk dat we onder deze veronderstellingen gelijk welke positieve
waarde voor n kunnen veronderstellen. De positieve waarden van n
kunnen we interpreteren als geanticipeerde monotoon toenemende
processtappen in de toekomst, de duale anticipatie (processtappen in
de “re”constructie van het verleden) wordt gemodelleerd door
negatieve n.
De variabele y (dit is het dubbelgetal (1±k)) kunnen we voor het
gemak ook een eigenwaarde en resolutie noemen met bereik tussen 1 en
2 voor positieve feedback bij variërende n en tussen 1 en 0
voor negatieve feedback bij variërende n.
Hieronder is een voorbeeld gegeven van drie vaste
exponenten n en de keuze C=1. Met vierkant datapunt is n=0,5 wat
betekent dat de abscis de variabele z geeft en de ordinaat de
variabele y, met ruit datapunt is n=1 wat betekent dat er een vrije
keuze is of de abscis de variabele z geeft en de ordinaat de
variabele y of omgekeerd, met driehoek datapunt is n=1,5 wat betekent
dat de abscis de variabele y geeft en de ordinaat de variabele z.
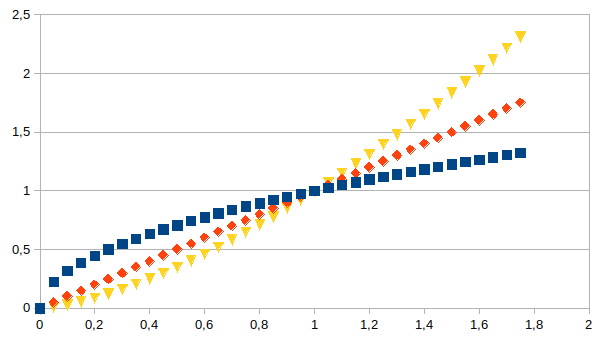
We
hebben de vrije keuze welke variabele we als abscis of ordinaat
kiezen.
We merken nu op dat ook y niet anders is dan een verhouding, een
schaalfactor, een processnelheid.
Dus als we y vermenigvuldigen met een getal (een nieuwe
“schaalfactor”) dan blijft het patroon behouden, het patroon dat
de intensiteit van de verschillende deelaspecten van het totale
proces met elkaar relateert. Immers neem als de schaalfactor de
constante D, verschillend van 1, als een andere factor voor de
resolutie
(1±k), dan is z=C(Dy)n=(CDn)yn. Het
patroon van de verschillende eigenwaarden wordt gewoon met een nieuwe
factor vermenigvuldigd, wat zich uit in een andere lokale helling van
de curve. Hieronder een voorbeeld met een positieve k (dus positieve
feedback bij variërende n) en met n=0,25 constant (niet variërend
dus) en een schaalfactor 1 voor de datapunten met vierkant en 0,5
voor de datapunten met ruit.
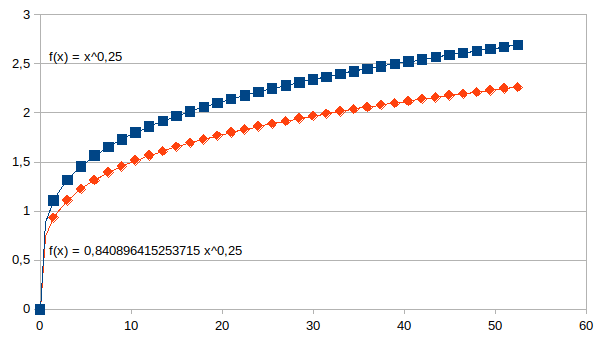
We kunnen z=CDnyn natuurlijk anders
schrijven om meer expliciet naar de
klassieke hypothese te verwijzen:(z/C)1=(y/D-1)n
of dus (z/z0)1=(y/y0)n en
hiermee drukken we twee dimensieloze verhoudingen uit die
expliciet de betrokken eenheden van de klassieke hypothese en,
hierdoor, de schaalfactoren introduceren. Dit kunnen we natuurlijk
ook schrijven als (y/y0)=(z/z0)1/n
als we van een exponent groter dan 1 willen veranderen naar een
exponent kleiner dan 1. Voor anticipaties naar het verleden (die we
“mogelijke reconstructies” noemen) gebruiken we dan een negatieve
n.
Het machtsverband herkennen we ook wanneer we een logaritme nemen:
log(z)-log(z0)=n(log(y)-log(y0)), een lineair
verband, dat we dus zien verschijnen als de eenheden van de assen van
de grafiek logaritmisch verdeeld zijn. Merk op dat y afwijkt van 1,
wat zorgt dat log(y) verschillend is van nul. De verhouding y=(1±k)
kunnen we altijd schrijven als (k0±k0k)/k0
en dus kunnen we altijd een k0 kiezen als de relevante en
waargenomen resolutie.
We kunnen dit als volgt interpreteren: het verband (z/z0)1=(y/y0)n
drukt de voorwaarde uit waaronder het proces met stappen n en
eigenwaarde y waarneembare entiteiten genereert van de soort z0.
Dit betekent ook dat niet alle processen waarneembare entiteiten
genereren. Een waarneembare entiteit wordt discontinu geteld. Een
eenvoudig voorbeeld hiervan wordt geboden door de
Gulden Snede. Er zullen dus ook slechts sommige schaalfactoren y0
zijn die dezelfde entiteiten genereren, en sommige waarneembare
entiteiten zullen slechts na “lang genoeg wachten” ontstaan.
Schaal waarnemen
Twee processen kunnen
interageren. Een typisch voorbeeld hiervan is de “waarneming
door monstername” of “meten van sporen” (dit is een proces a)
van een proces b. Als we het onbekende proces b willen leren kennen,
dan kunnen we dat enkel door een proces a dat we monotoon moeten
laten verlopen. In het tweede proces (b) worden de sporen gegenereerd
die in het eerste proces (a) verzameld worden in categorieën en daar
als entiteiten die elkaar uitsluiten geteld worden. We kunnen altijd
minstens één categorie kiezen. Zelfs al is het onmogelijk om a
priori de relevante categorieën te kennen, toch is altijd een
categorie te maken die alle sporen kan bevatten die niet in de
gekozen categorie(ën) kunnen belanden. Het totaal aantal
monsternames is altijd relevant, hoe meer tijd er is (hoe groter n,
het aantal processtappen van de monstername, namelijk de relevante
elkaar uitsluitende toestanden) hoe meer monsters. Er is minstens ook
altijd één eenheid-met-intensiteit m(x-x0) waarbij de
intensiteiten m geordend kunnen worden want een grotere m impliceert
ook altijd een kleinere m, ook als m niet continu verdeeld is.
Een machtsverband van het type z=Cyn wordt dikwijls
waargenomen bij spontane processen waarbij de deelaspecten yi,
dus eigenwaarden (1±ki), sporen zijn die achtergelaten
worden en dus waargenomen worden.
Al deze machtsverbanden herkennen we nu als effecten die ontstaan
bij de interactie van processen met ofwel een positieve feedback
ofwel een negatieve feedback waarbij de interactie zelf als een som
van feedback processen kan gemodelleerd worden. Essentieel voor een
machtsverband is dat het getal dat tot de macht verheven wordt
verschillend is van 1, en dit is juist wat bereikt wordt met een
1-splitsing: gelijk welke bitstring kan slechts éénmaal op een
willekeurige plaats in twee delen gesplitst worden. We hebben
daarenboven ook aangetoond dat alle bits als verhouding moeten
gemodelleerd worden wanneer men een a priori keuze maakt voor de
grootte van het universum.
Onvermijdelijke schaal
Bij de studie van de schaaleffecten zijn we uitgegaan van een
maximum van één stap (n=1). De veronderstelling dat een verhouding
zinvol is leidt tot de benadering van een minimum van één stap
(1/n=1). Zuiver wiskundig kunnen we dan inzien dat het patroon (de
symmetrie) ook geldt voor een n groter dan 1 en dat dit bereikt wordt
door een verschaling. Dit kunnen we dan niet anders interpreteren dan
dat er meerdere toestanden moeten zijn met dezelfde waarde en dat we
die kunnen afbeelden in een groter universum. Dat betekent dat we dan
uitgaan van een toestand in minimaal een twee onderscheidingen
universum, dat we de tweede stap uitvoeren door een vectorproduct met
een andere toestand en dan als resultaat een atoombuur bereiken, niet
een waarde zoals in het geval van één stap. Veronderstel nu dat we
vertrokken van een AND-atoom dan bereiken we na een eerste stap het
centraal niveau en na een tweede stap genereert dit een OR-atoom. Pas
na de derde stap bereiken we een toestand met waarde. Bij
de eerste stappen die uitsluiting (in meer dan één onderscheiding)
uitdrukken vinden we dan de drie dimensies terug enkel
door betekenis te geven aan schaaleffecten.
Die dimensies kunnen we ook ruimtelijke interpreteren. Dit is
gemakkelijk te illustreren door in de ruimte een lijnstuk, een
vierkant en een kubus met elkaar te vergelijken, met respectievelijke
dimensies 1, 2 en 3. Wanneer we de lengte van een ribbe van de kubus
verdubbelen (factor 21) dan verviervoudigen we een zijde
(factor 22) en verachtvoudigen we het volume (factor 23).
De maximale stap die uitsluiting uitdrukt is hierbij dan 3, de 3
ruimtelijke dimensies, zodat we ook kunnen spreken van fracties van
de maximale eigenwaarde. Dit is hier de driedimensionale ruimte
waarin sporen van processen waargenomen worden. Hierbij is er steeds
een volume betrokken, zelfs als we alleen geïnteresseerd zijn in het
deelaspect “lengte”, of als enkel een lengte kan gemeten of
waargenomen worden. Dus: als we het volume verachtvoudigen, dan
verdubbelen we de lengte, immers 81/3=2 en dus is de
fractie gelijk aan 1/3 voor de lengte, en is de fractie 2/3 voor het
oppervlak en dat geldt voor elke factor f, aangezien f1/3
en f2/3 goed gedefinieerd zijn.
Deze schaal is onvermijdelijk, elke welgevormde haakuitdrukking is
immers als
creatief product in twee onderscheidingen uit te drukken. Elke
entiteit zal dus een volume innemen. Geometrie veronderstellen we
niet in het haakformalisme, we
leiden het af.
Voorbeelden van schaaleffecten
De stijfheid van een ingeklemde balk met rechthoekige doorsnede
onder invloed van een kracht in de richting van de dikte zal altijd
evenredig zijn met de verhouding dikte D tot lengte L tot de derde
macht, dus (D/L)3. Dit is een relatie die gerelateerd is
aan de vorm van de balk. Daardoor zullen niet alle denkbare sporen
van processen waargenomen worden maar zijn ze afhankelijk van de
vorm, die een schaaleffect introduceert. Bijvoorbeeld: de vorm van
grote dieren is niet zomaar een vergrote versie van de vorm van
kleine dieren, de vorm van het dier is geen symmetrie.
Uiteraard kunnen meerdere onderscheidingen een rol spelen en dus
kunnen hogere dimensies bereikt worden en nieuwe symmetrieën
onderscheiden worden in die hogere dimensies. Bijvoorbeeld: het
oppervlaktetraagheidsmoment van een object is eigen aan zijn vorm en
is evenredig met een lineaire maat tot de vierde macht. Vorm
kunnen we modelleren als een structuur, als een organisatie van
posities die leidt tot coördinatie van processen die beperkt worden
door de vorm. Vorm maakt het mogelijk om symmetrie te onderscheiden
en de mechanische symmetrie van het oppervlaktetraagheidsmoment is
inderdaad gerelateerd met deze evenredigheid in de vierde macht.
Deze dimensies kunnen we ons voorstellen als bijkomende relaties
die op elk punt van de onvermijdelijke ruimte-tijd kunnen
onderscheiden worden en die iets kwantificeren van een bijkomende
structuur. Bijvoorbeeld: in dezelfde toestand worden minstens
twee verschillende entiteiten gerealiseerd. Bijvoorbeeld: we kunnen
enkel spreken van “de eigenfrequentie van een fysische trilling”
wanneer voldoende stappen in de tijd onderscheiden kunnen worden, op
een eerder punt van die ordening is van dat aspect geen sprake. Orde
(mogelijkheid tot anticiperen) versus chaos (onmogelijkheid tot
anticiperen) wordt waargenomen als de sporen die zich afscheiden op
verschillende schalen al dan niet anticipeerbaar met elkaar
gerelateerd zijn (door positieve of negatieve feedback) en hierdoor
symmetrieën
ontstaan. Symmetrie is te herkennen wanneer sommige verhoudingen
niet veranderen en dus wanneer sommige onderscheidingen die meetbaar
zijn niet onafhankelijk van elkaar kunnen variëren. Bijvoorbeeld
binnen het ruimte-tijd repertorium: in het gedrag van een fysische
slinger kunnen de periode T en de lengte L niet onafhankelijk van
elkaar veranderd worden, ze zijn gebonden door de verhouding T/√L.
Evenwicht
Eerst veronderstellen we dat het machtsverband kan vastgesteld
worden in een evenwichtssituatie. Evenwichten ontstaan slechts als de
negatieve feedback overheerst voor de invarianten die ontstaan. Een
evenwicht kunnen we bijvoorbeeld niet vanaf de “eerste”
waarnemingen vaststellen, waarbij de invariante aspecten (de eenheden
die waargenomen zouden kunnen worden) nog niet echt duidelijk zijn.
De sporen kunnen wel gebruikt worden voor anticipaties naar het
verleden (die we “mogelijke reconstructies” noemen).
Diffusie
en convectie zijn processen die als het verschil van een
intensiteit tussen twee plaatsen in een driedimensionale ruimte met
een centraal punt kunnen gemodelleerd worden. Dit betekent dat dit
model relevant wordt bij het eerste evenwicht dat mogelijk is bij
veranderende parameters, evenwicht dat slechts mogelijk is vanaf drie
toestanden, het samenspel van dynamiek
in drie dimensies. Elk drievoud van toestanden die dezelfde
waarde hebben modelleert een voorwaarde voor stabiliteit, zoals de
som van drie welgevormde haakuitdrukkingen met dezelfde waarde, som
die onvermijdelijk gelijk is aan nul.
Bijvoorbeeld in het patroon y=Cz1/n: het metabolisme
van een levende entiteit (y1)
is recht evenredig met de lichaamsmassa (z1)
tot de macht ¾ (de wet van Kleiber), en de levensduur ervan (y2)
verschaalt met de lichaamsmassa (z1) tot de macht ¼ . Pas
na een voldoend groot aantal processtappen hebben deze aspecten een
evenwicht bereikt en zijn deze aspecten invariant.
Ook de logaritme herkennen we in de
respons van veel waarnemingsorganen die logaritmisch verandert
met een veranderende intensiteit die waargenomen wordt. Voor sommige
waarnemingen duurt
het een tijd voor een evenwicht bereikt wordt.
Distributie van entiteiten
Als er geen evenwicht situatie bereikt wordt, dan zullen we op een
bepaald moment moeten stoppen met het verzamelen van waarnemingen,
dus we hebben een “vaste n” bereikt, een aantal stappen. Dus de
“vaste n” maakt het mogelijk om te onderzoeken welke entiteiten
(x-x0), gerelateerd met hun intensiteit m, in het vizier
komen. We stoppen het gedrag, de dynamiek, de tijd en kijken naar de
diffusie of convectie op een bepaald moment in de toestandsruimte
waarin we geïnteresseerd zijn met behulp van de verzamelde sporen.
Hoeveel van de veronderstelde entiteiten (categorieën) vinden we
dan?
Wanneer we nu het aantal sporen uitzetten per categorie
construeren we een histogram, een kwantitatieve verdeling of
distributie over de categorieën. Wanneer de categorieën
onafhankelijk van elkaar gegenereerd worden door het repetitief
doorlopen van een proces dan vindt men typisch een Gauss curve.
Telkens weer wordt het proces met dezelfde onderscheidingen
doorlopen. Wanneer de categorieën ontstaan zijn als gevolg van het
vinden van sporen die aspecten zijn binnen één lopend proces dan
vindt men typisch een machtsverband. Er zijn al veel voorbeelden van
machtsverbanden bekend.
Een voorbeeld van een Gauss verdeling is de lengte van volwassen
mensen. De lengte ontstaat als gevolg van een proces dat op een
bepaald ogenblik een evenwicht bereikt. Hoe lang we daarna ook zouden
wachten, na een bepaalde leeftijd worden mensen niet groter. Voor de
lengte kunnen we verschillende categorieën onderscheiden en de
aantallen in die categorieën verschillen van elkaar, maar dat
verschil is beperkt en wordt goed beschreven door de spreiding van de
verdeling. We vinden mensen met lengte van het gemiddelde plus of min
drie maal de spreiding, maar geen mensen met lengte van het
gemiddelde plus of min (bijvoorbeeld) tien maal de spreiding.
Een voorbeeld van een machtsverband is de intensiteit van
aardbevingen. Het proces van wrijving van tektonische platen kan
energie bufferen tot een bepaald moment. Dan genereert dit schokken
en schokken genereren andere schokken en dit is een proces met een
zekere ver-m-voudiging. Het proces blijft lopen, we weten niet of we
de grootst mogelijke schokken al gehad hebben en we nemen voortdurend
kleine schokken waar. Evenwicht wordt niet bereikt. Aardbevingen
worden ondergebracht in categorieën waarmee we aan elke aardbeving
een soort toekennen. De soorten zijn de intensiteiten van schokken.
Een grotere schok impliceert een kleinere schok en er is een grootste
schok te vinden in de verzamelde sporen. We kunnen van een gemiddelde
schok spreken in een bepaalde regio maar dat zegt helemaal niets over
de grootte van mogelijke schokken in die regio. Typisch zijn schokken
exponentieel groter (of kleiner) en wijken niet zo maar een fractie
af van het gemiddelde. Gelijk welke klok kunnen we gebruiken om de
aardbevingen te ordenen in een bepaalde regio, zo komen we tot een
frequentie van aardbevingen (z). Het blijkt dat dit evenredig is met
hun intensiteit (y) (de soort aardbeving) tot de macht -1. Hier zien
we een negatieve macht. De processtappen kunnen we negatief kiezen om
processen in het verleden te modelleren waarvan we voldoende stabiele
sporen kunnen terugvinden. Ook voor distributies geldt dat er
voldoende waarnemingen moeten mogelijk zijn omdat dan pas de eenheden
duidelijk zijn die waargenomen zouden kunnen worden (voor
aardbevingen hebben we ooit moeten beslissen welke schokken nu nog
relevant zijn en hoe ze zouden gemeten worden, en het interpreteren
van mogelijke sporen van aardbevingen in het verre verleden in de
bestaande categorieën is al helemaal moeilijk, denk aan de impact
die we moeten veronderstellen van een asteroïde 66 miljoen jaar
geleden, impact die verbonden wordt met het verdwijnen van de laatste
niet vliegende dinosauriërs).
Het is opvallend dat de distributie z=Cy-1 (die we
kunnen vaststellen bij aardbevingen) voor andere processen
veralgemeend kan worden tot z=Cy-n, maar dat we dikwijls
vinden dat de schaal parameter n begrensd is: 2<n<3.
Het is opvallend dat voor veel distributies de machtsverbanden
voornamelijk in de “staart” van de grafiek waargenomen worden,
wat betekent dat een machtsverband slechts gevonden wordt eens een
bepaalde waarde overschreden wordt. Dit is uiteraard een gevolg van
het feit dat een onderscheidingen universum groot genoeg moet zijn om
nieuwe vormen van coördinatie
mogelijk te maken (en dus om nieuwe entiteiten te kunnen
onderscheiden).
De verschillende distributies kunnen we daarom verklaren
binnen de structuur van een tralie.
Besluit
Entiteiten zijn op verschillende schalen waar te nemen, te meten
en dus te beschrijven en sommige schalen zijn aan elkaar gerelateerd
als ze aspecten zijn van eenzelfde proces. “Dezelfde” entiteit
kan zich dan anders voordoen, waarbij elke schaal sommige
onderscheidingen naar voor brengt die op een andere schaal
niet kunnen onderscheiden worden of, anders gezegd, niet binnen de
waarnemingsresolutie vallen, of die expliciet niet beschouwd worden.
Schaal is een noodzakelijk begrip om gedrag te beschrijven en
impliceert dus elkaar uitsluitende aspecten van dat gedrag. Iets
anders kunnen we niet tellen en tellen gebeurt altijd discontinu.
Interagerende entiteiten “vertonen emergent gedrag”, gedrag dat
enkel op het niveau van de interactie of de “coördinatie van de
entiteiten” kan beschreven worden. Door coördinatie ontstaat orde.
Dat is dus gedrag “op een grotere schaal”, er zijn meer
entiteiten en meer interacties mogelijk. Dat gedrag kan spontaan zijn
(“zelforganiserend”) en kan ook patronen vertonen die dan enkel
in een groter universum te beschrijven zijn. De patronen worden dan
beschreven in een universum waarin de individuele entiteiten niet
relevant zijn. Dus een gedrag dat kan vertoond worden door levenloze
entiteiten kan ook vertoond worden door levende cellen en hele
maatschappijen.


