De axioma's van de waarschijnlijkheidsrekening (Kolmogorov) hebben we kunnen afleiden uit het ene axioma van het haakformalisme. We hebben hiervoor de relatie van relevantie gebruikt die op zijn beurt afgeleid werd uit het ene axioma. De relatie van relevantie geeft een relatie tussen gecollapste tralies en een gecollapste tralie moeten we ons voorstellen als het resterende potentiële deel van een tralie waar twee punten een waarde toegekend kregen (de ene niet te onderscheiden van <>, de andere niet te onderscheiden van <<>>). De waarschijnlijkheidsrekening is dus ontwikkeld om kwantitatieve relaties in kaart te brengen tussen gecollapste tralies, de aard van de signatuur van de bits speelt hierbij helemaal geen rol.

We merken nu op dat in de waarschijnlijkheidsrekening het axioma moet aangenomen worden dat XOR niet kan onderscheiden worden van OR (met uiteraard het duaal dat de transformatie niet kan onderscheiden worden van de conjunctie). Het meest voor de hand liggende voorbeeld wordt dan gegeven door de atomen. En inderdaad het is volkomen irrelevant of we nu AND-atomen of OR-atomen beschouwen, min signatuur of plus signatuur. We merken nu op dat er punten zijn binnen een tralie waarvoor evenzeer geldt dat de vectorvermenigvuldiging en de disjunctie niet van elkaar onderscheiden zijn en we hebben deze gelokaliseerd bij het onderzoek naar het waarnemen van nieuwe aspecten. Ook voor deze punten zullen we een maat kunnen definiëren die, binnen de veronderstelling dat de tralie op een bepaalde manier collapst, voldoet aan het derde axioma van de waarschijnlijkheidsrekening.

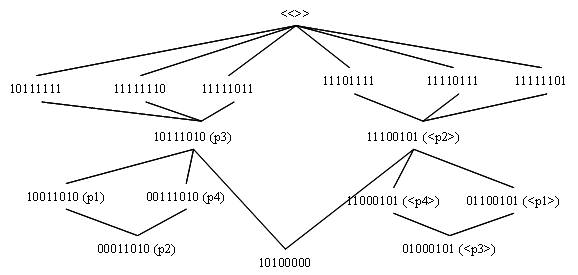
Om de aandacht te richten gebruiken we het voorbeeld waarmee we het haakbitmodel in functie van de M symbolen uitgewerkt hebben. In de onderstaande deeltralie is een splitsing gemaakt van punten die door de componenten van de waarnemingscontext gerealiseerd worden.

Het punt dat waargenomen wordt, is M•M^<>, als haakbitmodel 10100000, bij de waarneming zelf kan het niet onderscheiden worden van <>, in bitmodel x0x00000.

De twee componenten van de meetcontext worden gegeven door M, als haakbitmodel 10111010, en M^<>, als haakbitmodel 11100101. In het ervaren (bij de collaps waarbij M•M^<> niet kan onderscheiden worden van <>, en enkel bij de collaps) geldt dat M•M^<>=M⊕M^<>, of dus x0x00000 = x0xxx0x0 ⊕ xxx00x0x. Merk op (rekenen met gecollapste haakvectoren) dat dan de disjunctie MM^<>=10100000, het niet gecollapste infimum.

We gaan dus uit van de hypothese: er zijn p (een aantal) atomen die een bedoelde meetbare eigenschap van de entiteit realiseren en er zijn p^<> (een aantal) atomen die iets anders dan de bedoelde meetbare eigenschap van de entiteit realiseren. We gaan uit van de veronderstelling dat de aantallen verwijzen naar de aantallen atomen binnen één tralie die door die atomen opgespannen wordt. Deze uitspraak in de standaard taal heeft zijn duaal in het gebeuren.

De atomen zijn gekarakteriseerd doordat alle bits identiek zijn behalve 1. Ze sluiten elkaar uit dus bij elke realisatie van de meetcontext wordt er één gerealiseerd (duaal: gebeurt er één). Het is die éne bit, die zich dus telkens op een andere positie bevindt, die dus geteld wordt in het aantal. Het totaal aantal bits dat hierbij betrokken is, is een deel van een groter aantal n waarvan een aantal m gemeenschappelijk zijn en dus karakteristiek zijn voor de atomen die we in dezelfde categorie onderbrengen (meetcontext M of meetcontext M^<>). Beide componenten van de meetcontext worden gerealiseerd door elkaar uitsluitende vluchtige atomen die, als ze ervaren zijn een van de componenten van de meetcontext realiseren en waarbij simultaan iets anders gebeurt. De aantallen n en m zijn niet gekend en we zullen aantonen dat ze wel achteraf kunnen gekozen worden uitgaande van de telling van atomen. Er geldt in deze hypothese dus: n = m+p+p^<>.

Noteer: twee bitstrings van n bits hebben altijd m gemeenschappelijke bits en p verschillende bits. Zowel de m als de p kunnen in twee categorieën onderverdeeld worden: de hoogbits en de laagbits. Er geldt: m_h+m_l+p_h+p_l=n. De twee strings onderscheiden zich doordat de p_h van de ene de p_l van de andere is en omgekeerd. We vereenvoudigen de m_h+m_l tot m_h zonder daarmee aan algemeenheid in te boeten, wat we daarmee wel doen is kiezen voor <> als referentiepunt.

We beschouwen nu een potentieel punt dat waargenomen kan worden in een meetcontext. In het waarnemen zal het punt de ervaringswaarde "ervaren" krijgen en dus niet kunnen onderscheiden worden van <> (namelijk ...000000...).

Het totaal aantal bits dat we nodig hebben om het universum voor te stellen is n. Het punt (de entiteit die we gaan waarnemen) stellen we voor door (m1)0000000... waarmee we aanduiden dat het op een metrisch niveau m boven <> ligt. We hebben immers aangetoond dat het niveauverschil een metrische maat is. Is het punt ervaren dan stellen we dit voor als (mx)0000000... waarbij de x voor don't cares staan. Merk op dat de volgorde van de bits niet belangrijk is, en door een geschikte transformatie in de volgorde kunnen gebracht worden waarin ze hier voorgesteld worden.

Het infimum van de ene meetcontext (neem dit als M^<> ) is (m1)(p1)0000000... Dit infimum realiseert het punt M•M^<>en dit infimum wordt gerealiseerd door het aantal p^<> = n-m-p atomen, dat is dus het aantal nulbits in dit punt.

Het infimum van de andere meetcontext is (m1)(p0)111111111... Dit infimum realiseert het punt M•M^<>en dit infimum wordt gerealiseerd door het aantal p atomen, dat is dus het aantal nulbits in dit punt.

M en M^<> sluiten elkaar uit. De twee infima zijn dus gekarakteriseerd doordat ze elkaars inbedding zijn op de m identieke éénbits na. We moeten blijven beseffen dat deze keuze voor nulbits of eenbits toevallig is, dus de laatste zin moeten we ook in een meer abstracte betekenis toelaten: de twee infima zijn gekarakteriseerd doordat ze elkaars inbedding zijn op de m identieke bits na (welke waarde die ook zouden hebben). In de berekeningen die we zullen maken zullen we trouwens alleen de begrippen “identieke bits” en “verschillende bits” nodig hebben. In concrete voorbeelden (die een niet te versmaden leidraad blijven) zullen we onvermijdelijk een keuze moeten maken voor welke bits dit zijn, en we proberen die keuze zo eenvoudig mogelijk te houden.

Als we de metingen uitvoeren dan zijn er twee aantallen gemeten: het aantal atomen dat M realiseert (p) en het aantal atomen dat M^<> realiseert (n-m-p = p^<>). De som van het aantal atomen dat M^<> (of (m1)(p1)00000...) realiseert en dat M (of (m1)(p0)11111...) realiseert is n-m. Noch n, noch m zijn op voorhand gekend, maar kunnen vrij gekozen worden, ermee rekening houdend dat n-m het totaal aantal is van de waarnemingen, dus n-m=p+p^<>. De vrije keuze is de uitdrukking van de symmetrie die waargenomen wordt: de invariant 10100000 in beide meetcontexten, invariant voor de conjunctie operatie.