In het haakbitmodel kunnen we de waarnemingscontext waarin nieuwe aspecten optreden uitdrukken als 10100000BITXOR10111010BITXNOR11100101. (Noteer dat BITXOR staat voor de haak-XNOR en de BITXNOR staat voor de haak-XOR).

We merken op dat het infimum van de triade (10100000; 10111010; 11100101) die zo gevormd is, dus 10100000, zowel de OR als de XOR is van beide andere punten. Wanneer 10100000 niet verschillend is van 00000000, dan krijgen we de triade (x0x00000; x0x11010; x1x00101). We voeren hiermee een collaps uit zodanig dat de twee punten langs de rechtse kant van de triade de inbedding zijn van elkaar. Zoals elke collaps genereert dit een inwendige involutie. Het meest linkse punt van de triade kan dan niet onderscheiden worden van het ervaren zelf en we merken op dat in het ervaren van de drie punten geldt dat x0x00000 = x0xxx0x0 ⊕ xxx00x0x. Hierin gebruiken we het symbool = voor BITXOR en het symbool ⊕ voor BITXNOR. In het ervaren zelf krijgt het symbool = dus een vectorgelijkheid als betekenis en het symbool ⊕ een vectorsom. We zouden deze collaps kunnen voorstellen door een index c bij de voorstelling als M symbolen, en bijvoorbeeld de collaps van M noteren als (M)_c en dan wordt x0x00000 = x0xxx0x0 ⊕ xxx00x0x genoteerd als (M)_c•(M^<>)_c=(M•M^<>)_c=(M)_c⊕(M^<>)_c.

Merk op dat, als een van beide rechtse termen van de triade (10100000; 10111010; 11100101) ervaren is, 10100000 simultaan ervaren is. De beide rechter termen zijn echter niet simultaan te ervaren: de AND van beide rechter termen is 11111111. Een vluchtig atoom is bijvoorbeeld 11111011, het is ruimer dan 10100000, het is ruimer dan 10111010 maar het is niet ruimer dan 11100101, het sluit dit laatste punt uit. Dit staat ons toe te zeggen dat in de beschouwde vluchtige toestand 11111011 de entiteit 10100000 de eigenschap 10111010 heeft. Dit is een waargenomen of gemeten eigenschap, tijdens de meting dus, een dynamische toestand die maar even stabiel blijft (namelijk in 10111111, 11111011 en 11111110) en andere uitsluit. Dit is exact zo, juist door de eigenschap van XOR. We merken nu op dat de partiële ordening van de tralie ook de meting van een partiële orde met zich meebrengt. 11111011 realiseert niet alleen simultaan 11111011 en 10111010 maar ook de tussenliggende 10111011 en 11111010.

De haakbits zijn voor mensen iets gemakkelijker te volgen dan de haakvorm en deze vorm kan gemakkelijk gebruikt worden om een ordinale meting te expliciteren. Omdat dit de meest compacte voorstellingsvorm is, zullen we de structuur van de waarnemingscontext in deze vorm verder expliciteren.

De toegevoegde onderscheiding

Zoals er verschillende kandidaten zijn voor een atoom dat M realiseert, zo zijn er ook verschillende kandidaten voor een creatief toegevoegd aspect. We noteren een creatief product als (x⊗y)_a∼<a<x>><<a><y>>. Dit is dus een disjunctie van <a<x>> en <<a><y>>, beide elementen zijn een conjunctie van twee termen, een term op basis van het toegevoegd aspect en een andere term. Dus <a<x>> is <a>ANDx en <<a><y>> is aANDy, en dus is (x⊗y)_a∼<a<x>><<a><y>> te schrijven als (<a>ANDx)OR(aANDy). De bitgewijze logica van het binair isomorfisme van welgevormde haakuitdrukkingen laat nu toe te onderzoeken welke mogelijke kandidaten er zijn voor de invulling van a als we als x en y M en M^<> nemen. In de onderstaande tabel staat een punt voor de vrije keuze van bit.

Dit maakt duidelijk dat er 2² mogelijkheden zijn voor een toegevoegde welgevormde haakuitdrukking. Bij nauwkeurige analyse zien we dat de vier mogelijkheden zich tot M en M^<> verhouden zoals aangegeven in de onderstaande deeltralie waarin daarenboven ook een duidelijke splitsing gemaakt van punten die door de componenten van de waarnemingscontext gerealiseerd worden.

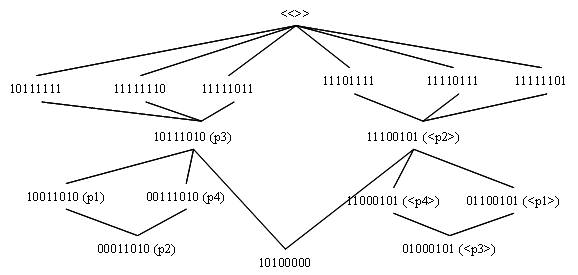
We herinneren eraan dat we de uiterste beschouwde toestanden (AND atomen) hier wel in bitstring noteren maar dat deze toestanden niet stabiel zijn: ze zijn er enkel in het ervaren, momenteel dus en zijn niet simultaan te ervaren. Uiteraard geven deze toestanden aanleiding tot stabiele (gemeten, waargenomen) eigenschappen, die dus fijner zijn dan deze toestanden.

Er zijn vier punten fijner dan 10111010 (inclusief dus 10111010): p₁, p₂, p₃, p₄

Er zijn vier punten fijner dan 11100101 (inclusief dus 11100101). <p₁>, <p₂>, <p₃>, <p₄>

Die punten zijn elkaar inbedding. Wanneer een punt fijner is dan 10111010, dan is de inbedding van het punt fijner dan 11100101.

Deze punten kunnen in het algemeen als volgt geconstrueerd worden: waar in de linkerlid component van de triade (10100000; 10111010; 11100101) een 0 staat, staat in de andere componenten in de ene term een 1 en in de andere term een 0, dus dit voldoet al aan de voorwaarde van inbedding. Waar in het linkerlid van de triade (10100000; 10111010; 11100101) een 1 staat, staat in de andere componenten een 1, één hiervan moet een nul worden om te voldoen aan inbedding EN om een fijner punt te geven dat kans maakt om het bedoelde punt p (of <p>) te zijn. Er zijn twee bits 1 in het linkerlid, dus er zijn vier mogelijkheden

p₁ = 10011010

<p₁> = 01100101

p₂ = 00011010

<p₂> = 11100101

p₃ = 10111010

<p₃> = 01000101

p₄ = 00111010

<p₄> = 11000101

Deze punten worden door de toestanden van de meetcontext gerealiseerd maar ook door de meetcontext zelf en aangezien ze simultaan zijn met de meetcontext zullen we ze interpreteren als eigenschappen van de meetmethode. Merk op dat ze een tralie vormen, dus er is een supremum p₃ dat de andere impliceert met p₂ het infimum van de ene tralie, en er is een infimum <p₃> dat door de andere infima geïmpliceerd wordt met <p₂> als supremum van de andere tralie. De punten p₃ en <p₂> zijn de componenten van de waarnemingscontext, dus M en M<>: een waarnemingscontext realiseert simultaan de meetmethode (de ene deeltralie fijner dan p₃, versus de andere deeltralie fijner dan <p₂> zowel als de gemeten entiteit 10100000. De infima van de tralie zullen we de meetmiddelen noemen, ze zijn p₂ en <p₃>, dus <M> en <M^<>>. Dat niet elk punt mogelijk is maakt duidelijk dat niet elk meetmiddel mogelijk is, toegepast kan worden om een eigenschap van de entiteit te meten.

De infima van de totale tralie zijn dus de gemeten entiteit 10100000 en twee meetmiddelen <M> en <M^<>>.

Meetmiddelen voldoen dan aan de volgende eisen:

00011010OR01000101 is 00000000 en 00011010AND01000101 is 01011111 en is dus iets anders dan 10100000, de gemeten entiteit.

Meetmiddelen: 00011010XOR01000101 is 10100000, de waargenomen entiteit.

Waarnemingscontext: 10111010XOR11100101 is 10100000, de waargenomen entiteit.

We kunnen nog andere eigenschappen van de tralie afleiden. Wat we meten is 10100000, dit is de OR van 10111010 en 11100101, de meetcontext. De meetcontext componenten zijn een AND van punten die elkaars inbedding zijn. Dus: p₁ANDp₄OR<p₁>AND<p₄> is 10100000. In haaknotering herkennen we <<p₁><p₄>><p₁p₄> en dit is <p₁•p₄> maar ook het anti commutatief creatief product (<p₄>⊗p₄)_p1∼(<p₁>⊗p₁)_p4. Zowel p₁ als p₄ kunnen dus als toegevoegde onderscheiding of spoor van de interactie begrepen worden.

In het algemeen kunnen we dus de tralie van de kwantum hypothese voorstellen door het supremum <<>>, het ene meetmiddel M als de nevenschikking A_i, (met een A_k als een AND-atoom) en het andere meetmiddel M^<> als A_j, waarbij noch i noch j op voorhand gekend zijn en verschillend kunnen zijn van elkaar en de meetcontext de nevenschikking A_iA_j is. Bij al deze nevenschikkingen is er geen verschil met het vectorproduct.

Het onderzoek naar de structuur van een meetmethode kan er toe leiden dat men de positie van M en M^<> kan wijzigen. Dit betekent dus dat de meetmethode de 1 bits moet hebben die in de onderzochte toestand ook aanwezig zijn. Anderzijds: de kwaliteit van de meetmiddelen hangt af van de 0 bits die dezelfde waarde moeten hebben. Het supremum van een waarnemingscontext is altijd <<>>, het infimum van een waarnemingscontext is altijd het waar te nemen punt.