In de klassieke hypothese beschouwen we bekende entiteiten. Ze zijn duidelijk gedefinieerd aan de hand van hun opbouwende onderscheidingen. In de tijd veranderen ze (al dan niet waarneembaar) en vertonen ze dus een gedrag. Daarbij wordt de laatst toegevoegde onderscheiding niet ingebouwd en kan alleen maar een momentane intensiteit uniek coderen. Onderscheidingen die tijdens de meting gegenereerd worden, worden niet in staat geacht de entiteit te veranderen, zijn voor de gemeten entiteit irrelevant, zijn enkel relevant voor het gedrag van de entiteit. De klassieke hypothese kijkt dus niet dieper dan atomen en atoomburen en we kunnen dus de andersduale patroon notatie inzetten.

Als we dan iets kunnen tellen dan nemen we de intensiteit van de entiteit <x_i><<x>_i> waar en ervaren we dus de entiteit. Er zijn dus slechts twee AND-atomen ruimer dan <x_i><<x>_i>: <x_i> en <<x>_i>. Deze beide atomen in het hoogste universum zijn door contradualeren in elkaar om te zetten (dit is een gevolg van de mogelijkheid om iets te tellen), ze zijn dus elkaars toegevoegden. En aangezien het AND-atomen zijn, zijn ze niet simultaan te realiseren. Hun conjunctie heeft een waarde: <<>>. In het ervaren zelf zijn ze niet te onderscheiden van <> en het is ofwel het punt <x_i> ofwel het punt <<x>_i> dat ervaren wordt. Een ervaren <x_i> kan genoteerd worden als de klassieke vector <<>>⊕x_i en een ervaren <<x>_i> kan genoteerd worden als de klassieke vector <<>>⊕<x>_i.

Schematisch als tralie voorgesteld bekijken we dus de situatie:

Deze tralie heeft één punt met een waarde en drie punten zonder waarde. Inderdaad: merk op dat <x_i<x>_i>↔<<>> altijd geldt maar dat <x_i><<x>_i> nog geen waarde kan toegekend worden. Het is een uitdrukking die zegt dat de onderscheidingen dezelfde waarde hebben, wat die ook moge zijn. We geven een waarde op moment dat we beslissen en dus waarnemen. In de meting is dan ofwel <x_i> ofwel <<x>_i> ervaren, we zeggen “ja” tegen ofwel <x_i> ofwel <<x>_i>, en dus hoe dan ook zeggen we “ja” tegen <x_i><<x>_i>, <x_i><<x>_i> is ervaren simultaan met het ervaren van een van de atomen en het is onmogelijk om twee atomen simultaan waar te nemen. Om die “ja” te kunnen zeggen moeten we “ja” ofwel “neen” zeggen over de aanwezigheid van elke individuele onderscheiding (dit is juist de eigenschap van een atoom en de uitdrukking van de volledige kennis die we veronderstellen te hebben over de klassieke entiteit die dan waargenomen wordt). De klassieke hypothese legt dus het relevante universum van een entiteit vast.

We hebben onderzocht hoeveel entiteiten in één tralie kunnen voorgesteld worden. Dit maakt duidelijk dat dit mogelijk is op alle even niveaus. Alle even niveaus zijn daarenboven als atoomburen te beschouwen van een niveau dat alleen maar in het hoogste universum weer te geven is.

Naarmate i toeneemt, en dus het aantal opbouwende onderscheidingen van de entiteit <x_i><<x>_i>, liggen de niveaus waarop de andersduale punten zich bevinden verder uiteen (de metrische afstand, gemeten als niveauverschil, tussen bijvoorbeeld <x₄><<x>₄> en <x₅><<x>₅> is groter dan tussen bijvoorbeeld <x₃><<x>₃> en <x₄><<x>₄>). Die tussenliggende niveaus worden door de klassieke hypothese niet gemodelleerd (maar wel door de kwantum hypothese). Bij de stap naar de atoombuur verliezen alle tralies 1 onderscheiding, maar dan worden grotere stappen genomen om een volgende onderscheiding te verliezen. Dit is wat we bedoelen als we zeggen dat de klassieke hypothese uitgaat van een gekende entiteit: één getal i ligt vast juist omdat we dat kiezen, andere onderscheidingen doen zich voor als “laatst toegevoegd” op het moment zelf. Immers: de beide atomen worden bereikt door een AND van onderscheidingen die de entiteit "momentaan karakteriseren" met de laatst toegevoegde onderscheiding, onderscheiding die niet ingebouwd wordt en dus de entiteit niet blijvend karakteriseert, waarbij elke onderscheiding als laatste zou kunnen functioneren. Merk op dat juist dit uitgedrukt wordt door de patroon notatie van een atoombuur. Dit is het eenvoudigst in te zien met een voorbeeld in het drie onderscheidingen universum. De atoombuur <x_i><<x>_i> is daar voor te stellen als <abc><<a><b><c>>, en dit is de welgevormde haakuitdrukking die overeenkomt met elk van de volgende creatieve producten: (<bc>⊗<<b><c>>)_a of (<ac>⊗<<a><c>>)_b of (<ab>⊗<<a><b>>)_c of (<<b><c>>⊗<bc>)_<a> of (<<a><c>>⊗<ac>)_<b> of (<<a><b>>⊗<ab>)_<c>. Men hoeft hierin geen keuze te maken, elke onderscheiding en elke inbedding van een onderscheiding kunnen we beschouwen als de laatst toegevoegde. De twee termen van het creatief product zijn elkaars contraduaal.

Dit levert ons een tweede model op van de klassieke hypothese: de twee atomen zijn dus enerzijds een AND van de andere onderscheidingen met ℵ en anderzijds een AND van de andere onderscheidingen met <ℵ>, waarbij dus elke onderscheiding de rol van ℵ kan opnemen. Elke individuele onderscheiding x (of <x>) kan dus als laatst toegevoegde onderscheiding ℵ beschouwd worden. We kunnen dit ook noteren als <ℵ<p>> versus <<ℵ><q>>.

Schematisch als tralie voorgesteld bekijken we dus de situatie:

Hierbij is duidelijk dat ook p en q aan elkaar gerelateerd zijn, en wel als volgt: stel dat geldt dat <ℵ<p>>↔<x_i>, dan geldt dat <<ℵ><q>>↔<<x>_i>. Een patroon vorm is dan ook dat het ene atoom dan voorgesteld wordt door <ℵx_i >, het andere atoom door <<ℵ><x>_i>. Dit model beklemtoont de pijl van de tijd en toont dat de associativiteit die door de laatst toegevoegde onderscheiding geïntroduceerd wordt het begrip “invers” of “verhouding” zinvol maakt.

De tijd kan gemodelleerd worden door de laatst toegevoegde onderscheiding die de basis is die ervoor zorgt dat de termen van het creatief product zich als getallen gedragen. Inderdaad, de drie haakuitdrukkingen zonder waarde zijn als volgt te schrijven in de basis van ℵ:

<ℵ<p>>∼<>⊕ℵ⊕<p>⊕<ℵ•p>∼p•(<>⊕<ℵ>)⊕<<>>•(<>⊕ℵ)∼(p⊗<<>>)_ℵ

<<ℵ><q>>∼<>⊕<ℵ>⊕<q>⊕ℵ•q∼<<>>•(<>⊕<ℵ>)⊕q•(<>⊕ℵ)∼(<<>>⊗q)_ℵ

<ℵ<p>><<ℵ><q>>∼<p>⊕<q>⊕<ℵ•p>⊕ℵ•q∼p•(<>⊕<ℵ>)⊕q•(<>⊕ℵ)∼(p⊗q)_ℵ

De termen van het creatief product gedragen zich dus als getallen en een invers is gedefinieerd ten opzichte van <<>>, dus stel dat we p voorstellen door <x_i-1> dan moeten we q voorstellen door <<x>_i-1>. Dit is dus de modellering in het haakformalisme van de klassieke getallen g versus g^-1.

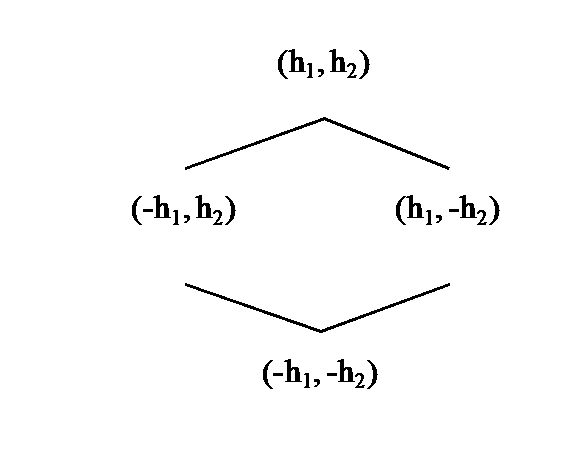
We kunnen deze beide modellen als een speciaal geval van nog een derde model representeren: de klassieke hypothese komt overeen met het opsplitsen van een ongekend lange bitstring in twee ongekend lange bitstrings door één symmetrische beslissing. Dit kan slechts éénmaal, door slechts één keuze. Die ene keuze genereert twee strings die beide “even ongekend” lang zijn en in het geval van de klassieke hypothese elkaars contraduaal zijn. Die éne splitsing in een ongekend universum hebben we eveneens als ℵ voorgesteld. Die zeer abstracte ℵ is de enige onderscheiding waarmee een potentiële tralie kan opgebouwd worden: de tralie van het 1 splitsing universum, met onbekenden h₁ en h₂ die we als componenten van een array afbeelden (een geordend koppel). Die tralie zal met één beslissing om een van de atomen te ervaren collapsen naar een tralie met supremum <<>>, en infimum <>.

Of

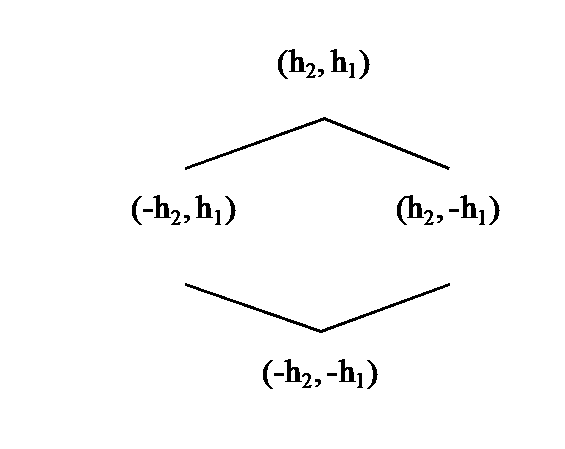
Aangezien beide deel strings ongekend lang kunnen zijn, zijn dat dus twee zichten op dezelfde string.

De klassieke hypothese kan altijd gemaakt worden en is het a priori dat er telbare entiteiten zijn, focuspunten van aandacht die zich niet onderscheiden van elkaar, behalve één aspect dat gebruikt wordt om ze te kunnen tellen. De andere aspecten hebben dezelfde ervaringswaarde, wat die ook moge zijn, zijn aspecten van wat geteld wordt en zijn dus niet dat éne aspect dat gebruikt wordt voor het tellen. Dit neemt niet weg dat men ook in de klassieke hypothese kan spreken van deelentiteiten en dat men altijd kan proberen om hun relaties op een logische manier te beschrijven en men altijd kan proberen andere aspecten te tellen. Maar de entiteit zal altijd ook nog anders zijn dan die beschrijving.