Creatief product
Graaf eerste alternatief
Graaf tweede alternatief
(h•x⊗h•y)h•g
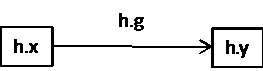
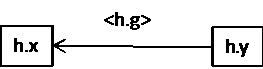
(h•x⊗h•y)<h•g>
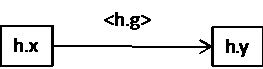
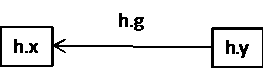
Het creatief product kunnen we voorstellen als gerichte graaf waarbij de twee termen van het product de labeling van de knooppunten zijn en de toegevoegde welgevormde haakuitdrukking de labeling van de boog tussen beide.
In zijn algemene vorm is het creatief product in functie van zijn welgevormde haakuitdrukkingen en vanuit het standpunt h te schrijven als (h•x⊗h•y)h•g en in de vorm van een vector som is dit <h•x>⊕<h•y>⊕<g•x>⊕g•y. Het is vooral de eerste vorm die rechtstreeks als graaf kan geïnterpreteerd worden. In de tabel geven we de vertaling van dat niet-commutatief product en de overeenkomstige gerichte graaf.
Creatief product |
Graaf eerste alternatief |
Graaf tweede alternatief |
(h•x⊗h•y)h•g |
|
|
(h•x⊗h•y)<h•g> |
|
|
Op basis van deze meest eenvoudige graaf kunnen dan multi-grafen gebouwd worden die modelleren hoe verschillende onderscheidingen universa in elkaar zouden kunnen transformeren.
Het creatief product is associatief wanneer dezelfde toegevoegde onderscheiding gebruikt wordt. Dat betekent dus dat hiermee een graaf met meerdere nodes kan voorgesteld worden waar de bogen allemaal dezelfde betekenis hebben. Een toepassing hiervan is de category theory waarin knooppunten en bogen objecten en pijlen genoemd worden. De category theory vereist het aanvaarden van het axioma van associativiteit, wat het haakformalisme niet vereist.
Het creatief product is commutatief wanneer beide termen van het product niet kunnen onderscheiden worden. Dit modelleert dan een boog die als een lus voorgesteld wordt van het knooppunt met zichzelf.
Een gerichte graaf waarin er geen verschil gemaakt wordt tussen knooppunten en bogen (nodes en edges) stelt dan een logische binaire relatie voor, bijvoorbeeld voor de conjunctie <<a><b>> is dit bijvoorbeeld het creatief product (b⊗a)b.