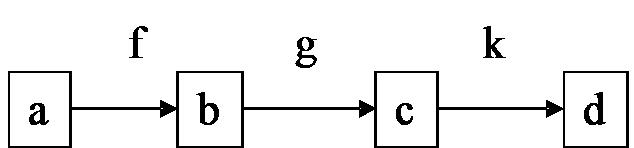De categorietheorie is wellicht de meest succesvolle alternatieve benadering van de verzamelingen theorie als basis voor de wiskunde. We tonen aan dat de axioma’s van de categorietheorie overkoepeld worden door het ene axioma van het haakformalisme, en hoe de categorietheorie vanuit het ene axioma (<> versus <<>>) kan geconstrueerd worden door toepassing van het creatief product.

Axioma's van de categorietheorie

We herinneren eerst de axioma's van de categorietheorie geformuleerd door een van de grondleggers ervan: Saunders Mac Lane. De zo gedefinieerde categorieën noemt Saunders Mac Lane meta-categorieën omdat ze enkel op axioma’s gebaseerd zijn en niet op de verzamelingen theorie. De categorie theorie heeft als primitieven “objecten” (of focus punten zonder dat iets gekend is over hun “inwendige structuur”) en “pijlen” (relaties tussen focus punten). Een categorie is dan een interpretatie van die axioma's in de verzamelingen theorie.

Het is de bedoeling om de onderliggende veronderstellingen uit die axioma’s bloot te leggen in de taal van en met behulp van het haakformalisme.

Een metagraf heeft objecten a, b, c, … en pijlen f, g, h, …en twee operaties: domein en codomein. Een definitie van objecten, pijlen of operaties wordt niet gegeven. Domein wijst aan elke pijl f een object a toe ook geschreven als DOM_f (bron van de pijl). Codomein wijst aan elke pijl f een object b toe ook geschreven als COD_f (doel van de pijl). Een metacategorie is een metagraf met nog twee operaties: identiteit die aan elk object a een pijl ID_a toewijst, ook als 1_a geschreven, en compositie die aan elk paar pijlen (g, f) met DOM_g = COD_f een pijl toewijst g*f van DOM_f naar COD_g.

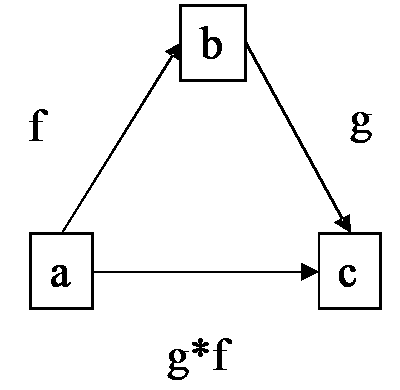
Een belangrijk inzicht dat door de categorietheorie aangebracht wordt is dat de pijlen en de objecten exact dezelfde rol spelen. Er zijn dus in het bovenstaande schema drie objecten: a, b en c en ook drie pijlen f, g en g*f. Ze definiëren elkaar op een unieke manier en het is enkel onze grafische voorstelling die zes symbolen nodig heeft: a, b, c, f, g en * en daardoor dus zeer redundant is. Anders gezegd: als we b nu g zouden noemen en c nu g*f zouden noemen dan moeten we a nu f noemen.

De axioma's van de categorietheorie zijn nu associativiteit en eenheid.

Associativiteit

Het axioma van associativiteit in de categorie theorie zegt dat k*(g*f) = (k*g)*f in de volgende metagraf altijd geldt

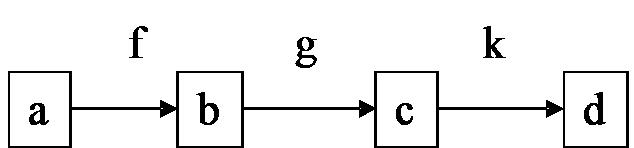
Dit wordt door het volgende “commuterende” diagram uitgedrukt:

Eenheid

Het axioma van eenheid zegt dat voor alle pijlen f van a naar b en g van b naar c de samenstelling met de eenheidspijl 1_b met linkse en rechtse vermenigvuldiging gegeven wordt door

1_b*f = f

g*1_b = g

Dit wordt door het volgende commuterende diagram uitgedrukt:

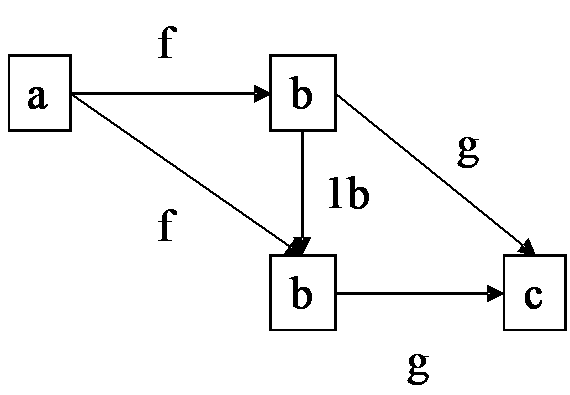
De vertaling in het haakformalisme

Objecten, pijlen (morfismen), operaties van toewijzing van domeinen en codomeinen aan morfismen worden in het haakformalisme voorgesteld door één en hetzelfde begrip: een welgevormde haakuitdrukking voorgesteld met behulp van het creatief product. De samenstelling van pijlen is het creatief product van het creatief product, bijvoorbeeld is de samenstelling f*g met een toegevoegde onderscheiding u de welgevormde haakuitdrukking <u<f>><<u><g>>, anders te noteren als (f⊗g)_u. Hierbij moeten we dus opmerken dat f, g en u welgevormde haakuitdrukkingen zijn die als creatief product geschreven worden.

Associativiteit

De toegevoegde onderscheiding u kunnen we in het haakformalisme ook begrijpen door die te beschouwen als de “laatst toegevoegde onderscheiding” ℵ die drie vormen kan aannemen:

1. een welgevormde haakuitdrukking uit het opgespannen universum en die het opgespannen universum dus reduceert (convergentie)

2. een welgevormde haakuitdrukking die geen deel gaat uitmaken van het opgespannen universum en dus vluchtig is (stabiliteit)

3. een nieuwe welgevormde haakuitdrukking die het opgespannen universum dus uitbreidt (divergentie)

We bewijzen dat enkel het creatief product met één welbepaalde toegevoegde onderscheiding associatief is, van welk type dat ook zou zijn. We hebben dus bewezen dat dan geldt dat (f*g)*h en f*(g*h) niet te onderscheiden zijn.

In het haakformalisme kunnen we daarenboven de associativiteit van het creatief product ook in een groter geheel kenmerken waarin het geven van een waarde aan een transformatie (dus u↔v↔ℵ) een essentiële rol speelt. Dat is dus “op het moment” dat men een creatief product van creatieve producten construeert met behulp van welgevormde haakuitdrukkingen die dezelfde waarde hebben. Hiermee tonen we ook concreet aan hoe de categorietheorie ontstaat uit het haakformalisme door die voorwaarde toe te voegen. Het is dus niet nodig de eis van associativiteit op een andere manier in het haakformalisme in te voeren.

Noteer dat het creatief product niet commutatief is, (f⊗g)_ℵ is verschillend van (g⊗f)_ℵ.

Eenheid

De veronderstelling van de categorietheorie is dat de compositie met de eenheid (ofwel links ofwel rechts) de transformatie niet verandert, op een zodanige manier dat de compositie van transformaties evenmin verandert.

Dus 1_a*f = f en g*1_a = g moeten ervoor zorgen dat g*1_a*1_a*f = g*f. Door de associativiteit speelt 1_a*1_a een centrale rol, dit is in welgevormde haakuitdrukking <ℵ<a>><<ℵ><a>> en dit is niet te onderscheiden van a, wat a ook moge zijn, bijvoorbeeld ook een projector of een willekeurige som van twee welgevormde haakuitdrukkingen. Dus g*1_a*f = g*f veronderstelt dat 1_a gegeven wordt door (a⊗a)_ℵ, f gegeven wordt door (a⊗b)_ℵ en g gegeven wordt door (c⊗a)_ℵ. Dat de centrale uitdrukking (hier dus 1_a) in het resultaat geen rol meer speelt is een rechtstreeks gevolg van de introductie van associativiteit in het haakformalisme. Merk op dat we helemaal geen veronderstelling gemaakt hebben over a, het is een willekeurige welgevormde haakuitdrukking.

We merken nu ook op dat de eis van associativiteit voor sommige gevallen van de compositie van de operatie * een transformatie maakt. We kunnen nu onderzoeken wat de gevolgen zijn van het nemen van de eenheid van transformatie (namelijk <>) als de eenheid van compositie met *. Volledig duaal zouden we de eenheid van vectorproduct (namelijk <<>>) als de eenheid van compositie met * kunnen nemen. We zullen daartoe de composities expliciet berekenen in het haakformalisme waardoor de onderliggende veronderstelling duidelijk wordt die het mogelijk maakt het gelijkheidsteken te gebruiken:

f als <>*f is <u<<>>><<u><f>> is dus niet verschillend van <u>f

g als g*<> is <u<g>><<u><<>>> is dus niet verschillend van ug

g*f is dus <u<ug>><<u><<u>f>> en dit is dus niet verschillend van <u<g>><<u><f>> en dit is niet verschillend van de definitie van deze operatie.

We kunnen nu het axioma van de eenheidstransformatie uit de categorietheorie nu nog duidelijker begrijpen in de taal van het haakformalisme. We merken op dat de linkse compositie van de eenheidstransformatie met f als resultaat <u>f geeft, en niet f. Wanneer <u>f niet kan onderscheiden worden van f hebben we dus een collaps uitgevoerd, namelijk f↔<u>f, of volledig equivalent <<f<<u>f>><<f><u>f>>↔<> en dus <<uf><<>>>↔<> dus uf↔<>. Dit is een nevenschikking en dus geen vectorproduct. De samenstelling van f met een eenheidsmorfisme zorgt dus voor een keuzevrijheid uf in een groter universum, keuzevrijheid die niet meer kan onderscheiden worden van <>, de eenheidstransformatie. Het uitvoeren van de substitutie van f door <u>f betekent dat uf ervaren wordt. Dit is een infimum dat collapst. Als we f ervaren, ervaren we uf, als we u ervaren, ervaren we uf maar ook: uf is ervaren zonder dat f ervaren is of u ervaren is. Maar dit betekent ook dat er twee andere punten zijn die elkaars inbedding zijn en die zich gedragen als de klassieke hypothese. Dit hebben we immers expliciet uitgewerkt met een voorbeeld: ca is dit voorbeeld het infimum van <<a><c<b>>> en <a<c>><<a><b>c> en dit is ervaren als <<a><c<b>>> en <a<c>><<a><b>c> elkaars inbedding zijn en dus XOR niet verschillend is van OR. Vervang c door u en a door f en de twee punten die elkaars inbedding zijn zijn geconstrueerd.

Volledig analoog geldt deze redenering voor de rechtse compositie met de eenheidstransformatie.

Gevolg: het axioma van de eenheidstransformatie uit de categorietheorie hoeft in het haakformalisme niet geïntroduceerd te worden omdat het er terug op neerkomt dat een waarde gegeven wordt aan een transformatie (in dit geval dus f↔<u>f, of dus uf↔<>, met als concreet voorbeeld <<f><u<b>>>•<f<u>><<f><b>u>↔<>) en niet anders is dan het basisaxioma van het haakformalisme: een agens ervaart iets als het iets anders laat gebeuren. Dit leidt tot twee categorieën die elkaar uitsluiten. Dit maakt duidelijk dat in de categorietheorie bijkomende veronderstellingen gemaakt moeten worden die in het haakformalisme uit een fundamentelere benadering kunnen afgeleid worden.

Bespreking van enkele concepten uit de categorie theorie

Domein en codomein

De categorietheorie moet een onderscheid maken tussen het domein van een morfisme en zijn codomein. Dit is enkel nodig bij de samenstelling van morfismen.

In het haakformalisme kunnen dit ook als volgt uitdrukken: als we een ongekende f en ongekende g willen samenbrengen in een groter universum dan kunnen we het punt dat daar voor zorgt expliciet construeren als een f_k die tot het f_i universum behoort, maar ook als een g_l die tot het g_j universum behoort. Dat gemeenschappelijk punt kunnen we een unieke naam geven en noemen we u. Het punt dat we bereiken in het samengestelde universum is dan <u<f_i>><<u><g_j>>. Dit is een OR van <u<f_i>> en <<u><g_j>>die niet verschillend is van een XOR aangezien de AND van beide niet kan onderscheiden worden van <<>>.

De uitspraak “De compositie van beide transformaties is slechts mogelijk als COD_f en DOM_g overeenkomen” betekent dus dat de relatie van inbedding impliciet gebruikt wordt in de categorietheorie (in dit geval u versus <u>). Inderdaad: de categorietheorie kent het dualiteitsprincipe dat ook in het haakformalisme gekend is.

De begrippen domein en codomein zijn enkel zinvol bij asymmetrisch gebruik (gerichte morfismen), dus bij gebruik van het creatief product. De categorietheorie veronderstelt dus impliciet een geordende opbouw van een universum door toevoeging van onderscheidingen. Dit is de betekenis van domein en codomein: willen f en g kunnen samengesteld worden tot een morfisme, dus een transformatie in één universum, dan moeten ze creatief opgebouwd worden vanuit <> en <<>>, op een zodanige manier dat er een aspect u gemeenschappelijk kan gevonden worden, waarbij uf collapst naar <> wanneer <u>g collapst naar <>.

Inderdaad <u<f>><<u><g>> kunnen we ook schrijven als <<uf><<u>g>> en dit is ervaren wanneer zowel uf collapst naar <> als <u>g collapst naar <>.

Als we ons nu afvragen wat het domein van g is (voor de combinatie met f) dan is <u> een goede kandidaat op voorwaarde dat u het codomein is van f (voor de combinatie met g). Merk op dat dit allemaal relatieve uitspraken zijn. Merk op dat uf↔<u>f niet te onderscheiden is van f, evenmin als ug↔<u>g niet te onderscheiden is van g.

Bewijs: we drukken uf↔<u>f uit in welgevormde haakuitdrukking, en reduceren:

<<uf<<u>f>><<uf><u>f>>

<<uf><<u>f>>

f<<u><<u>>>

f

QED

Inverteerbaar morfisme

Een transformatie e van a naar b is inverteerbaar indien er een transformatie e' bestaat van b naar a waarbij e'*e=1_a en e*e'=1_b. Men spreekt van een links invers en een rechts invers.

In het haakformalisme is dat onmiddellijk duidelijk vanuit de twee eenheden die impliciet in het associatief creatief product geïmpliceerd worden.

Veronderstel nu dat er geen verschil is tussen 1_a en 1_b aangezien a<> noch b<> kunnen onderscheiden worden van <>.

e'*e=1_a is

<r<e'>><<r><e>>

e*e'=1_b.

<s<e>><<s><e'>>

e'*e=1_a AND e*e'=1_b is dus

<<<r<e'>><<r><e>>><<s<e>><<s><e'>>>>

Deze uitdrukking is in onder de volgende voorwaarden niet verschillend van <>:

r↔<s> AND e'↔<e> AND s↔<e>

<<<r<e'>><<r><e>>><<s<e>><<s><e'>>>>

<<<<s>e><s<e>>><<<e><e>><ee>>>

<<<ee><<e><e>>><e<e>>>

<<<e>e><e<e>>>

<<<>><<>>>

<>

AND impliceert XNOR, dus wat zeker voldoet is ook <r>↔e'↔<e>↔s en dit is een even transformatie.

Bewijs: we substitueren in <<<r<e'>><<r><e>>><<s<e>><<s><e'>>>> voor één van de symbolen, neem bijvoorbeeld s:

<<<<s><s>><ss>><<ss><<s><s>>>>

<<<<s>><s>><<s><<s>>>>

<<s<s>><<s>s>>

<>

Wat betekent dat? Voor e_i en e'_j als “deelverzamelingen” moeten supremum en infimum zich niet onderscheiden van elkaar.

We onderscheiden monomorfisme en epimorfisme.

Monomorfisme

Het morfisme f is een monomorfisme indien f*g₁=f*g₂ impliceert dat g₁=g₂ voor gelijk welke g_i.

We vertalen, en drukken uit dat g₁en g₂ hetzelfde domein/codomein paar hebben:

<u<f>><<u><g₁>>

<u<f>><<u><g₂>>

Gelijkheid

<<<u<f>><<u><g₁>><<u<f>><<u><g₂>>>><<<u<f>><<u><g₁>>><u<f>><<u><g₂>>>>

<<<u<f>><<u><g₁>><u><g₂>><<u><g₁><u<f>><<u><g₂>>>>

<<g₁<u><g₂>><<u><g₁>g₂>>

<u><<g₁<g₂>><<g₁>g₂>>

In deze welgevormde uitdrukking komt f niet meer voor, dus “f kan geschrapt worden”. Deze uitdrukking impliceert <<g₁<g₂>><<g₁>g₂>> in het geval dat

<<u><<g₁<g₂>><<g₁>g₂>>><<g₁<g₂>><<g₁>g₂>> of dus

<<u>><<g₁<g₂>><<g₁>g₂>>

Dus: <u> is ruimer dan de transformatie g₁↔g₂ bijvoorbeeld ruimer dan <<g₁><g₂>>. In een formaat dat domein en codomein aanduidt geldt dus de transformatie <<g₁<g₂>><<g₁>g₂>>↔<u><<g₁<g₂>><<g₁>g₂>>

Een transformatie met een links invers is een monomorfisme.

Epimorfisme

Het morfisme f is een epimorfisme indien g₁*f=g₂*f impliceert dat g₁=g₂ voor gelijk welke g_i.

We vertalen:

<u<g₁>><<u><f>>

<u<g₂>><<u><f>>

Gelijkheid

<<<u<g₁>><<u><f>><<u<g₂>><<u><f>>>><<<u<g₁>><<u><f>>><u<g₂>><<u><f>>>>

<<g₁u<g₂>><u<g₁>g₂>>

u<<g₁<g₂>><<g₁>g₂>>

Dit impliceert <<g₁<g₂>><<g₁>g₂>> in het geval dat

<u<<g₁<g₂>><<g₁>g₂>>><<g₁<g₂>><<g₁>g₂>> of dus

<u><<g₁<g₂>><<g₁>g₂>>

Dus: u is ruimer dan de transformatie g₁↔g₂ bijvoorbeeld ruimer dan <<g₁><g₂>>. In een formaat dat domein en codomein aanduidt geldt dus de transformatie <<g₁<g₂>><<g₁>g₂>>↔u<<g₁<g₂>><<g₁>g₂>>

Een transformatie met een rechts invers is een epimorfisme.

Verschil tussen monomorfisme en epimorfisme

Het verschil tussen monomorfisme en epimorfisme is het verschil tussen een keuzevrijheid, meerdere punten dus, die een transformatie impliceren of een ingebedde keuzevrijheid, één punt dus, die een transformatie impliceert.

De behandeling met morfismen is wel algemeen geldend maar de atomen van een universum komen ermee weinig tot hun recht.

In die zin zijn monomorfisme en epimorfisme wel te begrijpen als opsplitsingen in de repertoria in de tabel, waarbij dus<<g₁<g₂>><<g₁>g₂>> de rol speelt van y_j (elk punt kan altijd als een transformatie uitgedrukt worden).

Speciaal geval

Het speciaal geval (f⊗g)_f is fANDg en dit is niet verschillend van (g⊗f)_g. Dit is dus wel commutatief en associatief.

Wanneer is <u<f>><<u><g>> niet verschillend van <<f><g>>.

<<<u<f>><<u><g>><f><g>><<<u<f>><<u><g>>><<f><g>>>>

<<<<u<f>><<u><g>>><<f><g>>>>

<<<<u<f><<f><g>>><<u><g><<f><g>>>>>>

<<u<f>g><<u><g>f>>

Er zijn nu drie mogelijkheden tussen twee van de drie welgevormde haakuitdrukkingen die deze uitdrukking de waarde <> geven

1. <u>↔g: inderdaad: <<<g><f>g><g<g>f>>↔<<<><f>><<>f>>↔<>

2. g↔f: inderdaad: <<u<f>f><<u><f>f>>↔<<u<>><<u><>>↔<>

3. u↔f: inderdaad: <<f<f>g><<f><g>f>>↔<<<>g><<><g>>>↔<>

Deze voorwaarden zijn identiek met de voorwaarde voor het bestaan van een invers.

Dus bij klassieke inverteerbare substituties met telbare variabelen is de samenstelling van morfismen een AND.

Noteer:

De AND van <u<f>><<u><g>> en <<f<g>><<f>g>> is <<f><g>>.

<<<u<f>><<u><g>>><f<g>><<f>g>>

<<<u<f><f<g>><<f>g>><<u><g><f<g>><<f>g>>>>

<<<u<f><g>><<u><g><f>>>>

<<f><g><<u><<u>>>>

<<f><g>>

Discrete categorie

Een categorie is discreet wanneer elke transformatie de identiteit is, dus ervaren is. Elke verzameling is een verzameling van zo'n objecten: <>f_i. Een monoid heeft één object, en wordt door de verzameling van al zijn transformaties en de identiteitstransformatie gekenmerkt. Dus <> is een monoid.