We construeren een 1-splitsing met intervallen als termen ((ni-nj)⊗(ni+nj))ℵ. De intervallen worden geconstrueerd als een som of verschil van gehele getallen en in de interpretatie van het haakformalisme zijn getallen aantallen onderscheidingen. (ni-nj) modelleert een eenheid met een richting en dus ook een zin, in het haakformalisme is dat een gecollapste haakuitdrukking, bijvoorbeeld (y⊕<x>). (ni+nj) modelleert een eenheid die alleen maar kan toenemen, of duaal, alleen maar kan afnemen, bijvoorbeeld de welgevormde haakuitdrukking h in een onderscheidingen universum van onbekende grootte met een laatst toegevoegde onderscheiding ℵ. Een som van welgevormde haakuitdrukkingen is altijd een gecollapste haakuitdrukking, tenzij in het 3&1 patroon, vandaar dat we (ni+nj) interpreteren als een welgevormde haakuitdrukking. Als haakuitdrukking is een interval in het algemeen geval een gecollapste haakuitdrukking, een haakuitdrukking met don’t cares, en modelleert dus het vectorproduct van een welgevormde haakuitdrukking met een ervaren haakuitdrukking.
Met die intervallen berekenen we een schaalfactor vij als een verhouding van die aantallen vij=(ni-nj)/(ni+nj). Een verhouding (ni-nj)/(ni+nj) is altijd als een product te schrijven. Verschillende schaalfactoren zijn met elkaar gerelateerd als ze een procesevenwicht kunnen modelleren. Dit procesevenwicht is niet anders dan de uitdrukking dat een som van schaalfactoren gelijk is aan nul, bijvoorbeeld vij+vjk+vki=0. Met de verschillen wordt dus een nul geconstrueerd en dit drukt een evenwicht uit, een situatie waarin er geen verandering meer waargenomen wordt (de verandering is zeer klein en onwaarneembaar kleiner). vij+vjk+vki=0 schrijven we ook als vij+vjk=vik en deze som kunnen we interpreteren als een Lorentz boost en we ontwikkelen een meer abstracte versie van de Lorentz transformatie die de relatie geeft tussen de termen (ni-nj) en (ni+nj).
Een speciaal en belangrijke veronderstelling is dat een van de vij gelijk is aan nul. Hieruit volgt dat we eigenlijk een puntsnelheid veronderstellen (wat we goed in het oog moeten houden omdat we snelheid begrijpen als een verschil tussen twee toestanden). We hebben dat grondig onderzocht en kwamen dan tot de conclusie dat dit enerzijds “een rekenkundig gemiddelde tijd” veronderstelt maar anderzijds dat ook het verband tussen de toestanden verloren gaat. De reeks metingen n0; n1; n2; n3; n4; n5; n6… van de veronderstelde toestanden T0; T1; T2; T3; T4; T5; T6… worden enkel gebruikt voor een constructie ten opzichte van steeds dezelfde waarde ½. Dus men veronderstelt (ni-½)/(ni+½), een “lokaal evenwicht ni” dat gevolgd kan worden door een willekeurige andere intensiteit (nj-½)/(nj+½) van een toestand die de eerste uitsluit en een nieuw lokaal evenwicht weergeeft dat niet gerelateerd is aan het “lokaal evenwicht ni”.
Relaties die een uitdrukking zijn van evenwicht veranderen niet als hetzelfde interval I bij alle intervallen bijgeteld wordt die de gesloten lus vormen. Aan I worden geen eisen gesteld, dit is het eenvoudigst in te zien in het binair model van een evenwicht: de som van drie bits (eenheden van een ervaren toestand) met dezelfde waarde is nul. De intervallen zijn dus invariant voor die Lorentz transformatie. De interpretatie is dan dat die bepaalde keuze een standpunt modelleert van waaruit de relatie waargenomen wordt. Dat geldt dus voor de getallen ni waarmee de verhoudingen berekend worden. Dat betekent in de interpretatie van het haakformalisme dat er altijd toestanden en dus onderscheidingen toe te voegen zijn die dezelfde waarde hebben en dus geen verschil maken dat een verschil maakt. Inderdaad, door de verschillen “snelheid” en “versnelling” te modelleren, modelleren we enkel kwantitatieve aspecten van ervaren toestanden die gegenereerd worden door een laatst toegevoegde onderscheiding ((ni-nj)⊗(ni+nj))ℵ. In de klassieke hypothese kunnen we niet doordringen in de structuur van de entiteiten die een gedrag vertonen, de entiteiten zijn datgene dat geen verschil maakt. Dat interval I dat we kunnen veronderstellen bij alle verschillen die samen een evenwicht kunnen uitdrukken, zullen we “een Lorentz invariant” noemen omdat we zullen aantonen dat dit een verdere abstractie is van het gekende begrip.
Het is verhelderend om eens expliciet aan te tonen hoe een verhouding verandert door het interval I toe te voegen omdat de noemers van de verhoudingen wel degelijk veranderen door toevoeging van een getal m aan elk getal ni, waarbij m ook gelijk kan zijn aan nul. We gaan hier dan ook een nieuwe notatie bij nodig hebben die reflecteert dat we bij elk getal ni eenzelfde getal m bijtellen.
In plaats van v01=(n0-n1)/(n0+n1) beschouwen we nu v01+m=(m+n0-m-n1)/(m+n0+m+n1)=(n0-n1)/(2m+n0+n1). Hier is enkel de noemer afhankelijk van m.
We berekenen nu 1+vij+m=1+(ni-nj)/(2m+ni+nj)={(2m+ni+nj)+(ni-nj)}/(2m+ni+nj)=(2m+2ni)/(2m+ni+nj) en hierbij zijn zowel teller als noemer afhankelijk van m.
We berekenen het kwadraat van de verhouding: v2ij+m=(ni-nj)2/(2m+ni+nj)2 en dus 1-v2ij+m=(2m+ni+nj)2/(2m+ni+nj)2-(ni-nj)2/(2m+ni+nj)2=((2m+ni+nj)2-(ni-nj)2)/(2m+ni+nj)2=((2m+ni+nj)+(ni-nj))((2m+ni+nj)-(ni-nj))/(2m+ni+nj)2=((2m+2ni)((2m+2nj))/(2m+ni+nj)2=4(m+ni)(m+nj)/(2m+ni+nj)2
We berekenen nu t01+m+v12+mx01+m
(2m+n0+n1)+(n1-n2)(n0-n1)/(2m+n1+n2)
{(2m+n0+n1)(2m+n1+n2)+(n1-n2)(n0-n1)}/(2m+n1+n2)
(4m2+2mn1+2mn2+2mn0+n0n1+n0n2+2mn1+n12+n1n2+n1n0-n12-n0n2+n1n2)/(2m+n1+n2)
((4m2+2mn0+2mn2)+2n1(2m+n0+n2))/(2m+n1+n2)
(2m(2m+n0+n2)+2n1(2m+n0+n2))/(2m+n1+n2)
Dus t01+m+v12+mx01+m=(2m+2n1)(2m+n0+n2)/(2m+n1+n2)∼t02+m.
We stellen 1/γ12+m=(2m+2n1)/(2m+n1+n2)
Dus er geldt dat:
t02+m=γ12+m(t01+m+v12+mx01+m).
We berekenen nu x01+m+v12+mt01+m
(n0-n1)+(n1-n2)(2m+n0+n1)/(2m+n1+n2)
{(n0-n1)(2m+n1+n2)+(n1-n2)(2m+n0+n1)}/(2m+n1+n2)
(2m+2n1)(n0-n2)/(2m+n1+n2)
Hier vinden we ook dezelfde factor 1/γ12+m=(2m+2n1)/(2m+n1+n2).
Dus er geldt dat:
x02+m=γ12+m(x01+m+v12+mt01+m).
Volledig gelijkaardig kunnen we dat berekenen voor de factor 1/γ21+m en vaststellen dat:
1/γ12+mγ21+m=((2m+2n1)/(2m+n1+n2))((2m+2n2)/(2m+n1+n2))
1/γ12+mγ21+m=4(m+n1)(m+n2)/(2m+n1+n2)2=1-v212+m
We kunnen dus stellen dat τ212+m=4(m+n1)(m+n2) en t212+m=(2m+n1+n2)2
We kunnen nu berekenen wat de som van verhoudingen wordt (de Lorentz boost). Deze is (v01+m+v12+m)(1+v01+mv12+m)-1.
Teller: (v01+m+v12+m)=(n0-n1)/(2m+n0+n1)+(n1-n2)/(2m+n1+n2)=((2m+n1+n2)(n0-n1)+(2m+n0+n1)(n1-n2))/(2m+n0+n1)(2m+n1+n2)
Noemer: (1+v01+mv12+m)=((2m+n0+n1)(2m+n1+n2)+(n0-n1)(n1-n2))/(2m+n0+n1)(2m+n1+n2)
(v01+m+v12+m)(1+v01+mv12+m)-1=((2m+n1+n2)(n0-n1)+(2m+n0+n1)(n1-n2))/((2m+n0+n1)(2m+n1+n2)+(n0-n1)(n1-n2))=
(2mn0+2n0n1-2n1n0-2mn2)/(2m(2m+n0+n2)+2n1(2m+n0+n2))=
2(m+n1)(n0-n2)/2(m+n1)(2m+n0+n2)=
(n0-n2)/(2m+n0+n2)=v02+m
Dus v02+m=(v01+m+v12+m)(1+v01+mv12+m)-1 en de relatie van een Lorentz boost is dus onveranderd.
We berekenen eerst het verschil van twee op elkaar volgende schaalfactoren, verhoudingen of snelheden v01+m en v12+m omdat een versnelling enkel op die manier kan gedefinieerd worden. Het verschil is:
(v01+m-v12+m)=(n0-n1)/(2m+n0+n1)-(n1-n2)/(2m+n1+n2)=
((2m+n1+n2)(n0-n1)-(2m+n0+n1)(n1-n2))/(2m+n0+n1)(2m+n1+n2)=
(2m(n0-2n1+n2)+2n0n2-2n12)/(2m+n0+n1)(2m+n1+n2)
De versnelling wordt gemodelleerd door het kwadrateren van de noemer.
De versnelling is dus (2m(n0-2n1+n2)+2n0n2-2n12)/(2m+n0+n1)2(2m+n1+n2)2.
De versnelling is dus een som van twee componenten, een met een teller afhankelijk van m, namelijk 2m(n0-2n1+n2)/(2m+n0+n1)2(2m+n1+n2)2 en een met een teller die niet afhankelijk is van m, namelijk (2n0n2-2n12)/(2m+n0+n1)2(2m+n1+n2)2.
De teller van de versnelling is (2m(n0-2n1+n2)+2n0n2-2n12) en bekijken we nu als een vierkantsvergelijking in n1. Als alle ni dezelfde waarde hebben dan is deze nul. Maar deze is ook nul in twee andere gevallen: de nulpunten van de vierkantsvergelijking -2n12-4mn1+2m(n0+n2)+2n0n2 of dus 2n12+4mn1-2m(n0+n2)-2n0n2
De determinant van deze vierkantsvergelijking is 16m2+16(mn0+mn2+n0n2), de wortel hieruit is 4(m2+mn0+mn2+n0n2)1/2. Dit is niet anders dan 4(m+n0)1/2(m+n2)1/2.
De nulpunten van de vierkantsvergelijking zijn dus:
n1=-m+(m2+mn0+mn2+n0n2)1/2
n1=-m-(m2+mn0+mn2+n0n2)1/2
(m2+mn0+mn2+n0n2)=(m+n0)(m+n2) is terug een vierkantsvergelijking, maar nu in m, en die is nul voor m2+m(n0+n2)+n0n2=0. De determinant is dus (n0-n2)2 en dus altijd positief. Dit is een parabool met symmetrie as m=-½(n0+n2).
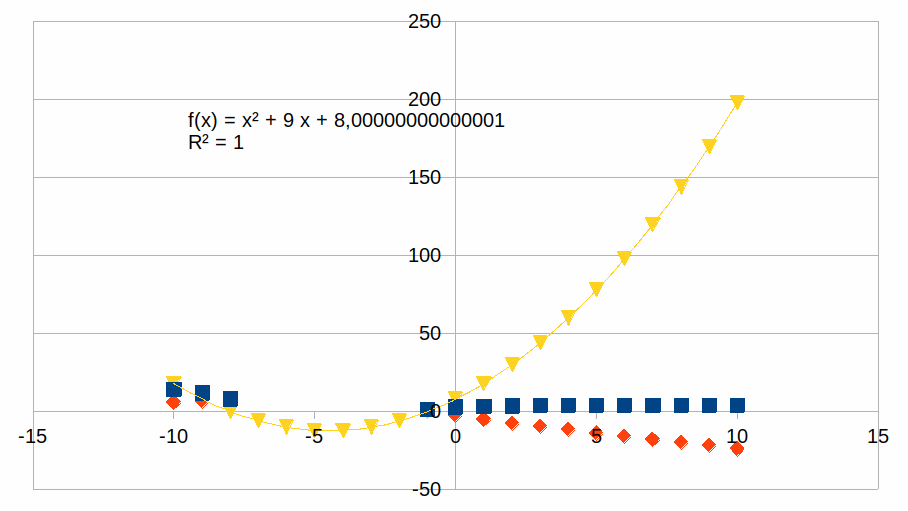
Hieronder een voorbeeld om de aandacht te richten met n0=1 en n2=8. In dezelfde grafiek zijn ook de twee mogelijkheden voor n1 aangegeven (respectievelijk vierkant datapunt en ruit datapunt). Het ontbrekende deel in beide reeksen datapunten maakt duidelijk dat n1 daar een complex getal is (dubbelgetal) en dat is wanneer de determinant (de parabool) negatieve waarden aanneemt.

Een m is altijd te veronderstellen, ook als getal. Wat de waarde ook is van m, de relaties in een evenwicht situatie blijven dezelfde en we vinden de oorspronkelijke relaties terug voor m=0. Dit noemen we het Lorentz nulpunt. Dus m is een modellering voor het aantal toestanden die een verschil maken dat geen verschil maakt, in het ervaren hebben ze allemaal dezelfde waarde. Aangezien het toestanden zijn kan die waarde alleen maar <<>> zijn (of “neen”, of “niet te kiezen”). Dit noemen we het Lorentz interval. Er is verder ook niets verondersteld over m, m kan dus evenzeer een structuur zijn (bijvoorbeeld een complex getal), m kan positief zijn of negatief. Bij de schaalfactor vij+m komt de m niet voor in de teller maar wel in de noemer. De schaalfactor verandert dus wel degelijk en een andere m verandert de noemer van de verhouding, de term die enkel kan toenemen en in het getallendomein kunnen we dat interpreteren als de eenheid die een intensiteit (de teller) heeft. Men kan zich dus inbeelden dat dit modelleert dat de keuze voor een willekeurig startpunt voor de intensiteit die alleen maar kan toenemen (en daardoor geordend is) een aantal processen zal selecteren waarin een procesevenwicht mogelijk is (m heeft dan een waarde verschillend van nul en alle interagerende processen hebben dezelfde m), terwijl er processen zijn die voor dat startpunt geen evenwicht situatie kunnen bereiken (er is dan geen m die gemeenschappelijk is aan alle interagerende processen, dat betekent dat de processen dus niet als een som van getallen met enkel die m kunnen beschreven worden). Dus m selecteert een procesevenwicht, stabiliteit, invariantie voor interagerende processen, en het is dat wat we een Lorentz invariant noemen. Het is duidelijk dat m geen invloed heeft op de intensiteit van de schaalfactor vij+m, enkel op de eenheid van de schaalfactor. Voor een positieve m is die eenheid (“de tijd parameter”) groter dan de eenheid bij m=0. Voor een negatieve m is die eenheid (“de tijd parameter”) kleiner dan de eenheid bij m=0. We hebben daarenboven aangetoond dat er altijd een m zal kunnen gevonden worden die zelfs geen impact heeft op de intensiteit van de versnelling van het proces. Dit betekent dat we altijd processen kunnen vinden die niet versneld zijn, zoals de iconische “vrije val” en die kunnen dan gekarakteriseerd worden door een “tijdsrek” of “tijdskrimp” ten opzichte van de unieke situatie van m=0. Want er moeten dan ook processen zijn waarbij m enkel maar de waarde nul kan hebben wat dus ook overeenkomt met één welbepaald evenwicht punt. In dit standpunt zijn er geen toestanden (m=0) die geen verschil maken, “alles verandert en alle verandering is relevant”. Een nul is onvermijdelijk verbonden met een waarnemingsresolutie en de onmogelijkheid van ordening (waarneembaar klein en onwaarneembaar kleiner). We herinneren er aan dat we hebben aangetoond dat men een eenheid gelijk aan nul niet kan kiezen voor de schaalfactor eigen aan elk van de drie processen in evenwicht. Als we de basisrelaties bereiken door m=0 te stellen dan is deze m zeker niet de eenheid e van de schaalfactor, die eenheid e moet immers voldoen aan e2=1 om ervoor te zorgen dat (1+e2v01+mv12+m)=(1+v01+mv12+m). De uitspraak “alles verandert en alle verandering is relevant” betekent dus dat er geen ordening te maken is, er is geen stap die kleiner of groter is dan een andere, de veranderende tijd kan in ruimtetermen niet beschreven worden zodanig dat we zelfs niet in staat zijn om te oordelen dat de tijd toeneemt (of afneemt). Hetzelfde geldt voor de veranderende ruimte. De uitspraak “alles verandert en alle verandering is relevant” kan dan als “willekeurige verandering, ongeordende verandering” geïnterpreteerd worden.
De eenheid van m is dus algemener (meer abstract) dan e want m kan gelijk welke structuur of getal zijn maar e kan enkel maar gelijk zijn aan 1 (of -1).
Om de relatie tussen m (verschillend van nul) en e te onderzoeken beschouwen we de verhouding 1/γ12+mγ21+m=4(m+n1)(m+n2)/(2m+n1+n2)2=1-v212+m. Als ni willekeurige getallen zijn en als m een willekeurig getal is verschillend van nul, kunnen we teller en noemer van 1/γ12+mγ21+m delen door m2 en 1/γ12+mγ21+m schrijven we dan als 4(1+n1/m)(1+n2/m)/(1+n1/m+1+n2/m)2. De getallen ni zijn dan allemaal door hetzelfde getal gedeeld en ni/m komt dan overeen met de intensiteit van de veronderstelling van een lokale resolutie 1/m. Die 1/m, met als enige beperking dat m verschillend is van nul, kunnen we dan gebruiken als e. We kunnen dan alle getallen (m+ni) wegen met m. We krijgen dan nieuwe getallen (m+ni)/m waarin de intensiteit (m+ni) is en de eenheid 1/m. Noem deze getallen ki. Dat zijn dus intensiteiten (tellers) van de kleinste resolutie (gemeenschappelijke noemer 1/m). Dus (m+ni)/m=ki. Dus 1+ni/m=ki. Dat is niet anders dan dat we ni/m gelijkstellen aan ki-1. Dan is 1/γ12+mγ21+m niet anders dan 4k1k2/(k1+k2)2. Dit herkennen we als het patroon van een eigen ij-tijd maar dan met getallen ki. Deze verhouding is gelijk aan 1 wanneer alle ki dezelfde waarde hebben en dat komt overeen met v12+m gelijk aan nul en dus geen procesevenwicht maar een lokale intensiteit. Aangezien k1 en k2 positieve getallen zijn kunnen we 4k1k2/(k1+k2)2 ook interpreteren als een 1-w212 waarbij alle getallen ni/m die een toestand kwantificeren (en als intensiteiten van de eenheid 1/m gelezen worden) vervangen zijn door getallen (ki-1).
Het resultaat van deze inzichten is dat we nu kunnen modelleren dat we voor alle intensiteiten van toestanden dezelfde referentietoestand nemen en dat deze voorgesteld wordt door m=1 en dus niet door m=0. De reeks ki stellen we dus eigenlijk voor als (1+ni), dus (1+n0), (1+n1), (1+n2), … Van deze reeks is de maximale lokale resolutie dus 1. En dat geldt zowel als de eenheid van de ni positief is (“+1”) als negatief is (“-1”). In het eerste geval is ki=(m+ni)/m groter dan 1, in het tweede geval is ki=(m+ni)/m kleiner dan 1 en groter dan nul en als we de eenheid van ni expliciet willen tonen dan kunnen we dit schrijven als ki=(m-ni)/1 of als ki=(m+ni)/1. Dus ki is niet anders dan de 1-splitsing (1, κi) waarbij κi positief of negatief kan zijn maar altijd kleiner of gelijk aan 1 en verschillend van nul.
De eenheden m (hier verondersteld als +1) en e (ofwel (+1), ofwel (-1)) zijn dus invarianten voor elkaar en dat wordt duidelijk door de reeks (1+n0), (1+n1), (1+n2), …. De eenheid van het eerste getal (namelijk 1) uit de som (1+ni) is anders dan de eenheid van het tweede getal (namelijk ni). Hier zien we dus het verschil tussen het getal 2 en de 1-splitsing (1, 1).
Als we voor m nu een structuur nemen van het type 1+m’ dan kunnen we zeker voldoen aan de invariante keuze aangezien we voor e geen structuur gekozen hebben. Dan is 1+m’+e de manier van voorstellen, en dus te schrijven als het dubbelgetal 1+(m’+e).