De metrische afstand tussen een welgevormde haakuitdrukking en een welgevormde haakuitdrukking op centraal niveau is altijd in één dimensie uit te drukken. De metrische afstand tussen twee willekeurige welgevormde haakuitdrukkingen is altijd in twee dimensies uit te drukken. Dit is het duidelijkst te bewijzen door de haakuitdrukkingen binair voor te stellen. De twee dimensies moeten niet geometrisch geïnterpreteerd worden en volgen enkel uit de driehoeksongelijkheid. In de geometrische interpretatie kunnen we spreken van “een oppervlak”. De binaire metriek is goed gedefinieerd voor gelijk welk aantal bits en kan uitgebreid worden voor niet welgevormde haakuitdrukkingen. Aan “een oppervlak” of aan “twee dimensies” valt dus niet te ontsnappen. We zullen nu aantonen dat de metriek in een tralie ook als de metriek op een boloppervlak te begrijpen is.

Te bewijzen: elke tralie is op een driedimensionaal boloppervlak af te beelden

Bewijs

Het bewijs volgt eenvoudig uit de binaire voorstelling van een welgevormde haakuitdrukking. Elk (stand)punt in de tralie heeft hetzelfde aantal punten op afstand 1. Dit zelfde aantal (2ⁿ) wordt gegeven door het aantal bits waarmee de tralie opgespannen wordt. Er zijn dus punten op afstand 1 van het standpunt, op afstand 2, op afstand 3 enz… De inbedding van het standpunt ligt dus op maximale afstand, wat uiteraard enkel afhankelijk is van de grootte van het onderscheidingen universum, en er is zo maar 1 punt.

Elk punt in de tralie kunnen we dus beschouwen als het centrum van een aantal cirkels met toenemende straal tot het niveau bereikt is waar er evenveel hoogbits zijn als laagbits. Het grootste aantal punten bevindt zich op dat (centraal) niveau. De maximale afstand in de tralie wordt gegeven door de afstand tussen ingebedde punten en de punten op centraal niveau bevinden zich even ver van de punten die zich op maximale afstand bevinden. Het centraal niveau is het enige niveau waarop zich punten bevinden die elkaars inbedding zijn.

Het oppervlak dat deze metrische afbeelding mogelijk maakt is een boloppervlak.

QED

Op een boloppervlak onderscheiden we grote cirkels (“grootcirkels”) en cirkels die kleiner kunnen zijn dan grootcirkels. De grootcirkels zijn cirkels op een vlak door het centrum van de bol, de andere cirkel zijn cirkels op een vlak dat het centrum van de bol niet bevat. De kortste afstand tussen twee punten op de bol, gemeten op de bol, is dus deel van een grootcirkel en is dus gekromd, de kromming kunnen we kwantificeren door 1/R met R de straal van de betrokken cirkel die in dit geval ook de straal is van de bol (een cirkel met kleinere straal heeft een grotere kromming). Die straal is fysisch niet te meten (de afstand die we meten bevindt zich onvermijdelijk op het boloppervlak). R is een berekening met maar één beperking: R kan niet nul zijn. R is een parameter die gekozen kan worden onafhankelijk van het aantal onderscheidingen van het opgespannen onderscheidingen universum. R kan dan de afstand tussen punten op het boloppervlak verschalen. Een onderscheidingen universum heeft 2exp2ⁿ punten en die zijn allemaal op een boloppervlak af te beelden. De verschaling maakt het mogelijk om een afstand tussen twee punten te bekomen die waarneembaar is.

Een universum zonder onderscheidingen kent enkel <<>> en <> en die zijn altijd op grootste afstand van elkaar verwijderd. Een universum met één onderscheiding kent vier punten waarbij twee punten zich op centraal niveau bevinden, diametraal over elkaar. Een twee-onderscheidingen universum is een netwerk met een beperkt aantal punten dat nog gemakkelijk kan getekend worden. We kunnen hiermee ook andere eigenschappen van deze afbeelding illustreren zoals in de tekening die volgt.

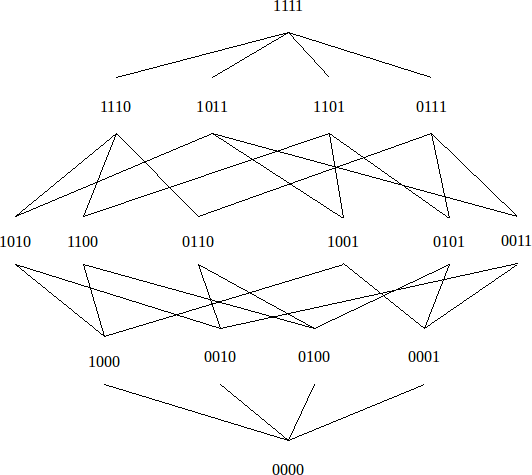
Dit is een voorstelling van de tralie van twee onderscheidingen. De lijnen tussen de 16 elementen geven de relatie van simultaneïteit van elk punt met punten op een niveau juist één hoger of juist één lager (wat we de "buren" van het punt noemen). De afstand tot deze buren is 1. Dit geeft onmiddellijk aan hoe misleidend het is om zich de bol met zijn boloppervlak voor te stelling als een fysische bol en een boloppervlak in drie dimensies: alle punten van een fysische bol sluiten elkaar uit en de relatie van simultaneïteit gaat dus verloren. Simultaneïteit (disjunctie, nevenschikking) is essentieel in het haakformalisme. Fysische dimensies kunnen naar hogere dimensies uitgebreid worden (zoals in de simplex reeks) maar blijven de karakteristieken van uitsluiting behouden. Dus ook in hogere dimensies krijgen we geen getrouwe afbeelding op een n-(hyper)-bol (hypersphere).

Een voorbeeld van punten die door een grootcirkel met elkaar verbonden zijn is: {1111, 1011, 1010, 0010, 0000, 0100, 0101, 1101}. Elk volgend punt bevindt zich op afstand 1 van het vorige punt en geen van de punten wordt tweemaal doorlopen. Een voorbeeld van punten die door een kleine bolcirkel met elkaar verbonden zijn is: {1101, 1011, 0111, 1110}. Zij bevinden zich allemaal op afstand 1 van 1111 (of op afstand 3 van 0000).

We merken op dat elk punt in een twee-onderscheidingen universum juist 4 onmiddellijk simultane buren heeft. We merken ook op dat elk punt zijn uniek symmetrische inbedding heeft. Het wordt gekarakteriseerd doordat de transformatie van de beide punten het punt 1111 geeft.

We beelden nu deze symmetrische punten diametraal tegenover elkaar af op een boloppervlak. We kunnen ze verbonden denken met een as door het centrum van de bol. In een twee-onderscheidingen universum zijn er zo 8 assen aangezien er 16 punten zijn.

De tralie voorstelling maakt het standpunt duidelijk van waaruit waargenomen wordt: 0000 en 1111 zijn de extrema en zijn dus het standpunt, wat te herkennen is door ze “niveau 0” en “niveau 4” te noemen.

Deze assen zijn in elkaar te roteren door een transformatie uit te voeren. Deze rotatie behoudt de hele structuur aangezien de transformatie van twee willekeurig gekozen punten een uniek derde punt oplevert. De tegengestelde rotatie bekomen we door de inbedding van een transformatie uit te voeren. De extrema in de nieuwe structuur zijn dan het nieuw standpunt van waaruit de structuur kan waargenomen worden.

In de volgende tabel is een transformatie uitgevoerd met <ab>.

Het getransformeerde standpunt wordt in onderstaande tralie weergegeven. Het is hiermee ook duidelijk dat de relatie van simultaneïteit ook veranderd is door dat standpunt in te nemen, de rol van <> in de definitie van de relatie wordt hier overgenomen door <ab>. Er zijn evenveel punten op afstand 1, 2, 3 en 4 van 1000 zoals er waren in de figuur met als supremum 1111.

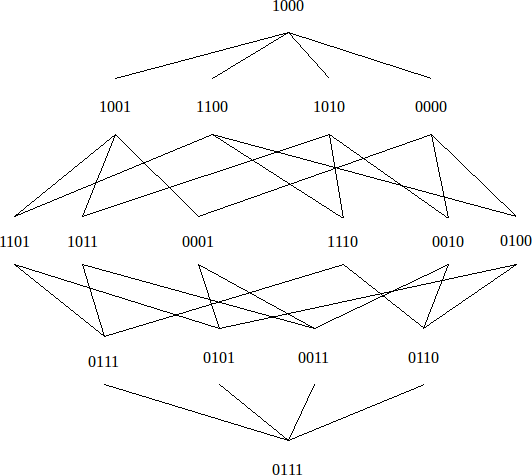
Dit maakt duidelijk dat elk punt dezelfde rol inneemt en dat dus enkel de structuur tussen de punten invariant is. Deze structuur is niet meer en niet minder dan het gevolg van het aantal buren, in dit voorbeeld is dit aantal vier. We moeten dus in het achterhoofd houden dat alle onderzoeken in die structuur op een vectorproduct na moeten geïnterpreteerd worden.

De binaire metriek in twee dimensies (die het gevolg is van de driehoeksongelijkheid) kwantificeert de oppervlakte van een boldriehoek zonder dat we daar geometrische interpretaties aan verbinden; het zijn schaalbare relaties. We kunnen de geometrie echter ook verder doortrekken door enkel punten te beschouwen die elkaar uitsluiten (waardoor we dus niet een volledige tralie modelleren) en dan blijkt dat we welgevormde haakuitdrukkingen op polytopen kunnen afbeelden waarvan de oppervlakken het duaal zijn van de punten.

Dit proces van afbeelding kan dus voor alle onderscheidingen universa uitgevoerd worden. Dus alle 2EXP2ⁿ punten van een n-onderscheidingen universum kunnen op een boloppervlak geprojecteerd worden waarbij de punten die elkaars inbedding zijn zich diametraal tegenover elkaar bevinden. Het aantal assen neemt exponentieel toe want het is gelijk aan 2EXP(2ⁿ-1). De afstand tussen de inbeddingen is de maximale afstand die in een universum mogelijk is, en komt overeen met de maximale afstand op het boloppervlak. Deze maximale afstand is te gebruiken om alle bollen tot een eenheidsbol te normaliseren, waarbij π een normalisatiefactor zal zijn. Elk punt heeft 2ⁿ buren op afstand 1, dus deze buren bevinden zich op een bolcirkel met het punt als “centrum op het boloppervlak”, raakpunt van een projectie. Elk punt kan als een standpunt gebruikt worden en is het centrum van verschillende bolcirkels met een straal met maat i. De kleinste cirkel heeft maat 1, de volgende heeft maat 2, de grootste cirkel heeft maat 2^n/2. Wanneer men zich nog verder verwijdert van het standpunt worden de cirkelstralen terug kleiner om bij de maximale afstand 2ⁿ bij de inbedding van het standpunt te belanden. Die bolcirkels bevinden zich op een vaste bolafstand van een pool van de bol (een standpunt) en bepalen dus een eerste hoek.

De grote cirkels op de bol beschrijven het pad van telkens één “niveaudiepte” vanuit een punt op de bol tot het diametraal tegengesteld punt op de bol. Er zijn zoveel grote cirkels als er punten zijn op centraal niveau. De grote cirkels maken het mogelijk om een tweede hoek te construeren.

Met deze twee hoeken kan de rotatie van het ene naar het andere standpunt gemodelleerd worden in twee stappen. Maar aangezien elke welgevormde haakuitdrukking in twee onderscheidingen kan uitgedrukt worden, kan daarmee ook één rotatiehoek bepaald worden door de constructie van één rotatie as.

Het is dus ook mogelijk om een afstand tussen welgevormde punten te definiëren, niet alleen door een binaire afbeelding maar ook met lengte (L), overeenkomend met een eerste hoek, en breedte (B), overeenkomend met een tweede hoek. Dit is de lengte en breedte zoals die gebruikt worden op een bol met straal R, overeenkomend met de coördinaten die gebruikt worden in het globaal coördinatensysteem op de Aarde. R wordt niet gemeten op het boloppervlak maar is een constructie die ons de notie van “kromming” kan suggereren zoals we die kennen voor een cirkel: een cirkel met grotere straal is minder gekromd dan een cirkel met kleine straal. De lengte kan overeenkomen met de afstand tussen twee aanliggende punten op eenzelfde niveau in de tralie en de breedte met de afstand tussen aanliggende simultane punten, op elk niveau één punt. We begrijpen vanuit een infinitesimale modellering van een afstand op een boloppervlak dat deze (infinitesimale!) afstand ook uit twee componenten bestaat zoals de binaire metriek in een tralie. Die infinitesimale afstand dS tussen welgevormde haakuitdrukkingen wordt dan gegeven door

dS²=R²dL²cos²B+R²dB² (0≤L<2π en -π/2≤B≤+π/2)

Dit is de formule die de infinitesimale afstand van de lange zijde van een rechthoekige driehoek op de bol dS relateert tot de infinitesimale breedte RdB en de infinitesimale lengte (RcosB)dL. Dit is snel als volgt in te zien: de breedte wordt gemeten aan een grote cirkel op de bol en de breedte is de centrale hoek, de lengte aan een cirkel met straal RcosB, de lengte is de hoek op het middelpunt van die cirkel. Uiteraard kan de formule dus driedimensionaal geometrisch afgeleid worden zie bijvoorbeeld blz56 uit Exploring Black Holes-2 van Edwin Taylor, John Archibald Wheeler en Edmund Bertschinger.

Het is belangrijk om in te zien dat we in staat zijn deze formule af te leiden enkel vanuit de veronderstelling van de tweedimensionale concepten “cirkel” of “hoek” en een hoek is niet anders dan een verhouding met een gekozen resolutie. Immers: veronderstel a²+b²-c² =0 als grens van een waarnemingsresolutie die we gebruiken om getallen te ordenen (nul is zeer klein en onwaarneembaar kleiner). Hieruit volgt: a²+b²=c² en c verschilt van nul. Dus er geldt ook: (a/c)²+(b/c)²=(c/c)². Tussen haken staan enkel verhoudingen (en dus schaalfactoren). Dus (a/c)²+(b/c)²=1 en dus is dit een benadering met rationale getallen van (sinθ)²+(cosθ)²=1. Rationale getallen kunnen we kiezen, irrationale getallen kunnen enkel gebeuren. Die verhoudingen vinden we terug in een rechthoekige driehoek en het Pythagoras drietal (a, b en c) is altijd vanuit andere getallen te construeren. We hebben dus geen geometrische intuïties nodig, evenmin als het driedimensionaal concept “bol”. Die intuïties kunnen trouwens zeer misleidend zijn aangezien alle punten op een fysisch boloppervlak elkaar uitsluiten. Dat is niet zo voor alle punten van een tralie, maar slechts voor een selectie van die punten. De volledige tralie wordt op een boloppervlak afgebeeld en de straal van die bol is enkel een berekening die met geen enkele “ervaring op het oppervlak” kan overeenkomen. Het oppervlak is gekromd maar de kromming is niet een “kromming in een hogere fysische dimensie” maar een kromming die een willekeurige verschaling mogelijk maakt van een gekozen tralie. We zien dat goed bij de formule van een cirkel: de relatie a²+b²=c² van zojuist schrijven we nu als de meer herkenbare x²+y²=R² en dit toont dat de soort relatie tussen x en y (een cirkel relatie) niet verandert als we R variëren, het enige wat we doen is de cirkel verschalen.

De straal van de bol (de verschaling) kan onafhankelijk gekozen worden van het aantal dimensies, dimensies die we de naam “onderscheiding” kunnen geven, die we de naam “toestand” kunnen geven, maar die enkel gelijken op fysische dimensies als ze elkaar uitsluiten (hun conjunctie is onmogelijk en hun disjunctie is onvermijdelijk).

Wat hebben we dan wel nodig als we geen geometrische intuïties nodig hebben:

• we kunnen een invariante som hebben voor de eenheid (1 is niet anders dan een som (verschil) van twee kwadraten die genormaliseerd zijn tot een specifieke verhouding) in een modulo 4 benadering die dan getallen introduceert

• er zijn eenheden die we als infinitesimalen kunnen modelleren die een heel duidelijke interpretatie hebben in het haakformalisme

Een tralie in twee onderscheidingen kunnen we afbeelden op een hyper cube in vier dimensies. Dezelfde tralie hebben we nu ook afgebeeld op een boloppervlak zonder dat daarvoor een hypersphere nodig is, waarbij duidelijk wordt dat hogere onderscheidingen universa op dezelfde manier kunnen afgebeeld worden op een boloppervlak maar dat de twee hoeken die hiervoor nodig zijn een grotere resolutie zullen krijgen (een kleiner deel van de hoek π). De verhouding van infinitesimale afstand tot straal wordt dan gegeven door (dS/R)²=dL²cos²B+dB² (0≤L<2π en -π/2≤B≤+π/2). Dit maakt duidelijk dat er maar één beperking is: R kan niet nul zijn. Meer ingewikkelde structuren introduceren niet noodzakelijkerwijze meer onderscheidingen. Hogere (geometrische) dimensies kunnen hoe dan ook op een drie dimensionale structuur (een bol) afgebeeld worden, wat aangepast moet worden is de resolutie of de schaal die kwantificeerbaar is door R.

Heeft de bol “een binnen” en “een buiten”

Een bol of een andere gesloten vorm kunnen we ons gemakkelijk voorstellen in de fysische ruimte als een structuur met “een binnen” en “een buiten”, met een centrum en een omgeving. Het centrum (een singulariteit) bevindt zich halverwege twee diametraal tegenoverliggende punten op het oppervlak, punten die samen een rotatie as van de gesloten vorm bepalen. De gebieden “binnen” of “buiten” zijn enkel definieerbaar door een keuze van berekenbare (niet waarneembare) metriek (de “R”) zodanig dat het begrip “groter dan” of “kleiner dan” zinvol wordt. “Buiten” is groter dan R, “binnen” is kleiner dan R. Zoals we aantoonden is R is niet anders dan een factor die alle afstanden op het boloppervlak kan schalen. Hierdoor kunnen we R relateren met “een laatst toegevoegde onderscheiding” die onvermijdelijk onze resolutie als agens-in-context bepaalt. Dat plaatst “waarneembaar” ten opzichte van “onwaarneembaar”. Dat is fysisch ervaarbaar als de resolutie die we aankunnen om een verschil waar te nemen (“hoe groot is onze nul in deze context van waarnemen”). We kunnen ook vrij kiezen of we onszelf op die schaal als “binnen” of “buiten” veronderstellen. Dat is een relatief gegeven. Essentieel is het boloppervlak: de tralie die we kunnen opspannen, niet “het binnen” of “het buiten”. Essentieel aan een boloppervlak is dat het geen begin of einde heeft, het is een structuur zonder singulariteit, en dat in tegenstelling met “een binnen” ofwel “een buiten” die afhankelijk is van de singulariteit “centrum” ten opzichte van “iets anders dan een centrum”. Misschien kunnen we dan aanvaarden dat het irrelevant is of we ons verbeelden binnen een bol te zijn of buiten een bol. Misschien kunnen we dan waarderen dat het moeilijk is voor ons om ons iets anders in te beelden dat, als we ons buiten een bol bevinden, we ons in een ruimte bevinden die niet een grotere bol is waarin we dan “binnen” zijn, maar wat is het dan wel? Zijn er verbeelding en berekening mogelijk die daar uitsluitsel kunnen over geven? Of moeten we maar gewoon aanvaarden dat de geometrische intuïties ons niet meer van nut kunnen zijn om ons de abstractie van tralies voor te stellen, tralies die een veel abstracter model zijn voor onze werkelijkheid dan geometrische modellen?

Een bol als concept

We moeten het concept “bol” dus als een abstract model beschouwen. De conceptuele stap die met het haakformalisme moet genomen worden in de “logische” werkelijkheid van onderscheidingen kan dus vergeleken worden met de conceptuele stap die onze verre voorouders moesten nemen om hun praktische vaardigheid van navigeren te kunnen begrijpen. Zij waren er immers van overtuigd dat de aarde plat was en dat de vaste grond omringend was door een zee. Sommigen vonden de avonturiers die zich op zee waagden zeer onverantwoordelijk omdat ze ooit eens zouden “afvallen van de aarde” (wat dat dan ook mocht betekenen in de veronderstelling dat iemand dat ooit zou willen gecommuniceerd hebben). De vissers die die overtuiging deelden gingen dan nooit voor zeekapitein solliciteren (daarenboven een zeer lastig beroep omdat de opleiding zeer lang was en gedurfd: om de zekerheid van de kust volledig los te laten moesten die jonge mensen precieze metingen leren maken en ze moesten leren navigeren met die getalletjes). Maar de nog levende zeekapiteins hadden nog nooit de grens van de wereld tegengekomen (en volgens de critici betekende dat enkel dat ze nog leven omdat ze “er” nog niet afgevallen waren). De vaste aarde had een zeer grillige vorm en soms vond men op zee een kortere route tussen twee punten. Dus de kapiteins gingen ervan uit dat ze in cirkels rond de wereld konden varen, en dat waren dus platte cirkels, en ze waren dus op zoek naar een andere route (die misschien korter zou zijn) indien ze in een andere richting zouden vertrekken.

Maar stel je nu voor dat een bolleboos onder onze voorouders tijdens zijn opleiding voor zeekapitein een getal (namelijk R) zou gevonden hebben (in zijn verbeelding), getal dat een vaste verhouding uitdrukt in een door hem gefantaseerde relatie tussen alle voldoende precieze en concrete metingen ΔS, ΔL, ΔB van driehoeken op de zee die gemeten werden met als referentie de Poolster, metingen die hij beschikbaar kreeg tijdens zijn opleiding. Hij vraagt zich dan af: wat betekent dat getal en waarom kunnen we dat niet meten, enkel berekenen? Nu gebruiken we de terminologie uit de twintigste eeuw: die R begrijpen we als de enkel berekenbare (en verbeeldbare) afstand die niet nul kan zijn voor een bol. Hij vraagt zich dan af: waarom is de afstand ΔS afhankelijk van ΔB? Nu begrijpen we dat de gekozen coördinaten L en B impliciet twee polen op de bol veronderstellen en dat de breedte-afstand tussen twee grote cirkels met punten met dezelfde lengtecoördinaat aan de polen kleiner wordt. Wanneer hij die relatie voorlegt aan zijn leraars (met de gevoeligheden van leraars uit de 21^ste eeuw zou die “hij” minstens ook een “zij” moeten zijn), dan is hun eerste vraag om met die gegevens eens de rand van de wereld te berekenen, een afstand die toch voor elke kapitein levensbepalend is (en een afstand die … als de leraar eerlijk is ... toch een beetje schrikaanjagend is). De student slaagt daar niet in, en ook de leraars niet. Die laatste zijn daar natuurlijk niet verbaasd over (zelfs als ze al begrepen dat een boloppervlak geen rand heeft, ze konden niet aanvaarden dat dit een toepasselijk model voor de Aarde zou zijn). Leraren en studenten keren dan maar terug naar de orde van de dag, want dat werkt (natuurlijk zou een romantische geest hier het verhaal aan brijen dat die jonge zeekapitein zeer oud geworden is en veel betekend heeft voor de samenleving maar nooit begrepen werd en op een dag voorgoed verdween op zee… hij moet dus wel van de wereld afgevallen zijn).

Dit is natuurlijk een analogie om de nog abstractere dubbele metriek van het tralie aspect van het haakformalisme te begrijpen en de hoeken die dit introduceert. De volgende conceptuele stap die we dan moeten doen is om de “laatst toegevoegde onderscheiding” een dynamische plaats te geven in het verhaal. We moeten dus “ruimte maken” voor een dynamiek van niveaus in een tralie, voor bollen die groter en kleiner worden, trillen, uit het niets opduiken en weer verdwijnen enz… wat dan weer als een golfverschijnsel kan gemodelleerd worden, goed beseffend dat die tralie niet bestaat uit elkaar uitsluitende punten zoals op een fysisch oppervlak maar simultane relaties modelleert. We zullen, afhankelijk van onze definitie, enkel sommige geselecteerde punten op het oppervlak vinden die elkaar uitsluiten, ze zullen dat niet allemaal zijn.

Misschien kan dit vergeleken worden met de conceptuele moeilijkheden die we allemaal hebben om ons een vierdimensionale werkelijkheid voor te stellen (een 4-hypercube zoals we deden voor een twee onderscheidingen universum) waarvan sommigen spreken als een “gekromde ruimtetijd”. Misschien kan dit vergeleken worden met de conceptuele moeilijkheden die we allemaal hebben om ons een “variëteit” (“manifold”) voor te stellen. Een variëteit wordt voorgesteld door een aantal overlappende kaarten (zoals de vlakke kaarten die we kunnen gebruiken om het aardoppervlak voor te stellen). Het is duidelijk dat de Aarde niet op één enkele vlakke kaart voorgesteld zou kunnen worden. Er is hiervoor dus een atlas van kaarten nodig die zodanig weinig gedetailleerd is dat aanpalende kaarten elkaar kunnen overlappen zonder conflict. In het haakformalisme begrijpen we een vlakke kaart als een 1-splitsing. Nu kunnen we het verband zien met het aantal onderscheidingen die in een kaart gebruikt worden, wat ons een nieuwe manier geeft op hierover na te denken. Bijvoorbeeld sommige punten van de variëteit kunnen als punt van een universum met minder onderscheidingen voorgesteld worden (in het binair model zal zo’n punt hetzelfde patroon in een langere string herhalen). Dat punt modelleert dan “lokaal” een kleiner universum en dat kleiner universum kan groot genoeg zijn om kaarten met elkaar te laten overlappen. De manier om dat te vinden is om het punt uit te drukken als creatief product, dus als rotatie. Elke locatie heeft dan zijn eigen rotatie en eigen invariant universum.

Het model van een variëteit zal ontwerpers niet verbazen omdat ze geleerd hebben om niet slechts één standpunt in te nemen, ze zijn immers verplicht om met verschillende stakeholders rekening te houden als ze resultaat willen bereiken, zelfs met mogelijke toekomstige stakeholders met a priori onkenbare verlangens. Stakeholders nemen anders waar, begrijpen andere dingen, verwachten (anticiperen) andere dingen en ondernemen dus andere acties om die anticipaties waarneembaar te maken.

Misschien moeten we terugkeren naar de orde van de dag van ontwerpers, want dat werkt? (Natuurlijk zou een romantische geest hier het verhaal aan brijen dat we op die manier wel zeer oud zouden kunnen worden en veel zouden kunnen betekenen voor de samenleving maar nooit begrepen zouden worden en op een dag voorgoed zouden verdwijnen “in werkelijkheid”…).